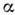к библиотеке к оглавлению FAQ по эфирной физике ТОЭЭ ТЭЦ ТПОИ ТИ

РЕАЛЬНАЯ ФИЗИКА

Глоссарий по физике

А Б В Г Д Е Ж З И К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Ю Я

Модель нуклонных ассоциаций

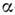Модель нуклонных ассоциаций - модель атомного ядра, основанная на представлении о ядре как о системе кластеров, или нуклонных ассоциаций, определённого типа, как правило,-кластеров. Простейший вариант Н. а. м. --кластерная модель - был сформулирован в 1937 Дж. А. Уиллером (J. A. Wheeler). Эксперпм. данные по энергиям связи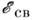 лёгких ядер указывают на повышенную энергию связи ядер с равным и чётным числом нейтронов (N)и протопов (Z): N = Z = 2п (п - целое число). 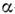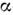Их можно считать состоящими из-частиц (-частичные ядра). К их числу относятся ядра ⁸Ве, ¹²С, ¹⁶O, ²⁰Ne и т. д. (п = 2, 3, 4, 5). В таких ядрах аномально велика энергия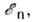 необходимая для отщепления (отделения) нейтрона; при переходе к соседнему нечётному по нейтронам ядру она уменьшается на 10 - 15 МэВ. В то же время энергия отделения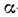-частицы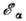мала. Так, ядро ⁸Ве не стабильно относительно распада на две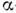-частицы, т. е.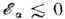 (строго говоря, такое ядро не существует), в ядре ¹²С энергия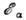 = 7 МэВ, в ¹⁶О 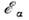= 16 МэВ. В разл. ядерных реакциях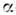-частичные ядра "охотно" испускают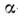-частицы. Среди возбуждённых состояний этих ядер есть состояния с аномально большими ширинами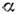 -переходов 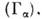близкими к т. н. вигнеровскому пределу; последний означает, что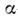-частицы на поверхности ядра существуют как "готовые". Перечисленные факты объясняются Н. а. м.
В Н. а. м. волновая функция ядра с массовым числом А = 4n представляется в виде антисимметризов. произведения п волновых функций 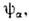описывающих внутр. движение нуклонов в отд.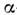-кластере, на волновую ф-цню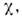 описывающую движение кластеров друг относительно друга. Напр., волновую функцию ядра ⁸Ве в Н. а. м. можно было бы записать в виде

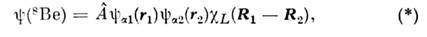
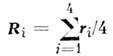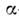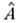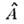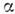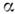где - радиус-вектор, определяющий положение центра тяжести-кластера, L - полный орбитальный момент ядра, - оператор антисимметризации по нуклонам, относящимся к разным кластерам. При замене оператора на 1 Н. а. м. переходит в простую-кластерную модель. При этом игнорируется внутр. структура-кластеров и описание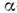-частичного ядра сводится к задаче совокупности п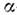-частиц с потенциалом взаимодействия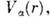 к-рый подбирается по фазам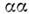-рассеяния. Такое приближение применимо для "рыхлых" систем, как, напр., ядро ⁸Ве, но не годится для более плотных ядер, как, напр., ¹⁶О. В случае ядра ¹²С волновая функция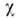 подчиняется Шрёдингера уравнению для системы трёх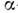-частиц.
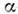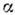В случае большего числа кластеров не существует простых точных методов решения ур-ния Шрёдингера. Чаще всего их находят, предполагая заданную конфигурацию для центров тяжести-кластеров, напр. равносторонний треугольник или цепочка (для 3-кластерного ядра ¹²С), правильный тетраэдр (для 4-кластерного ядра ¹⁶О). Параметры, определяющие данную конфигурацию, находятся минимизацией-кластерного гамильтониана.
Н. а. м. используется для описания ядерных реакций. Наиб. общим подходом здесь является т. н. метод резонирующих групп, в к-ром для описания рассеяния нуклонов на ядрах применяется волновая функция типа (*), а для описания реакций передачи одного или неск. нуклонов ядру - её обобщения. Упрощённые варианты Н. а. м. используются в теории альфа-распада ,а также для описания f-радиоактивности - спонтанного распада тяжёлых ядер с испусканием тяжёлых фрагментов (напр., ядер ¹⁴С, ²⁰Ne, см. Радиоактивность).
Метод, близкий к Н. а. м., - двуцентровая модель оболочек - используется для описания т. н. молекулярных состояний ядер (ядерных молекул). Такие состояния были обнаружены в лёгких ядрах. Напр., нек-рые состояния ядра ²⁴Mg интерпретируются как "молекула", состоящая из двух ядер ¹²С, находящихся на нек-ром расстоянии друг от друга. Ядерные молекулы описываются волновой функцией вида (*) с заменой 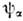на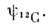
Получили распространение модели, исходящие из кваркового строения нуклона. В них нуклон рассматривается как 3-кварковый кластер и предполагается также существование мультикварковых конфигураций: 6- и 9-кварковых кластеров.
Представления Н. а. м. оказались полезными и для описания процесса фрагментации нуклонов в ядерных реакциях под воздействием тяжёлых ионов высоких энергий. В этих ядерных реакциях образуется составная ядерная система в виде нагретого и сжатого сгустка ядерного вещества (файрбол), к-рый, остывая, расширяется до плотности, примерно вдвое меньшей нормальной ядерной плотности. Ожидается, что при такой плотности увеличивается вероятность образования разл. кластеров, к-рые и испускаются в процессе распада составной системы.

Литература по модели нуклонных ассоциаций

Вильдермут К., Тан Я., Единая теория ядра, пер. с англ., М., 1980.

Э. Е. Саперштейн

к библиотеке к оглавлению FAQ по эфирной физике ТОЭЭ ТЭЦ ТПОИ ТИ

Знаете ли Вы, что низкочастотные электромагнитные волны частотой менее 100 КГц коренным образом отличаются от более высоких частот падением скорости электромагнитных волн пропорционально корню квадратному их частоты от 300 тысяч кмилометров в секунду при 100 кГц до примерно 7 тыс км/с при 50 Гц.

НОВОСТИ ФОРУМА

Рыцари теории эфира