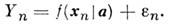
Метод наименьших квадратов - метод оценивания неизвестных параметров теоретич. моделей по косвенным измерениям при параметрич.
анализе данных (см. Анализ данных ).H. к. м. был предложен К. Гауссом
(С. GauB, 1809) для задач геодезии и астрономии в след. формулировке. Пусть
существует модель явления, в к-рой x - вектор аргументов,
а - вектор неизвестных параметров. Для определения параметров
а проводятся косвенные измерения, т. е. измеряются не сами
параметры a, a функции этих параметров f (х|а), вычисляемые согласно модели. Благодаря ошибкам измерения en
результаты измерения Yn равны
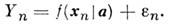
Относительно en предполагается,
что они являются чисто случайными величинами, т. е. при многократном проведении
измерений их ср. значения равны нулю, M(en) =
0, M(Yn) = f(xn|a), а также что они
некорре-лированы и их дисперсии равны s2n
, M(enem)= s2ndnm. Согласно Гауссу, в качестве оценки а (оценки H. к.
м.) следует взять величину а^, минимизирующую
выражение
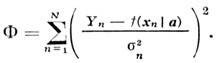
При этом подразумевается, что число измерений
N>=I, где I - число неизвестных параметров ai.
Обобщением метода на случай коррелиров. ошибок
измерения, M(enem)
= Snm,
является поиск величины 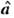 из условия минимума квадратичной формы
из условия минимума квадратичной формы
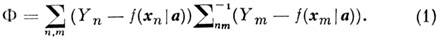
H. к. м. используют при обработке результатов
наблюдений, в разл. задачах регрессионного анализа и т. д. Напр., в физике элементарных частиц его применяют для оценки импульса частицы по измерениям
координат точек её траектории в магн. поле и оценки параметров плотности распределения
р(х|а)случайной величины c по числу событий
Yn в ячейках гистограммы.
Оптимальность оценки H. к. м. Использование
метода обусловлено оптим. свойствами его оценки для моделей с линейной зависимостью
M(Yn)= f(xn|a)от параметров
а. Рассмотрим их. Итак, пусть
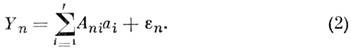
Выражение (1) в этом случае кратко записывается
в виде
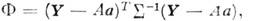
где T - символ транспонирования. В предположении,
что ранг матрицы А больше или равен I, оценка H. к. м. равна
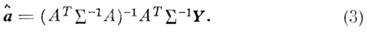
Из (3) следует, что 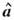 является линейной оценкой, т. е. линейной функцией измерений Yn. Если усреднить (3) по ошибкам измерения, то оказывается, что
является линейной оценкой, т. е. линейной функцией измерений Yn. Если усреднить (3) по ошибкам измерения, то оказывается, что
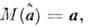
т. е. оценка является несмещённой.
Благодаря ошибкам измерения 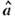 имеет шумовую составляющую, к-рая характеризуется матрицей ошибок (ковариационной
матрицей):
имеет шумовую составляющую, к-рая характеризуется матрицей ошибок (ковариационной
матрицей):
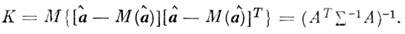
Диагональные элементы Кii являются
дисперсиями ошибок, содержащихся в 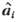 .
.
В исследование оптимальности H. к. м. внёс вклад
А. А. Марков, к-рый в 1900 доказал след. утверждение (теорема Гаусса - Маркова):
среди всех линейных несмещённых оценок минимальными дисперсиями Кii обладает оценка (3), т. е. оценка Н. к. м.
В том случае, когда S = s2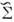 ,
где s2 - неизвестный параметр,
,
где s2 - неизвестный параметр, 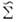 - известная матрица, несмещённой оценкой s2 является величина
- известная матрица, несмещённой оценкой s2 является величина
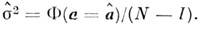
Величину N - I наз. числом степеней свободы.
Подчеркнём, что перечисленные оптим. свойства
оценки H. к. м. не зависят от вида распределения вектора e, а лишь
от предположения справедливости линейной связи (2).
Иногда оказывается, что между искомыми параметрами
аi существует связь, отражающая физ. закономерность:
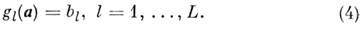
Напр., импульсы всех частиц в точке взаимодействия
удовлетворяют закону сохранения 4-импульса. Учёт такой априорной информации
приводит к уменьшению ошибок оценок параметров. Если связи (4) линейны, т. е.
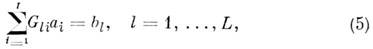
то оценка 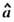 H. к. м., удовлетворяющая (5), имеет вид
H. к. м., удовлетворяющая (5), имеет вид
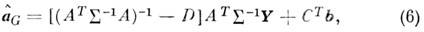
где
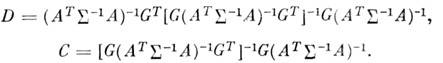
Можно убедиться, что оценка (6) является несмещённой,
а для её матрицы ошибок KG выполняется
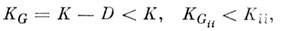
т. к. D - положительно определённая матрица.
В случае нелинейных связей (4) задача построения
оценки H. к. м., удовлетворяющей (4), существенно усложняется и решается численными
методами.
Разновидности H. к. м. Важным частным
случаем H. к. м. является c2-метод,
к-рый используется при работе с данными, сгруппированными в гистограмму. В этом
случае Yn есть числа событий в ячейках гистограммы. При больших
значениях Yn их можно рассматривать как независимые случайные
величины, распределённые по нормальному
закону. Если изучаемое распределение есть р(х|а), где x - измеряемая
случайная величина, а - вектор неизвестных параметров,
то ср. число событий в ячейке гистограммы 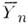 (а)
равно
(а)
равно 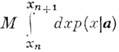 (M - полное число событий), а дисперсия
Yn равна
(M - полное число событий), а дисперсия
Yn равна 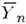 (а). Тогда, согласно H. к. м., оценка а должна находиться
из минимума выражения
(а). Тогда, согласно H. к. м., оценка а должна находиться
из минимума выражения
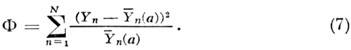
Для упрощения задачи минимизации (7) 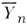 (а)
в знаменателе (7) часто заменяют на Yn (модифицированный c2-метод).
Своё назв. метод получил по той причине, что при больших Yn (приближение
нормального распределения) Ф(а =
(а)
в знаменателе (7) часто заменяют на Yn (модифицированный c2-метод).
Своё назв. метод получил по той причине, что при больших Yn (приближение
нормального распределения) Ф(а = 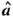 )
распределено по c2-pаспрe-делению
с числом степеней свободы N - I - 1.
)
распределено по c2-pаспрe-делению
с числом степеней свободы N - I - 1.
Если функции f(x|a)или р(х|а)нелинейны, то поиск оценки а осуществляется одним из
методов численной минимизации (1) или (7). Тем не менее можно получить ряд асимптотич.
свойств (при N 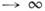 ) оценки H. к. м.
) оценки H. к. м.
Оценка H. к. м. состоятельна, т. е. при N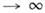 один из корней системы ур-ний дФ/дai = 0 сходится к точному
значению а. Оценка H. к. м. асимптотически распределена
по нормальному закону. Однако матрица ошибок
один из корней системы ур-ний дФ/дai = 0 сходится к точному
значению а. Оценка H. к. м. асимптотически распределена
по нормальному закону. Однако матрица ошибок  больше обратной к информац. матрице (см. Максимального правдоподобия метод), т. е. оценка H. к. м. не является эффективной. При конечных N оценка
H. к. м. является смещённой и неэффективной. Эфф. способом изучения её свойств
является Монте-Карло метод: задаваясь значением а из
области возможных значений, получают выборку Yn; по Yn находят оценку
больше обратной к информац. матрице (см. Максимального правдоподобия метод), т. е. оценка H. к. м. не является эффективной. При конечных N оценка
H. к. м. является смещённой и неэффективной. Эфф. способом изучения её свойств
является Монте-Карло метод: задаваясь значением а из
области возможных значений, получают выборку Yn; по Yn находят оценку 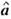 и строят выборочные среднее
и строят выборочные среднее 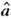 и матрицу ошибок (вообще говоря, выборочное распределение). Отметим, что на
практике широко используют приближённое выражение для матрицы ошибок
и матрицу ошибок (вообще говоря, выборочное распределение). Отметим, что на
практике широко используют приближённое выражение для матрицы ошибок
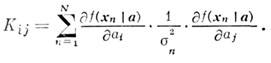
В том частном случае, когда распределение Yn является многомерным нормальным распределением, кова-риац. матрица к-рого
не зависит от a, H. к. м. совпадает с методом макс. правдоподобия.
В этом случае оценка H. к. м. обладает оптим. свойствами, присущими оценке максимума
правдоподобия. Кроме того, F(a = 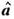 )
распределено по c2-распределению
с числом степеней свободы N - I.
)
распределено по c2-распределению
с числом степеней свободы N - I.
Для нелинейных f(x|a)и р(х|а)широкое использование H. к. м. обусловлено двумя причинами: 1) метод не требует знания функции распределения Yn, а лишь среднего M(Yn) = f(xn|a)и матрицы ошибок S; 2) задача минимизации квадратичных форм (1) и (7) значительно проще задачи минимизации функций более общего вида, к-рые появляются в др. методах оценивания.

В. П. Жигунов, С. В. Клименко
|
|