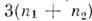 - 6 независимых переменных. При рассмотрении M. в. достаточно сложных молекул
возникает задача нахождения на многомерной потенц. поверхности глобальных экстремумов
среди большого числа локальных, связанных с перемещением и деформацией молекул.
- 6 независимых переменных. При рассмотрении M. в. достаточно сложных молекул
возникает задача нахождения на многомерной потенц. поверхности глобальных экстремумов
среди большого числа локальных, связанных с перемещением и деформацией молекул.По природе, характерным энергиям и расстояниям близко к межатомному взаимодействию. Описывается теми же типами потенциалов
взаимодействия, что и межатомное взаимодействие. M. в. наиб, существенно в плотных
газах и молекулярных конденспров. телах, т. е. в тех случаях, когда существуют
индивидуальные молекулы. Не имеет смысла говорить о M. в. в металлах, ионных
кристаллах, их растворах и расплавах.
В результате M. в. происходят изменения в окружающей
среде, под влиянием к-рых искажаются электронные оболочки и взаимное расположение
атомов, входящих во взаимодействующие молекулы. По существу, M. в. сводится
к совокупности взаимодействий каждого из атомов одной молекулы с каждым из атомов
другой с учётом воздействия окружающей среды. M. в. обусловлено перекрыванием
внеш. электронных оболочек атомов. Потенциалы M. в. часто выражаются аддитивными
комбинациями атом-атомных, атом-ионных, ионно-ионных парных потенциалов. Однако
принцип аддитивности справедлив лишь для эл--статич. взаимодействий, ограниченно
применим для дисперсионных и неприменим к индукционным, резонансным и обменным
M. в.
Описание взаимного расположения молекул требует
введения огромного числа координат, что преобразует одномерные (изотропные,
сферически симметричные) зависимости потенц. энергии от координат (имеющие место,
напр., для атом-атомного парного взаимодействия) в многомерные потенциальные
поверхности M. в. В частности, для описания M. в. двухатомных молекул нужно
ввести 6 параметров: расстояние между центрами молекул, два угла между осями
молекул и линией, соединяющей их центры, угол между плоскостями, в к-рых лежат
линия центров и каждая молекула, а также два межъядерных расстояния молекул.
При M. в. двух молекул, состоящих из п1 и п2 атомов, их потенциал з-ависит от 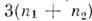 - 6 независимых переменных. При рассмотрении M. в. достаточно сложных молекул
возникает задача нахождения на многомерной потенц. поверхности глобальных экстремумов
среди большого числа локальных, связанных с перемещением и деформацией молекул.
- 6 независимых переменных. При рассмотрении M. в. достаточно сложных молекул
возникает задача нахождения на многомерной потенц. поверхности глобальных экстремумов
среди большого числа локальных, связанных с перемещением и деформацией молекул.
Атомы в каждой из взаимодействующих молекул удерживаются
хим. связями, a M. в. осуществляется более слабыми силами - ваи-дер-ваальсовыми
(рис. 1) или водородными связями. В жидкостях и газах за счёт
водородных связей молекулы образуются кластеры и полимеры ,в молекулярных
кристаллах - цепочки, сетки и сверхрешётки.
За межмолекулярное расстояние принимают расстояние между ядрами ближайших атомов
взаимодействующих молекул; они обычно больше характерных длин хим. связей. Молекулы
как бы одеты в "шубу" (рис. 2), толщина к-рой равна радиусу  M. в. В табл. приведены (в
M. в. В табл. приведены (в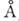 )
атомные
)
атомные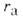 и молекулярные
rм радиусы нек-рых атомов (у благородных газов
и молекулярные
rм радиусы нек-рых атомов (у благородных газов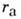 и
и
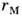 совпадают).
совпадают).

Анизотропия M. в. M. в. зависят от направления,
т. е. анизотропны. Наиб, яркое макроскопич. проявление анизотропии M. в.- образование
кристаллич. и жид-кокристаллич. структур. Анизотропия M. в. проявляется также
в обмене энергией между разл. степенями свободы молекул, что приводит к стационарному
(но не
равновесному) сосуществованию значительно различающихся
поступательной (и примерно равной ей вращательной), колебательной и электронной
энергий газовой смеси. Это явление используется при создании лазеров, адекватной
оценки параметров хим. и плазмо-хпм. процессов, процессов переноса и т. п.
Ограниченная применимость моделей разл. сферически-симметричных
(одномерных) потенциалов связана с тем, что центральное M. в. не может изменить
угл. момент и нек-рые компоненты колебат. движения молекул.
Анизотропия M. в.- следствие несимметричного
распределения электрич. зарядов молекулы, т. е. возникновения мультипольных
моментов и анизотропии дисперсионного и обменного взаимодействий. Кроме того,
даже при относительно-симметричном расположении зарядов анизотропия возникает
в результате несовпадения центра зарядов с центром тяжести молекулы. На рис.
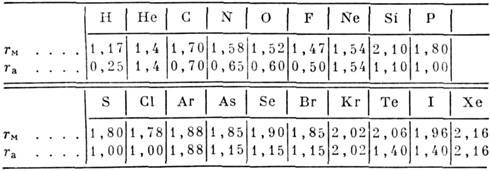
3 приведены зависимости потенциалов M. в. от радиуса r при разл. взаимном расположении молекул водорода и атомов гелия.
Рис. 3. Потенциалы взаимодействия Hc(2aS)
с молекулами водорода. Пунктирная кривая получена в экспериментах по рассеянию
молекулярных пучков в сферически-симметричной апроксимации. Теоретические кривые
(сплошные) получены для различных взаимных расположений атомов Не(·) и молекул
водорода (·-·).
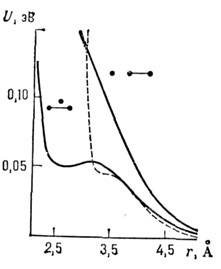
Рис. 4. Взаимное расположение атома А и
молекулы BC, при к-ром возникает анизотропное межмолекулярное взаимодействие;
D - центр молекулы BC; v - угол между осью молекулы и направлением
AD.
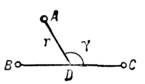
Анизотропные потенциалы можно представить в виде
разложения по полиномам Лежандра. M. в. атома А с молекулой BC (рис. 4) описывается
потенциалом где -
радиальные
-
радиальные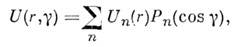 компоненты,
Pn - полиномы Лежандра
(угол g отмечен на рис.). Ограничиваясь чётными компонентами для первых
двух членов, можно получить для U0 и U0
выражения в виде потенциала Леннарда-Джонса:
компоненты,
Pn - полиномы Лежандра
(угол g отмечен на рис.). Ограничиваясь чётными компонентами для первых
двух членов, можно получить для U0 и U0
выражения в виде потенциала Леннарда-Джонса:
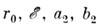 -
-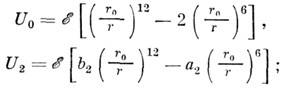
оптимальные для данной системы подгоночные
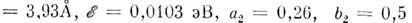 .
.
параметры: для системы, напр., 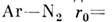
M. в. в жидкостях. Независимо от свойств
среды два эквивалентных объекта (пузырьки или коллоидные частицы) всегда притягиваются
друг к другу. В том /ко случае, когда диэлектрич. восприимчивости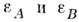 взаимодействующих молекул А и В и молекул среды
взаимодействующих молекул А и В и молекул среды 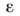 отвечают неравенству
отвечают неравенству 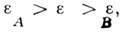 молекулы А и В отталкиваются.
молекулы А и В отталкиваются.
Сила взаимодействия двух противоположных но знаку
и равных по величине зарядов, между к-рыми расположена поляризующаяся сферич.
область (рис. 5, а), равна
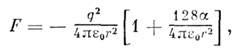
где  -
поляризуемость
-
поляризуемость
среды,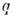 -
абс. величина каждого из зарядов, r - расстояние между ними,
-
абс. величина каждого из зарядов, r - расстояние между ними, 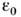 - диэлектрич. проницаемость вакуума. T. о., наличие поляризующейся среды между
молекулами
- диэлектрич. проницаемость вакуума. T. о., наличие поляризующейся среды между
молекулами
Рис. 5. Различное расположение зарядов +q
и -q сферических поляризующихся областей r - расстояние между
зарядами; d - расстояние между зарядами и центрами сферических областей.
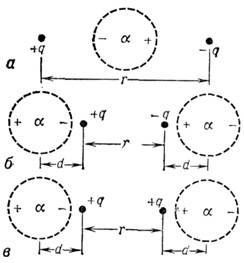
увеличивает их потенц. энергию взаимодействия.
Для зарядов, расположенных, как показано на рис. 5(б), сила
взаимодействия уменьшается:
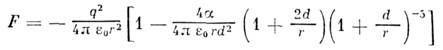
(d -расстояние между зарядами и центрами
сферич. областей).
Для случая, когда заряды имеют одинаковый знак
(рис. 5, в),

Дисперсионная энергия взаимодействия (см. Межатомное
взаимодействие)может быть вычислена с помощью теории возмущений. В более
общем виде многочастичная задача M. в. решается при рассмотрении M. в. во флуктуирующем
эл--магн. поле в непрерывной среде, характеризуемой комплексной диэлектрич.
проницаемостью, зависящей от частоты поля.
Влияние магнитного поля на M. в. Теоретически
предсказано и экспериментально обнаружено, что M. в. изменяется (возрастает)
под действием не слишком интенсивных магн. полей, что приводит к увеличению
(на десятки и сотни процентов) скоростей хим. превращений. В результате возникла
новая область - спиновая химия. Обнаруженные явления основаны на законе Вигнера
- сохранении электронного спина и влиянии магн. поля на интеркомбинац. переходы
между разл. спиновыми состояниями взаимодействующих молекул.
Аналитические методы расчёта M. в. Для расчёта потенциалов M. в. разработано большое число эмпи-рич., полуэмпирич.
и чисто теоретич. (квантовомеха-нич.) методов. Обычно расчёты очень трудоёмки
и осуществляются на ЭВМ. Основной из них - метод самосогласованного поля (метод
Хартри - Фока) и линейной комбинации молекулярных орбиталой (см. Квантовая
химия). При выполнении аддитивности электронных плотностей взаимодействующих
фрагментов применим метод модели электронного газа с использованием функционала
Томаса - Ферми - Дирака.
Достаточно распространённой задачей является
расчёт M. в. двух длинных насыщенных молекулярных цепей, к-рые часто состоят
из чередующихся однотипных фрагментов с однотипным распределением зарядов
в каждом из них. В качестве фрагментов могут рассматриваться и отд. атомы либо
пары химически связанных молекул. Используя второе приближение теории возмущений,
можно рассчитать дисперсионное взаимодействие двух параллельных цепных молекул.
Если две одинаковые молекулы состоят из N одинаковых фрагментов, каждый
из к-рых взаимодействует с фрагментом др. молекулы, находящимся от него на расстоянии
r, то энергия взаимодействия U(r)равна

что справедливо, если 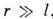 ,
где l - размер фрагмента, С -
константа. Суммарная энергия взаимодействия молекул длиной L, расположенных
на расстоянии R друг от друга, равна
,
где l - размер фрагмента, С -
константа. Суммарная энергия взаимодействия молекул длиной L, расположенных
на расстоянии R друг от друга, равна

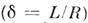 .
.
В двух предельных случаях больших и малых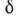 соответственно
имеем:
соответственно
имеем:

и
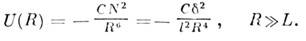
Используя приближённую ф-лу для дисперсионной
энергии взаимодействия связей, получим
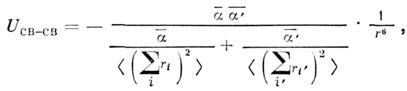
где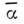 -
ср. поляризуемость связи,
-
ср. поляризуемость связи, 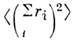 квантовомеханич. среднее квадрата суммы электронных координат связи с началом
координат в центре тяжести электронного облака. Ниже приведены результаты расчётов
(с точностью ~ 30%) дисперсионной константы С (в а. е. м.) взаимодействия
связей в углеводородных веществах.
квантовомеханич. среднее квадрата суммы электронных координат связи с началом
координат в центре тяжести электронного облака. Ниже приведены результаты расчётов
(с точностью ~ 30%) дисперсионной константы С (в а. е. м.) взаимодействия
связей в углеводородных веществах.

Вычисление суммарной энергии взаимодействия,
напр, двух структурных единиц CH2, приводит к выражению
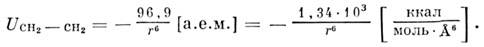
Аналогичные вычисления выполнены и для др. атом-атомных потенциалов.

Ю. H. Любитов
Когда тот или иной физик использует понятие "физический вакуум", он либо не понимает абсурдности этого термина, либо лукавит, являясь скрытым или явным приверженцем релятивистской идеологии.
Понять абсурдность этого понятия легче всего обратившись к истокам его возникновения. Рождено оно было Полем Дираком в 1930-х, когда стало ясно, что отрицание эфира в чистом виде, как это делал великий математик, но посредственный физик Анри Пуанкаре, уже нельзя. Слишком много фактов противоречит этому.
Для защиты релятивизма Поль Дирак ввел афизическое и алогичное понятие отрицательной энергии, а затем и существование "моря" двух компенсирующих друг друга энергий в вакууме - положительной и отрицательной, а также "моря" компенсирующих друг друга частиц - виртуальных (то есть кажущихся) электронов и позитронов в вакууме.
Однако такая постановка является внутренне противоречивой (виртуальные частицы ненаблюдаемы и их по произволу можно считать в одном случае отсутствующими, а в другом - присутствующими) и противоречащей релятивизму (то есть отрицанию эфира, так как при наличии таких частиц в вакууме релятивизм уже просто невозможен). Подробнее читайте в FAQ по эфирной физике.
|
|