В основе методов определения масс небесных тел лежит всемирного тяготения закон .В астрономии
часто (но не всегда) можно пренебречь размерами небесных тел по сравнению с
разделяющими их расстояниями и отличием их формы от точной сферы, т. е. уподобить
небесные тела точечным массам.
Масса Земли может быть определена по величине
ускорения свободного падения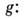
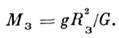
Величина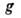 определяется
гравиметрич. методами (см. Гравиметр, Гравиметрия), a R3 -
на основе геодезич. измерений. Таким путём найдено, что масса Земли
определяется
гравиметрич. методами (см. Гравиметр, Гравиметрия), a R3 -
на основе геодезич. измерений. Таким путём найдено, что масса Земли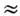
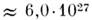 г. Более точно M3 (вернее, произведение GМз)определяется
по наблюдениям ИСЗ или космич. аппаратов. Помимо массы Земли, прямым гравиметрич.
методом измерения силы тяжести на поверхности небесного тела можно определить
массу Луны, а в дальнейшем всех планет и их спутников с твёрдой поверхностью.
г. Более точно M3 (вернее, произведение GМз)определяется
по наблюдениям ИСЗ или космич. аппаратов. Помимо массы Земли, прямым гравиметрич.
методом измерения силы тяжести на поверхности небесного тела можно определить
массу Луны, а в дальнейшем всех планет и их спутников с твёрдой поверхностью.
Определение массы Земли является первым звеном
в цепи определений масс др. небесных тел (Луны, планет, Солнца, а затем и др.
звёзд). Массы этих тел находят, опираясь либо на 3-й закон Кеплера (см. Кеплера
законы), либо на след, правило: расстояния к--л. масс от общего центра масс
обратно пропорциональны самим массам. Это правило позволяет, в частности, определить
массу Луны. Отношение расстояний центров Луны и Земли от центра масс система
Земля - Луна (барицентра) равно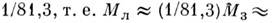
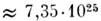 г.
г.
Массу Солнца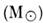 можно
определить, применив 3-й
можно
определить, применив 3-й
закон Кеплера к движению Земли (вместе с Луной)
вокруг Солнца и к движению Луны вокруг Земли:
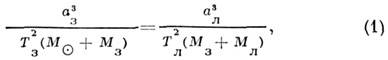
где а - большие полуоси орбит, T -
периоды (звёздные, или сидерические) обращения. Если пренебречь массой Земли
по сравнению с массой Солнца, то отношение 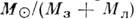 оказывается равным 329390, отсюда
оказывается равным 329390, отсюда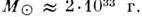
Ф-ла (1) даёт возможность сравнить массы Солнца
и любой планеты, имеющей спутник, или массы двух планет, имеющих спутники. Массы
планет, у к-рых нет спутников, определяют по возмущениям, оказываемым ими на
движение соседних планет.
Массу звезды (помимо Солнца) можно определить
со сравнительно большой надёжностью только в том случае, если она является физ.
компонентом визуально-двойной звезды (см. Двойные звёзды ),расстояние
до к-рой известно. 3-й закон Кеплера в этом случае
даёт сумму масс компонентов (в единицах солнечной
массы):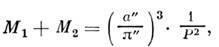
где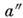 -
большая полуось (в секундах дуги) относительной орбиты спутника вокруг главной
(обычно более яркой) звезды, к-рую в этом случае считают неподвижной; P -
период обращения в годах;
-
большая полуось (в секундах дуги) относительной орбиты спутника вокруг главной
(обычно более яркой) звезды, к-рую в этом случае считают неподвижной; P -
период обращения в годах;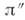 -
параллакс системы (в секундах дуги). Величина
-
параллакс системы (в секундах дуги). Величина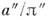 даёт значение большой полуоси орбиты в а. е. Если можно измерить угл. расстояния
даёт значение большой полуоси орбиты в а. е. Если можно измерить угл. расстояния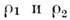 компонентов
компонентов
от общего центра масс [напр., по положению каждого
компонента относительно несколько более слабых звёзд (звёзд фона) или в случае
заметного собств. движения центра масс, как у Сириуса и его спутника], то находят
отношение масс,  ,
и, следо-
,
и, следо-
вательно, массу каждой звезды в отдельности.
Для определения малых значений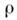 у
тесных двойных звёзд успешно применяются методы спекл-интер-ферометрии. Если компоненты двойной имеют примерно одинаковый блеск и сходные спектры,
то полусумма масс даёт достаточно надёжную оценку массы каждого компонента и
без дополнит, определения отношения
у
тесных двойных звёзд успешно применяются методы спекл-интер-ферометрии. Если компоненты двойной имеют примерно одинаковый блеск и сходные спектры,
то полусумма масс даёт достаточно надёжную оценку массы каждого компонента и
без дополнит, определения отношения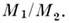
Для др. типов двойных звёзд (затменно-двойных
и спектрально-двойных) имеется ряд возможностей приблизительно определить массы
звёзд или оценить их ниж. предел.
Совокупность данных о массах компонентов более
чем сотни двойных звезд разных типов позволила обнаружить важную статистич.
масса - светимость зависимость. На основе этой зависимости оценивают
массы одиночных звёзд по их светимостям.
Ещё один метод оценки массы звезды связан с измерением
гравитац. красного смещения спектральных линий в поле тяготения. В сферически
симметричном поле тяготения звезды оно эквивалентно доплеровскому красному смещению:
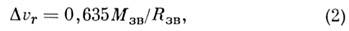
где М3B- масса звезды в единицах
массы Солнца, Rзв - радиус звезды в единицах радиуса Солнца,
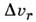 - в км/с. Соотношение
(2), наиб, успешно применяемое к белым карликам, проверено по ряду белых карликов,
входящих в состав двойных систем. Для них были известны радиусы, массы и истинные
лучевые скорости.
- в км/с. Соотношение
(2), наиб, успешно применяемое к белым карликам, проверено по ряду белых карликов,
входящих в состав двойных систем. Для них были известны радиусы, массы и истинные
лучевые скорости.
У т. н. астрометрич. двойных звёзд один компонент
невидим. Массу невидимого (тёмного) спутника звезды можно оценить по колебаниям
положения звезды, связанным с её движением около общего центра масс. Невидимые
спутники звёзд имеют массы меньше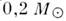 и, вероятно, похожи на планеты. Возможно, что вместо одного тёмного спутника
имеются два-три, а может быть, и большее число спутников (планет), т. е. планетные
системы.
и, вероятно, похожи на планеты. Возможно, что вместо одного тёмного спутника
имеются два-три, а может быть, и большее число спутников (планет), т. е. планетные
системы.
На релятивистском эффекте вращения линии апсид
орбиты звезды-компаньона (подобного эффекту вращения линии апсид планетарных
орбит, см. Тяготение)основан ещё один способ определения масс компонентов
двойной звезды.
Массы звёзд заключены в пределах прибл. от 0,03
до 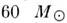 (теоретич.
предел стабильной массы нор-
(теоретич.
предел стабильной массы нор-
мальной звезды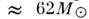 ).
Наиб, число звёзд имеет
).
Наиб, число звёзд имеет
массы от 0,3 до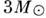 ,
много более половины звёзд вхо-
,
много более половины звёзд вхо-
дят в двойные системы. Cp. масса звезды в ближайших
окрестностях Солнца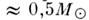 ,
т. е.
,
т. е.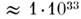 г. Разли-
г. Разли-
чие в массах звёзд оказывается много меньшим,
чем их различие в светимостях (последнее может достигать десятков млн.). Сильно
отличаются радиусы звёзд. В результате диапазон их ср. плотностей от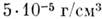 (красные гиганты) до
(красные гиганты) до  (белые
карлики) и даже
(белые
карлики) и даже
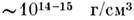 (нейтронные звёзды). Cp. плотность Солнца равна
(нейтронные звёзды). Cp. плотность Солнца равна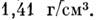
Массу рассеянного звёздного скопления можно
найти, сложив массы всех его членов, светимости к-рых определяют по их видимому
блеску и расстоянию до скопления, а массы - по зависимости масса-светимость.
Массу шарового звёздного скопления Мск далеко не всегда можно оценить путём подсчёта звёзд, т. к. изображения звёзд
центр, области большинства шаровых скоплений на фотографиях, полученных с оптим.
экспозицией, сливаются в одно светящееся пятно. Есть методы оценки общей массы
всего скопления, основанные на статистич. принципах. Так, напр., применение
вириала теоремы позволяет оценить Мск по эфф. радиусу
скопления Rcк и ср. квадрату отклонения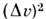 лучевой скорости отд. звёзд от её ср. значения (т. е. от лучевой скорости скопления
как целого):
лучевой скорости отд. звёзд от её ср. значения (т. е. от лучевой скорости скопления
как целого):
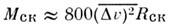
(здесь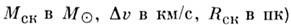
Если возможен подсчёт всех звёзд - членов шарового
скопления, то общую массу скопления можно определить как сумму произведений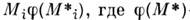 -
функция светимости этого скопления, т. е. функция, показывающая число звёзд, приходящихся
на разл. интервалы значений абс. звёздных величин
-
функция светимости этого скопления, т. е. функция, показывающая число звёзд, приходящихся
на разл. интервалы значений абс. звёздных величин 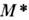 (обычно их подсчитывают в интервалах, равных
(обычно их подсчитывают в интервалах, равных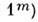 ,
а
,
а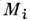 - масса, соответствующая
данной звёздной величине
- масса, соответствующая
данной звёздной величине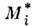 по зависимости масса - светимость. T. о., общая масса скопления
по зависимости масса - светимость. T. о., общая масса скопления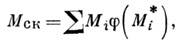
где сумма взята от самых ярких до самых слабых
членов скопления.
Метод определения массы Галактики Мг
использует факт вращения Галактики. Устойчивость вращения позволяет предположить,
в частности, что центро-стремит. ускорение Солнца определяется притяжением массы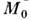 всего вещества Галактики внутри сферы с радиусом
всего вещества Галактики внутри сферы с радиусом 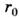 ,
где
,
где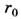 - расстояние
Солнца от центра Галактики, равное прибл.
- расстояние
Солнца от центра Галактики, равное прибл. 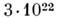 см.
Cp. гравитац. ускорение Солнца
см.
Cp. гравитац. ускорение Солнца 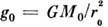 равно
его центростре-мит. ускорению
равно
его центростре-мит. ускорению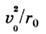 (без
учёта влияния внеш. части Галактики и при условии эллипсоидальности поверхностей
равной плотности в её внутр. части). Собств. галактич. скорость Солнца (т. н.
круговая скорость на расстоянии r0 от центра) v0~
220 км/с, отсюда
(без
учёта влияния внеш. части Галактики и при условии эллипсоидальности поверхностей
равной плотности в её внутр. части). Собств. галактич. скорость Солнца (т. н.
круговая скорость на расстоянии r0 от центра) v0~
220 км/с, отсюда
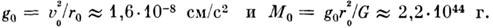
Масса Галактики в сферич. объёме радиусом ~15
кпк, как показывают подобные расчёты, равна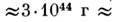
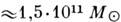 . При этом учитывается также масса всей диффузной (рассеянной) материи в Галактике.
. При этом учитывается также масса всей диффузной (рассеянной) материи в Галактике.
Масса спиральной галактики может быть определена
по результатам изучения её кривой вращения (см. Вращение галактик ).Кривые
вращения указывают на наличие больших масс невидимого (несветящегося) вещества
(т. н. скрытой массы). Масса невидимого вещества галактик может в 10
раз и более превосходить массу светящегося (излучающего) вещества.
Для медленно вращающихся галактик, какими являются,
напр., эллиптич. галактики, трудно получить кривую вращения, но зато можно по
расширению спектральных линий оценить дисперсию скоростей звёзд в системе и,
сопоставив её с истинными размерами галактики, по теореме о вириале оценить
массу эллиптич. галактики.
Ещё один способ оценки масс галактик, входящих
в двойные системы, аналогичен методу оценки масс компонентов спектрально-двойных
звёзд. Используют также установленную статистич. зависимость между массой и
интегральной светимостью галактик разл. типа (своего рода зависимость масса
- светимость для галактик). Светимость определяется по видимой
интегральной звёздной величине галактики и расстоянию
до неё, оценённому по величине красного смещения спектральных линий.
Известные ныне массы галактик заключены в пределах
от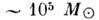 - для т.
н. карликовых галактик до
- для т.
н. карликовых галактик до 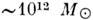 - для сверхгигантских эллиптич. галактик (напр., для галактики М87).
- для сверхгигантских эллиптич. галактик (напр., для галактики М87).
Общая масса галактик, входящих в скопления
галактик, определяется суммированием масс галактик данного скопления с учётом
их типов. С др. стороны, полная масса скопления может быть определена по теореме
о вириале (по дисперсии лучевых скоростей галактик в скоплении в предположении,
что галактики скопления являются гравитационно связанными между собой). Подобные
определения показывают, что полная масса скопления (её наз. вириальной массой)
больше суммы масс отд. галактик скопления. Это свидетельствует о том, что в
межгалактич. пространстве в скоплениях содержится много невидимой (скрытой)
массы. Сверхскопление галактик с центром в созвездии Девы обладает суммарной
массой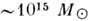
Точность определения M. н. т. зависит от точности
определения всех величин, входящих в соответствующие Формулы. Масса Земли найдена
с погрешностью
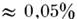 , масса Луны - с погрешностью
, масса Луны - с погрешностью Погрешность определения массы Солнца также составляет
Погрешность определения массы Солнца также составляет 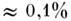 ,
она зависит от точности определения астр, единицы. Вообще, в значит, степени
точность определения массы зависит от точности определения расстояний шкалы, а также расстояний между звёздами (в случае двойных звёзд), линейных размеров
тел и т. д. Массы планет известны с погрешностью от 0,05 до
,
она зависит от точности определения астр, единицы. Вообще, в значит, степени
точность определения массы зависит от точности определения расстояний шкалы, а также расстояний между звёздами (в случае двойных звёзд), линейных размеров
тел и т. д. Массы планет известны с погрешностью от 0,05 до 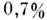 .
Массы звёзд определены с погрешностью
.
Массы звёзд определены с погрешностью 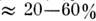 . Неуверенность определения массы галактик можно характеризовать коэф. 2, даже
если надёжно определено расстояние до них.
. Неуверенность определения массы галактик можно характеризовать коэф. 2, даже
если надёжно определено расстояние до них.

Я. Г. Куликовский
|
|