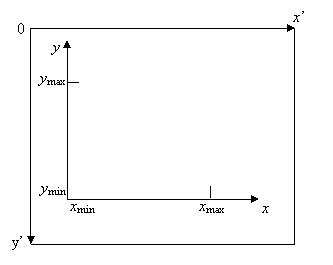
Рис. 1. Экранная и «естественная» системы координат
Теперь для
изображения графика или траектории достаточно ставить точки с помощью процедуры
PutPixel. Если же
требуется изобразить движение тела, то перед выводом на экран очередной точки
достаточно стереть предыдущую.
Изолинии. В задачах моделирования
достаточно стандартная проблема — построение линий (поверхностей), вдоль
которых некоторая функция имеет одинаковое значение, называемых изолиниями
(изоповерхностями). Это очень распространенная задача визуализации
характеристик некоторого скалярного поля в приближении сплошной среды: изотермы
— линии равной температуры, изобары — линии равного давления, изолинии функции
тока жидкости или газа, по которым легко можно представить себе их потоки,
изолинии численностей экологической популяции на местности, изолинии
концентрации вредных примесей в окружающей среде и т.д.
Опишем
типичную процедуру построения изолиний на экране компьютера. На старте мы имеем
двумерную таблицу значений некоторой величины А, полученную в ходе
математического моделирования; числа в этой таблице соответствуют значениям
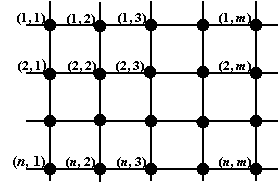
этой величины в узлах пространственной сетки (рис. 2).
Зададим некоторый,
совершенно условный, пространственный шаг h между соседними узлами
по горизонтали и вспомогательную систему координат, в которой узел (1, 1) имеет
координату (0, 0), узел (1, 2) — координату (h, 0), узел
(1, 3) — координату (2h, 0) и т.д. Если шаг по вертикали h*, то узел (i, j) в этой
системе имеет координату
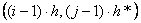 .
.
Предварительно найдем в таблице
наибольшее и наименьшее значения величин aij — допустим, это amin и amax. Пусть b — некоторое промежуточное значение: amin < b < amax.
Обсудим в общих чертах, как построить изолинию А = b. Будем
для этого (в цикле) просматривать вначале все пары ближайших чисел в первой
строке таблицы в поисках такой пары, для которой b находится «внутри». Допустим, число b находится между а1k и a1,k+1, т.е. либо a1k<b< a1,k+1,
либо a1k>b> a1,k+1.
|
a11
|
a12
|
a13
|
…
|
a1m
|
|
a21
|
a22
|
a23
|
…
|
a2m
|
|
¼
|
¼
|
¼
|
¼
|
¼
|
|
an1
|
an2
|
an3
|
…
|
anm
|
Рис. 2. Пространственная сетка и соответствующая ей
таблица значений величины А
С помощью линейной интерполяции
найдем соответствующую горизонтальную координату точки, в которой А = b:


(координата y
определяется номером горизонтальной линии; в данном случае y = 0).
Найденные
координаты запомним и просмотрим первую строку в таблице до конца, затем
просмотрим вторую строку и т.д. Покончив с просмотром строк, мы получим часть
точек, соответствующих изолинии A = b.
После этого
займемся просмотром столбцов. Допустим, во втором столбце нашлась пара чисел,
для которой число b находится между
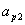 и
и
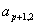 . Она дает следующую точку для изолинии. Закончив просмотр
всех столбцов, мы получим максимально возможный набор координат точек,
принадлежащих данной изолинии. Выведя их на экран в нужном масштабе, получим
точечное изображение изолинии A = b, после
чего можем, взяв другое значение b, построить следующую
изолинию. Более детально эта процедура будет изложена ниже на примере
построения линий равного потенциала электрического поля.
. Она дает следующую точку для изолинии. Закончив просмотр
всех столбцов, мы получим максимально возможный набор координат точек,
принадлежащих данной изолинии. Выведя их на экран в нужном масштабе, получим
точечное изображение изолинии A = b, после
чего можем, взяв другое значение b, построить следующую
изолинию. Более детально эта процедура будет изложена ниже на примере
построения линий равного потенциала электрического поля.
Условные цвета, условное контрастирование
Еще один интересный прием современной научной графики — условная раскраска. Она
находит широчайшее применение в самых разных приложениях науки и представляет
собой набор приемов по максимально удобной, хотя и очень условной, визуализации
результатов компьютерного моделирования.
Приведем примеры.
В различных исследованиях температурных полей встает проблема наглядного
представления результатов. Самый простой (и самый неудобный для восприятия) способ
— привести карту, в некоторых точках которой обозначены значения температур.
Другой способ,
описанный выше (набор изотерм) — гораздо нагляднее. Но можно добиться еще
большей наглядности, учитывая, что большинству людей свойственно, сравнивая
разные цвета, воспринимать красный как «горячий», голубой как «холодный», а все
остальные — между ними. Допустим, что на некоторой территории температура в
данный момент имеет в разных местах значения от –25°С до + 15°С. Разделим этот
диапазон на участки с шагом, равным, например, 5°
[–25,
–20], [–20, –15], …, [+ 10, +15],
и закрасим
первый из них в ярко-голубой, последний — в ярко-красный, а все остальные — в
промежуточные оттенки голубого и красного цветов. Получится замечательная
наглядная картина температурного поля.
А что делать,
если дисплей монохромный? Или если изображение надо перенести с цветного
дисплея на бумагу при отсутствии возможности цветной печати? Тогда роль цвета
может сыграть контраст. Сделаем самый «горячий» участок самым темным, самый
«холодный» — прозрачным, а остальные — промежуточными.
Есть достаточно
много моделей, в которых естественно прибегнуть к подобному приему
визуализации. В частности, в задаче о теплопроводности в стержне, при
моделировании распределения электрических полей. Если заниматься имитационным
моделированием конкурирующих популяций, то, раскрасив их в разные цвета, можно
получить на экране причудливые картины, передающие ход конкурентной борьбы.
Условные раскраски
бывают и гораздо более абстрактными, чем в описанных выше случаях. При
моделировании сложных органических молекул компьютер может выдавать результаты
в виде многоцветной картины, на которой атомы водорода изображены одним цветом,
углерода — другим и т.д., причем атом представлен шариком (кружочком), в
пределах которого плотность цвета меняется в соответствии с распределением
электронной плотности.
При поиске
полезных ископаемых методами аэрофотосъемки с самолетов или космических
спутников компьютеры строят условные цветовые изображения распределений
плотности ископаемых под поверхностью Земли.
Подведем
итог: изображения в условных цветах и контрастах — мощнейший прием научной
графики. Он позволяет понять строение не только плоских, но и объемных
(трехмерных) объектов, дает в руки исследователя один из замечательных методов
познания. Приведем в качестве иллюстрации пример программы условной раскраски
неравномерно нагретого стержня в разные моменты времени (по заранее
заготовленным данным).
Program Stergen;
Uses Crt_ii, Graph;
Type Mas2 = array[0..10,0..4] of Real;
Const {Массив распределения температуры в разные моменты времени}U : Mas2 =
((3.000, 3.667, 4.333, 5.000, 3.000), (3.000, 3.628, 4.128, 3.952, 3.000),
(3.000, 3.514, 3.783, 3.593, 3.000), (3.000, 3.377, 3.546, 3.396, 3.000),
(3.000, 3.267, 3.381, 3.272, 3.000), (3.000, 3.187, 3.266, 3.188, 3.000),
(3.000, 3.131, 3.185, 3.131, 3.000), (3.000, 3.091, 3.129, 3.091, 3.000),
(3.000, 3.064, 3.090, 3.064, 3.000), (3.000, 3.044, 3.063, 3.044, 3.000),
(3.000, 3.031, 3.044, 3.031, 3.000));
Var
M,I,J,Nl,Nt: Integer; MaxF,L,T,Hl,Ht: Real;
Procedure Initialize; {Процедура инициализации графического режима}Var GraphDriver, GraphMode : Integer;
Begin
GraphDriver:=Detect;
InitGraph(GraphDriver, GraphMode,'c:\bp\bgi');
End;
{Графическая иллюстрация решения}Procedure Postanovka (U : Mas2; Nt, Nl : Integer; Hl, L, MaxF : Real);
Var X_N, Shag, Y_N, Shir, Dlin, Color, I, J, K, Y : Integer;
Flag : Boolean; Ff : String; Col : Array [0..15] Of Byte;
Begin
Initialize; {Инициализация графического режима} X_N:= GetMaxX Div 6;
If Nt <= 6 Then M:= Nt Else M:= Nt Div 2;
Y_N:= GetMaxY Div M-20; Shir:= Y_N Div 2;
Dlin:= GetMaxX-2*(X_N); Shag:= Trunc(Dlin / Nl); Str(Shag, Ff);
Col[0]:= 0; Col[1]:= 8; Col[2]:= 1; {Палитра цветов}
Col[3]:= 9; Col[4]:= 3; Col[5]:= 11;
Col[6]:= 2; Col[7]:= 10; Col[8]:= 14;
Col[9]:= 13; Col[10]:= 5; Col[11]:= 12; Col[12]:= 4;
For I:= 0 To M-1 Do {Номер временного промежутка} Begin
For J := 0 To Nl-1 Do {Номер участка стержня} Begin
Flag := False;
For K := 0 To Shag Do
Begin
For y := 0 To Shir Do
Begin
Color :=1 + Round((U[I, J] + {определение номера цвета} (U[I,J + 1] - U[I,J]) * K/Shag-U[0,0])/3*16);
If Random(64) > 32
Then If Random(64) > 32 Then Color:= Color + 1 Else
Color := Color - 1;
If Not Flag Then {вывод текущей температуры} Begin
Str((U[I, J] + (U[I, J]) * K / Shag) : 5 : 3, Ff);
OutTextXY(K+X_N+Shag * J, Y_N * (1+I) - 19, Ff);
Flag := True
End;
{рисование точки} PutPixel(K+X_N+Shag * J, Y + Y_N * (1+I), Col[Color]);
End;
End
End
End;
SetColor(White);
SetTextStyle(1,0,2);
OutTextXY(150, 420, 'нажмите любую клавишу');
Repeat Until Keypressed;
CloseGraph;
End;
Begin {OCHOBHAЯ ПРОГРАММА} L:= 4; T:= 10; Hl:= 1; Ht := 1;
Nl := Trunc(L / Hl); Nt := Trunc(T / Ht); MaxF := 5;
Postanovka (U, Nt, Nl, Hl, L, MaxF)
End.
Знаете ли Вы, что объективно обусловленная оценка ресурса (продукции) - это величина прироста экономического эффекта, обусловленного малым изменением доступного объёма ресурса или величины планового задания по выпуску продукции. При использовании экономико-математического моделирования численно равна двойственной оценке соответствующего ограничения. Измеряется в единицах измерения экономического эффекта в расчёте на единицу ресурса (продукции).
НОВОСТИ ФОРУМА

Рыцари теории эфира | | 10.11.2021 - 12:37: ПЕРСОНАЛИИ - Personalias -> WHO IS WHO - КТО ЕСТЬ КТО - Карим_Хайдаров.
10.11.2021 - 12:36: СОВЕСТЬ - Conscience -> РАСЧЕЛОВЕЧИВАНИЕ ЧЕЛОВЕКА. КОМУ ЭТО НАДО? - Карим_Хайдаров.
10.11.2021 - 12:36: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от д.м.н. Александра Алексеевича Редько - Карим_Хайдаров.
10.11.2021 - 12:35: ЭКОЛОГИЯ - Ecology -> Биологическая безопасность населения - Карим_Хайдаров.
10.11.2021 - 12:34: ВОЙНА, ПОЛИТИКА И НАУКА - War, Politics and Science -> Проблема государственного терроризма - Карим_Хайдаров.
10.11.2021 - 12:34: ВОЙНА, ПОЛИТИКА И НАУКА - War, Politics and Science -> ПРАВОСУДИЯ.НЕТ - Карим_Хайдаров.
10.11.2021 - 12:34: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от Вадима Глогера, США - Карим_Хайдаров.
10.11.2021 - 09:18: НОВЫЕ ТЕХНОЛОГИИ - New Technologies -> Волновая генетика Петра Гаряева, 5G-контроль и управление - Карим_Хайдаров.
10.11.2021 - 09:18: ЭКОЛОГИЯ - Ecology -> ЭКОЛОГИЯ ДЛЯ ВСЕХ - Карим_Хайдаров.
10.11.2021 - 09:16: ЭКОЛОГИЯ - Ecology -> ПРОБЛЕМЫ МЕДИЦИНЫ - Карим_Хайдаров.
10.11.2021 - 09:15: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от Екатерины Коваленко - Карим_Хайдаров.
10.11.2021 - 09:13: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от Вильгельма Варкентина - Карим_Хайдаров.
|
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


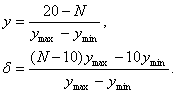
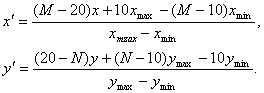
![]()
![]()
![]()
![]()
![]()
![]()