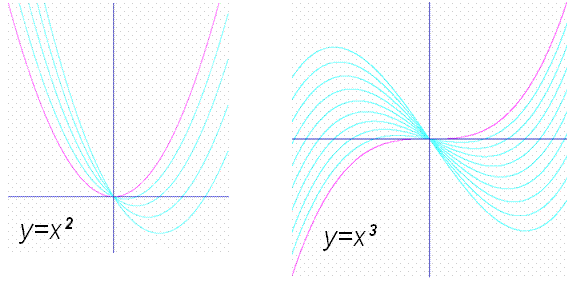
Снежная лавина, разрыв надуваемого шарика, молния – примеры процессов у которых есть общее – они происходят в результате постепенного изменения параметров, завершающееся процессом, проходящим очень быстро и качественно изменяющим систему. В самом деле, на склоне горы постепенно накапливается снег. Он неподвижен. И вдруг, в одно мгновение, многотонная снежная масса срывается с места и стремительно спускается вниз. Другой пример. Вы надуваете резиновый шарик, его размер плавно увеличивается. И вдруг шарик лопается. Молния также ударяет внезапно, когда напряженность электрического поля между облаком и землей достигает критического значения. Можно привести еще десятки сходных примеров. Катастрофами называют скачкообразные изменения, возникающие в виде внезапного ответа системы на плавное изменение внешних условий. В настоящее время разработана и быстро развивается математическая теория, изучающая подобные процессы. Ее называют математической теорией катастроф (не путать с эволюционной теорией кастастроф Кювье).
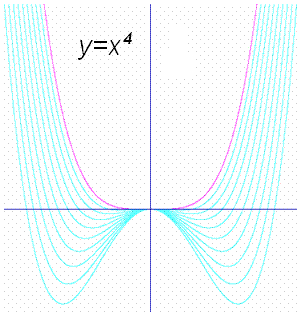
Один из аспектов задач на экстремум, который долгое время оставался вне поля зрения математиков, тесно связан с современным понятием структурной устойчивости функций. Если мы рассмотрим, например, функции y = x2, y = x3 и y = x4, то все они имеют нулевую первую производную в начале координат (в таких случаях говорят, что х = 0 - критическая точка). Первая и третья функции имеют в критической точке минимальное значение, а вторая - точку перегиба, и в традиционных рамках задач на экстремум это различие представляется наиболее важным. Но выберем несколько иную точку зрения. Попробуем слегка «пошевелить» рассматриваемые функции, введя слабые возмущения: 1) y = x2 - eх; 2) y = x3 - eх; 3) y = x4 - eх2, где параметр e может быть сколь угодно малым по величине. В результате такого возмущения в случае (1) никаких принципиальных изменений не происходит: сохраняется единственная критическая точка, которая лишь смещена на малую величину x0 = e/2, причем значение функции в этой точке (единственный минимум) изменяется на величину у0 = - e2/4. Во втором и третьем случаях ситуация совсем иная. Вторая функция, для которой начало координат было точкой перегиба, приобретает две экстремальные точки одна из которых соответствует минимуму, а другая - максимуму. Функция y = x4, имевшая единственный минимум в начале координат, в результате малого шевеления имеет уже три критические точки. При этом начало координат становится точкой максимума, а в двух новых критических точках, сколь угодно близких к точке х = 0, функция принимает минимальные значения.
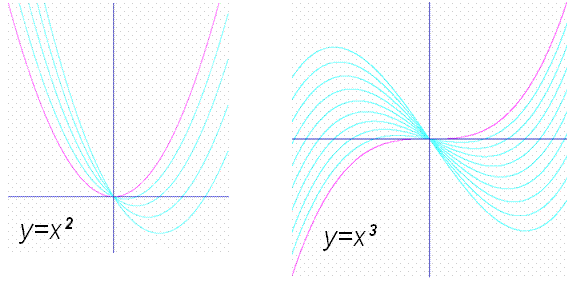
Построение математической модели любого физического процесса связано с пренебрежением малыми членами. В нашем первом примере это вполне оправданно: учет малого отклонения функции от квадратной параболы приводит не к качественным, а к малым количественным изменениям. Во втором и третьем примерах поведение при учете малых поправочных членов качественно иное. Таким образом, функции y = x3 и y = x4, несмотря на то что вторая из них имеет экстремум, а первая нет, объединяет общее свойство, которое, не прибегая к строгим определениям, назовем структурной неустойчивостью. Этот термин отражает то, что при малом изменении структуры функции ее поведение в окрестности критической точки резко изменяется. Наоборот, функция y = x2 структурно устойчива.
Свойство структурной устойчивости (неустойчивости) функции не было включено в арсенал математических понятий вплоть до 30-х годов XX века, когда оно впервые было сформулировано А.А. Андроновым (1901-1952). Через несколько десятилетий понятие о структурной устойчивости стало одним из ключевых для теории катастроф.
Казалось бы, в связи со сказанным структурно неустойчивые в критических точках функции непригодны для описания реальности. Но, как правило, функции, возникающие в физических приложениях, содержат некоторые параметры, значения которых могут изменяться в определенном диапазоне (подобно параметру e в наших примерах). В таких случаях мы имеем дело с семейством функций, зависящим от параметра. Может случиться, что при изменении последнего с неизбежностью достигается значение (в нашем примере e = 0), соответствующее структурно неустойчивой критической точке, которая тем самым приобретает вполне реальный смысл. Более того, именно эта точка, будучи одной из реализаций семейства критических точек, является наиболее важной, поскольку с ней связаны качественные изменения в поведении системы (подобные описанным выше).
Анализ семейств функций в связи с задачами на минимум и максимум также не стал предметом общематематических построений ни в XVIII, ни в первой половине XIX века. Только великий французский математик А. Пуанкаре увидел в таком анализе общематематическую проблему. В связи с его формулировкой этой проблемы возникло понятие "бифуркация", также ставшее позднее одним из ключевых в теории катастроф. Термин "бифуркация" буквально означает "раздвоение", но обычно применяется в более широком смысле для обозначения всевозможных качественных перестроек различных объектов при изменении параметров, от которых они зависят. В примере с семейством y = x4 - eх2 значение параметра e = 0 соответствует также точке бифуркации, поскольку при переходе e от отрицательных значений к положительным единственное устойчивое стационарное состояние х = 0, становясь неустойчивым, дополняется парой устойчивых состояний В примере же с семейством функций y = x3 ‑ eх при отрицательных e стационарные состояния вообще отсутствуют, а в точке e = 0 происходит рождение пары таких состояний, одно из которых устойчиво, а второе неустойчиво. В обоих случаях значения e = 0 соответствуют точкам бифуркации, хотя и различных типов.
Теория катастроф определяет область существования различных структур, границы их устойчивости. Для изучения же динамики систем необходимо знать каким именно образом новые решения уравнений «ответвляются» от известного решения. Ответ на такие вопросы дает теория бифуркаций (разветвлений), то есть возникновения нового решения при критическом значении параметра. Момент перехода (катастрофический скачок) зависит от свойств системы и уровня флуктуаций.
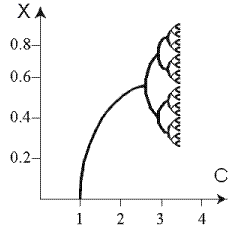
В реальных условиях при углублении неравновесности в открытой системе возникает определенная последовательность бифуркаций, сопровождающаяся сменой структур. Типичным примером такого сценария является развитие турбулентности с чередующимися типами все более усложняющихся движений. Состояние системы в момент бифуркации является неустойчивым и бесконечно малое воздействие может привести к выбору дальнейшего пути. Финальным состоянием эволюционирующих физических систем является состояние динамического хаоса. Иллюстрацией перехода к нему является логистическое уравнение:
Xn+1=CXn(I - Xn)
Для наглядности рассмотрим биологическую трактовку этого уравнения: изолированно живет популяция особей нормированной численностью Xn. Через год появляется потомство численностью Xn+1. Рост популяции описывается первым членом правой части уравнения - СХn где коэффициент С определяет скорость роста и является определяющим параметром. Убыль (за счет перенаселенности, недостатка пищи и т.п.) определяется вторым, нелинейным членом - (СХn)2. Зависимость численности популяции от параметра С приведена на рисунке. Линии показывают значения Xn при больших n (n->oo). При С < 1 популяция с ростом n вымирает. В области 1 < С < 3 численность популяции приближается к постоянному значению Х0 = 1 - 1/c. Это область стационарных решений. Затем в диапазоне 3 < С < 3,57 появляются бифуркации, разветвление кривых на две. Численность популяции колеблется между двумя значениями, лежащими на этих ветвях. Сначала популяция резко возрастает, на следующий год возникает перенаселенность и через год численность снова становится малой. Далее происходит перекрывание областей различных решений и поведение системы становится хаотическим. Динамические переменные Xn принимают значения сильно эависящие от начальных. При расчетах на ЭВМ для близких начальных значений С решения могут резко отличаться. Более того, расчеты становятся некорректными, так как начинают зависеть от случайных процессов в самой ЭВМ. М.Фейгенбаум установил универсальные закономерности перехода к динамическому хаосу при удвоении периода, которые были экспериментально подтверждены для широкого класса механических, гидродинамических, химических и т.д. систем. Наряду с последовательностями удвоений периода (каскадами Фейгенбаума) имеются другие пути перехода к хаосу, когда, например, длительные периоды упорядоченного движения чередуются со вспышками беспорядка.
Ниже приведена программа на языке Visual Basic, в которой строятся каскады Фейгенбаума, ее код:
|
Результаты работы программы при разных значения n = 5, 7, 9, 11, 100:
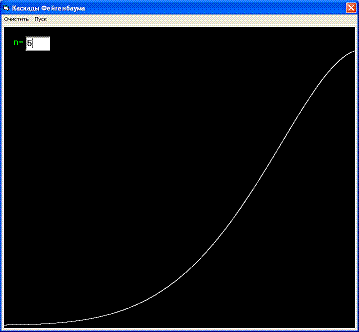
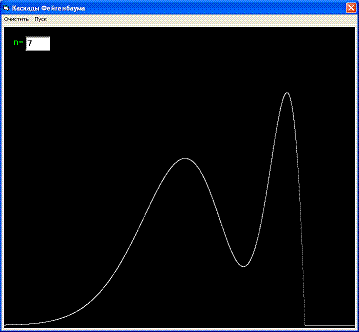
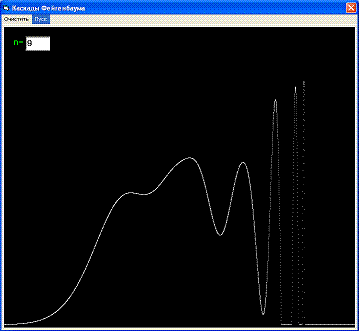
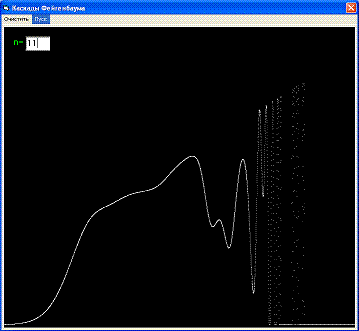
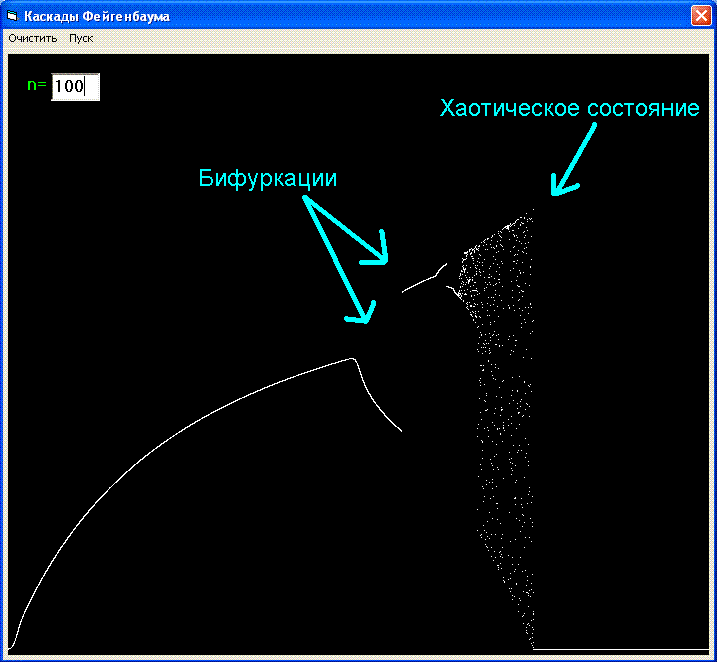
На последнем изображении ясно видны бифуркации и переход процесса в хаотическое состояние.