Кому не случалось стоять в очереди и с нетерпением прикидывать, успеет ли он сделать покупку (или заплатить за квартиру, покататься на карусели и т.д.) за некоторое имеющееся в его распоряжении время? Или, пытаясь позвонить по телефону в справочную и натыкаясь несколько раз на короткие гудки, нервничать и оценивать - дозвонюсь или нет? Из таких "простых" проблем в начале XX века родилась весьма непростая наука - теория массового обслуживания, использующая аппарат теории вероятностей и математической статистики, дифференциальных уравнений и численных методов. Основоположником ее стал датский ученый А. К. Эрланг, исследовавший проблемы функционирования телефонных станций.
Впоследствии выяснилось, что новая наука имеет многочисленные выходы в экономику, военное дело, организацию производства, биологию и экологию; по ней написаны десятки книг, тысячи журнальных статей.
Компьютерное моделирование при решении задач массового обслуживания, реализуемое в виде метода статистических испытаний (метода Монте-Карло), хоть и не является в теории массового обслуживания основным, но играет в ней важную роль. Основная линия в ней - получение результатов аналитических, т.е. представленных формулами. Однако, возможности аналитических методов весьма ограничены, в то время как метод статистических испытаний универсален и весьма прост для понимания (по крайней мере кажется таковым).
Рассмотрим одну из простейших задач данного класса. Имеется магазин с одним продавцом, в который случайным образом входят покупатели. Если продавец свободен, он начинает обслуживать покупателя сразу, если покупателей несколько, выстраивается очередь.
Вот аналогичные задачи:
Будем для определенности говорить о магазине, покупателях и продавце. Рассмотрим возникающие здесь проблемы, которые заслуживают математического исследования и, как выясняется, весьма серьезного.
Итак, на входе этой задачи случайный процесс прихода покупателей в магазин. Он является "марковским", т.е. промежутки между приходами любой последовательной пары покупателей - независимые случайные события, распределенные по некоторому закону. Реальный характер этого закона может быть установлен лишь путем многочисленных наблюдений; в качестве простейшей модельной функции плотности вероятности можно взять равновероятное распределение в диапазоне времени от 0 до некоторого T - максимально возможного промежутка между приходами двух последовательных покупателей. При этом распределении вероятность того, что между приходами двух покупателей пройдет 1 минута, 3 минуты или 8 минут одинакова (если T > 8).
Такое распределение, конечно, малореалистично; реально оно имеет при некотором значении t = τ максимум и быстро спадает при больших t, т.е. имеет вид, изображенный на рис. 1.
Можно, конечно, подобрать немало элементарных функций, графики которых похожи на тот, что изображен на рис. 1. Например, семейство функций Пуассона, широко используемых в теории массового обслуживания:
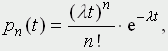 |
(1) |
где λ - некоторая константа, n - произвольное целое.
| Функции (1) имеют максимум при | и нормированы: |
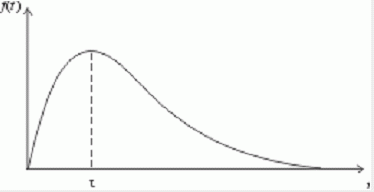
Рис. 1. Типичная плотность вероятности распределения времени между приходами покупателей
Второй случайный процесс в этой задаче, никак не связанный с первым, сводится к последовательности случайных событий - длительностей обслуживания каждого из покупателей. Распределение вероятностей длительности обслуживания качественно имеет тот же вид, что и в предыдущем случае; при отработке первичных навыков моделирования методом статистических испытаний вполне уместно принять модель равновероятного распределения.
В таблице 1 в колонке A записаны случайные числа - промежутки между приходами покупателей (в минутах), в колонке B - случайные числа - длительности обслуживания (в минутах). Для определенности взято amax = 10 и bmax = 5. Из этой короткой таблицы, разумеется, невозможно установить, каковы законы распределения приняты для величин A и B; в данном обсуждении это не играет никакой роли. Остальные колонки предусмотрены для удобства анализа; входящие в них числа находятся путем элементарного расчета. В колонке C представлено условное время прихода покупателя, в колонке D - момент начала обслуживания, E - момент конца обслуживания, F - длительность времени, проведенного покупателем в магазине в целом, G - в очереди в ожидании обслуживания, H - время, проведенное продавцом в ожидании покупателя (магазин пуст). Таблицу удобно заполнять по горизонтали, переходя от строчки к строчке. Приведем для удобства соответствующие формулы (в них i = 1, 2, 3, ...):
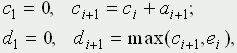
- так как начало обслуживания очередного покупателя определяется либо временем его прихода, если магазин пуст, либо временем ухода предыдущего покупателя;

| N | A | B | C | D | E | F | G | H |
| 1 | 0 | 4 | 0 | 0 | 4 | 4 | 0 | 0 |
| 2 | 2 | 1 | 2 | 4 | 5 | 3 | 2 | 0 |
| 3 | 10 | 5 | 12 | 12 | 17 | 5 | 0 | 7 |
| 4 | 1 | 2 | 13 | 17 | 19 | 6 | 4 | 0 |
| 5 | 6 | 3 | 19 | 19 | 22 | 3 | 0 | 0 |
Табл 1. Моделирование очереди
Таким образом, при данных случайных наборах чисел в колонках A и B и покупателям приходилось стоять в очереди (колонка G), и продавцу - в ожидании покупателя (колонка H).
При моделировании систем такого вида возникают следующие вопросы. Какое среднее время приходится стоять в очереди к прилавку? Чтобы ответить на него, следует найти
в некоторой серии испытаний. Аналогично можно найти среднее значение величины h. Конечно, эти выборочные средние сами по себе - случайные величины; в другой выборке того же объема они будут иметь другие значения (при больших объемах выборки, не слишком отличающиеся друг от друга). Доверительные интервалы, в которых находятся точные средние значения (т.е. математические ожидания соответствующих случайных величин) при заданных доверительных вероятностях находятся методами математической статистики.
Сложнее ответить на вопрос, каково распределение случайных величин G и H при заданных распределениях случайных величин A и B. Допустим, в простейшем моделировании мы примем гипотезу о равновероятных распределениях величин A и B - скажем, для A в диапазоне от 0 до 10 минут и B - от 0 до 5 минут. Для построения методом статистических испытаний распределений величин G и H поступим так: найдем в достаточно длинной серии испытаний (реально - в десятках тысяч, что на компьютере делается достаточно быстро) значения gmax (для H все делается аналогично) и разделим промежуток [0, gmax] на m равных частей - скажем, вначале на 10 - так, чтобы в каждую часть попало много значений gi. Разделив число попаданий nk в каждую из частей на общее число испытаний n, получим набор чисел
Построенные по ним гистограммы дают представление о функциях плотностей вероятности соответствующих распределений. По гистограмме можно составить представление о функции плотности распределения соответствующей случайной величины. Для проверки же гипотезы о принадлежности такого эмпирически найденного распределения тому или иному конкретному виду служат известные статистические критерии.
Располагая функцией распределения (пусть даже эмпирической, но достаточно надежной), можно ответить на любой вопрос о характере процесса ожидания в очереди. Например: какова вероятность прождать дольше m минут? Ответ будет получен, если найти отношение площади криволинейной трапеции, ограниченной графиком плотности распределения, прямой x = m и y = 0, к площади всей фигуры.
Программа моделирование очереди позволяет моделировать описанный выше процесс. На выходе она дает средние значения и дисперсии случайных величин g и h, полученные по выборке, максимальный объем которой порядка 10000 (ограничение связано с малой допустимой длиной массива в PASCALе; чтобы его смягчить, использовано динамическое описание массивов g и h). Кроме того, программа строит гистограммы распределений величин g и h.
|
|