Часто в системах самого различного назначения протекают процессы, которые можно представить в виде модели "гибели и размножения".
Граф состояний такого процесса показан на рис. 2.5.
Особенностью модели является наличие прямой и обратной связей с каждым соседним состоянием для всех средних состояний; первое и последнее (крайние) состояния связаны только с одним "соседом" (с последующим и предыдущим состояниями соответственно).
Название модели - "гибель и размножение" - связано с представлением, что стрелки вправо означают переход к состояниям, связанным с ростом номера состояния ("рождение"), а стрелки влево - с убыванием номера состояний ("гибель").
Очевидно, стационарное состояние в этом процессе существует. Составлять уравнения Колмогорова нет необходимости, так как структура регулярна, необходимые формулы приводятся в справочниках, а также в рекомендованной литературе.
Для приведенных на рис. 2.5 обозначений формулы имеют вид:
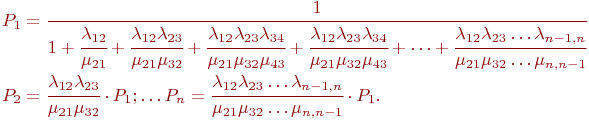
Пример 2.3. Имеется система из двух одинаковых и работающих параллельно компьютеров.
Требуется определить надежностные характеристики этой системы.
Решение
В этой системе возможны три состояния:
- оба компьютера исправны;
- один компьютер исправен, другой ремонтируется;
- оба компьютера неисправны и ремонтируются. Будем
полагать, что процессы отказов и восстановлений - однородные
марковские, одновременный выход из строя обоих компьютеров, как и
одновременное восстановление двух отказавших компьютеров практически
невозможно.
Поскольку компьютеры одинаковые, то с точки зрения
надежности, неважно, какой именно компьютер неисправен в состоянии
важно, что один.
С учетом сказанного, ситуация моделируется схемой "гибели и размножения" (рис. 2.6).
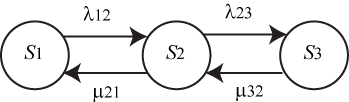
На рис. 2.6:
, 
- интенсивности потоков отказов;
- интенсивности потоков восстановлений.
Пусть среднее время безотказной работы каждого компьютера
. , а среднее время восстановления одного компьютера 
.
Тогда интенсивность отказов
одного компьютера будет равна 
а интенсивность восстановления одного компьютера - 
В состоянии 
работают оба компьютера, следовательно:
В состоянии работает один компьютер, значит:
В состоянии восстанавливается один компьютер, тогда:
В состоянии восстанавливаются оба компьютера:
Используем зависимости (2.2). Вероятность состояния, когда обе машины исправны:
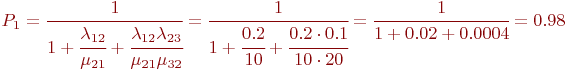
Вероятность второго состояния (работает один компьютер):
Аналогично вычисляется и 
Хотя найти 
можно и так:
Пример 2.4. В полосе объединения работают передатчики противника. Подразделение операторов-связистов армейской контрразведки ведет поиск передатчиков по их радиоизлучениям. Каждый оператор, обнаружив передатчик противника, следит за его частотой, при этом новым поиском не занимается. В процессе слежения частота может быть потеряна, после чего оператор снова осуществляет поиск.
Разработать математическую модель для определения эффективности службы подразделения операторов. Под эффективностью понимается среднее число обнаруженных передатчиков за установленный промежуток времени.
Решение
Будем считать, что наши операторы и радисты противника обладают высокой квалификацией, хорошо натренированы. Следовательно, можно принять, что интенсивности обнаружения частот передатчиков противника и потерь слежения - постоянны. Обнаружение частоты и ее потеря зависят только от того, сколько запеленговано передатчиков в настоящий момент и не зависят от того, когда произошло это пеленгование. Следовательно, процесс обнаружения и потерь слежения за частотами можно считать непрерывным однородным марковским процессом.
Исследуемое свойство этой системы пеленгации: загруженность операторов, что, очевидно, совпадает с числом обнаруженных частот.
Введем обозначения:
- количество операторов;
- количество передатчиков противника, полагаем 
;
- среднее число операторов, ведущих слежение;
- среднее число запеленгованных передатчиков;
- интенсивность пеленгации передатчика противника одним
оператором;
- интенсивность потока потерь слежения оператором;
- текущая численность запеленгованных передатчиков 
В системе пеленгации возможны следующие состояния:
- запеленгованных передатчиков нет, поиск ведут 
операторов, вероятность состояния 
;
- запеленгован 1 передатчик, поиск ведут 
операторов, вероятность состояния 
;
- запеленгованы 2 передатчика, поиск ведут 
операторов, вероятность состояния 
;
…
- запеленгованы 
передатчиков, вероятность 
;
…
- запеленгованы 
передатчиков, вероятность 
Цель моделирования - - достигается вычислением:
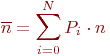
Как и в примере 2.3 полагаем, что одновременное обнаружение или потеря двух и более частот практически невозможно. Граф состояний системы показан на рис. 2.7.
Граф соответствует процессу "гибели и размножения", полносвязный, число состояний системы, конечно, значит, установившийся режим, и предельные значения вероятностей в системе пеленгации существуют.
Пусть, к примеру, количество операторов 
, а количество передатчиков противника 
. В этом случае граф состояний имеет вид (рис. 2.8):
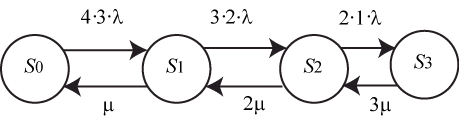
Для упрощения вычислений примем 
. Тогда для этой схемы "гибели и размножения" по
зависимостям (2.2) имеем:
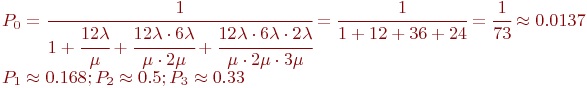
Окончательно:
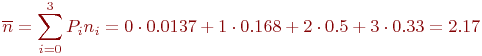
Таким образом, в условиях данного примера в среднем будут пеленговаться не менее двух передатчиков противника.
Непрерывный марковский процесс полностью определяется
значениями плотностей вероятностей
переходов 
, 
Ранее был установлен их физический смысл как интенсивности
потоков событий, переводящих систему из одного состояния в другое.
Поток событий в однородных непрерывных марковских процессах
характеризуется экспоненциальным законом распределения случайных
интервалов времени между событиями. Такой поток называют простейшим или стационарным пуассоновским.
Простейший поток обладает свойствами:
Боев В.Д., Сыпченко Р.П. Компьютерное моделирование
|
|
 |
