моделирование СМО ОКМ ДМ экономическая информатика 4GL Теория и практика обработки информации

Моделирование по схеме непрерывных марковских процессов

Cyщecтвyeт широкий класс систем, которые меняют свои состояния в случайные моменты времени . Как и в предыдущем случае, в этих системах рассматривается процесс с дискретными состояниями . Например, переход объекта от исправного состояния к неисправному, соотношение сил сторон в ходе боя и т. п. Оценка эффективности таких систем определяется с помощью вероятностей каждого состояния на любой момент времени , .

Чтобы определить вероятности состояния системы для любого момента времени необходимо воспользоваться математическими моделями марковских процессов с непрерывным временем (непрерывных марковских процессов).

При моделировании состояния систем с непрерывными марковскими процессами мы уже не можем воспользоваться переходными вероятностями , так как вероятность "перескока" системы из одного состояния в другое точно в момент времени равна нулю (как вероятность любого отдельного значения непрерывной случайной величины).

Поэтому вместо переходных вероятностей вводятся в рассмотрение плотности вероятностей переходов :

где - вероятность того, что система, находившаяся в момент времени в состоянии за время перейдет в состояние .

С точностью до бесконечно малых второго порядка из приведенной формулы можно представить:

Непрерывный марковский процесс называется однородным,если плотности вероятностей переходов не зависят от времени (от момента начала промежутка ). В противном случае непрерывный марковский процесс называется неоднородным.

Целью моделирования,как и в случае дискретных процессов, является определение вероятностей состояний системы Эти вероятности находятся интегрированием системы дифференциальных уравнений Колмогорова.

Сформулируем методику моделирования по схеме непрерывных марковских процессов.

Определить состояния системы и плотности вероятностей переходов .
Составить и разметить граф состояний.
Составить систему дифференциальных уравнений Колмогорова. Число уравнений в системе равно числу состояний. Каждое уравнение формируется следующим образом.
B левой части уравнения записывается производная вероятности -го состоянии
В правой части записывается алгебраическая сумма произведений и . Число произведений столько, сколько стрелок связано с данным состоянием. Если стрелка графа направлена в данное состояние, то соответствующее произведение имеет знак плюс, если из данного состояния - минус.
Определить начальные условия и решить систему дифференциальных уравнений.

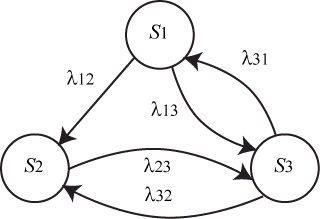
Пример 2.2. Составить систему дифференциальных уравнений Колмогорова для нахождения вероятностей состояний системы, размеченный граф состояний которой представлен на рис. 2.3.

Рис. 2.3. Размеченный граф состояний

Решение

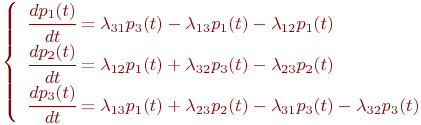
Очевидно, .

Поэтому любое из первых трех уравнений можно исключить, как линейно зависимое.

Для решения уравнений Колмогорова необходимо задать начальные условия. Для рассмотренного примера 2.2, можно задать такие начальные условия: , .

Однородный марковский процесс с непрерывным временем можно трактовать как процесс смены состояний под влиянием некоторого потока событий. То есть плотность вероятности перехода можно трактовать как интенсивность потока событий, переводящих систему из -го состояния в -е. Такими потоками событий являются отказы техники, вызовы на телефонной станции, рождение и т. п.

При исследовании сложных объектов всегда интересует: возможен ли в исследуемой системе установившейся (стационарный) режим? То есть, как ведет себя система при ? Существуют ли предельные значения ? Как правило, именно эти предельные значения интересуют исследователя.

Ответ на данный вопрос дает теорема Маркова.

Если для однородного дискретного марковского процесса с конечным или счетным числом состояний все , то предельные значения существуют и их значения не зависят от выбранного начального состояния системы.

Применительно к непрерывным марковским процессам теорема Маркова трактуется так: если процесс однородный и из каждого состояния возможен переход за конечное время в любое другое состояние и число состояний счетно или конечно, то предельные значения существуют и их значения не зависят от выбранного начального состояния.

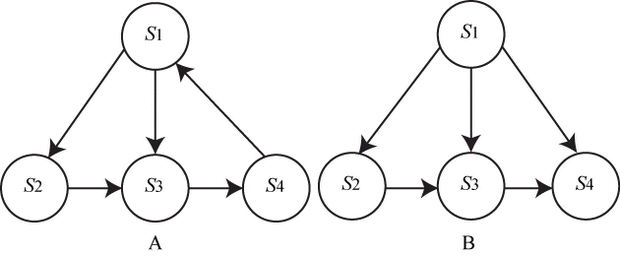
Например (рис. 2.4), в системе А стационарный режим есть, а в системе В стационарного режима нет: если система окажется в состоянии она не сможет перейти ни в какое другое состояние.

Рис. 2.4. Примеры графов состояний систем с различными режимами

Ссылки

Боев В.Д., Сыпченко Р.П. Компьютерное моделирование

моделирование СМО ОКМ ДМ экономическая информатика 4GL Теория и практика обработки информации

Знаете ли Вы, что системный анализ - это метод научного познания, нацеленный на установление структуры исследуемой системы. Метод системного анализа является необходимой предпосылкой метода математического моделирования.

НОВОСТИ ФОРУМА

Рыцари теории эфира