

Имитационное моделирование широко применяется в физике, биологии, социологии, экономике. Рассмотрим одну из самых распространенных имитационных моделей, предложенную Джоном Канвеем - игра "Жизнь"

|
|
|

|
|
|
Для построения алгоритма игры рассмотрим квадратное поле из n+1 столбцов и строк с обычной нумерацией от 0 до n. Крайние граничные столбцы и строки для удобства определим как "мертвую зону", они играют лишь вспомогательную роль.
Для любой внутренней клетки поля с координатами (i,j) можно определить 8 соседей. Примем, что если клетка живая, то ее закрашиваем, если клетка мертвая, то она пустая.
Зададим правила игры.
Если клетка (i,j) живая и в окружении более трех живых клеток, то она погибает (от перенаселения). Живая клетка также погибает, если в окружении менее двух живых клеток (от одиночества). Мертвая клетка оживает, если вокруг нее имеется три живые клетки.
Начальное количество живых клеток и расположение их на поле определяется либо случайным образом, либо мы можем задать нужное нам количество живых клеток и определить их расположение определенным образом и смотреть, как они будут себя вести. Есть устойчивые структуры - пропеллер - три клетки в ряд, есть стабильные структуры - квадрат с просветом внутри, есть структуры, которые повторяют себя через определенное количество циклов и т.д.
Если располагать клетки случайным образом, то с помощью игры жизнь можно построить модель внутривидовой конкуренции (трава - зайцы), межвидовой конкуренции (зайцы - лисы), модель распространения инфекции (эпидемия) и т.д.
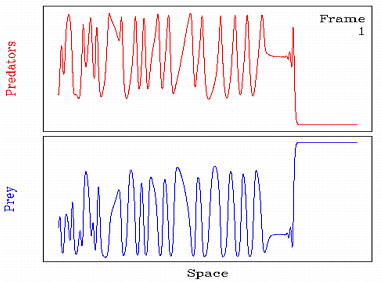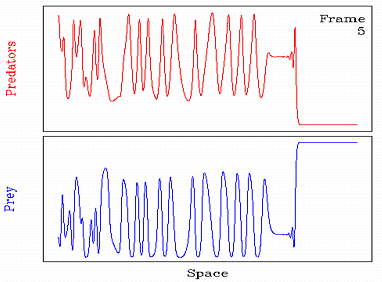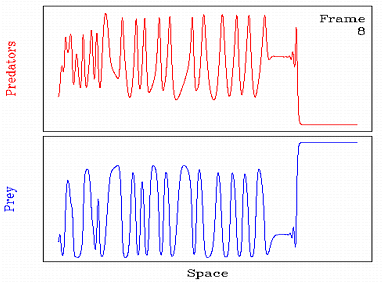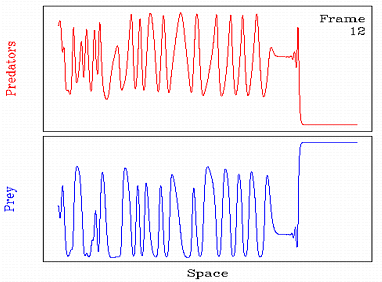
|
|
|
Мы говорили, что при моделировании биологических процессов используется метод индукции - от частного к общему, от гипотез. Именно таким образом строятся в биологии так называемые динамические модели популяций.
Популяция в биологии - это совокупность особей одного вида, существующих в одно и занимающих определенную территорию. Взаимодействие особей внутри популяции определяется внутривидовой конкуренцией, взаимодействие между популяциями - межвидовой конкуренцией.
Человечество как биологический вид можно также рассматривать как популяцию, причем популяцию с очень сложной внутривидовой конкуренцией, включающей множество иерархических уровней (экономическую, идеологическую, политическую, государственную, военную конкуренции).
Рассмотрим сначала простейшую модель роста населения.
Ni+1=Ni+aNi-bNi
Модель численности популяции с учетом внутривидовой конкуренции
Ni+1=(Ni+aNi-bNi)/(1+cNi)
Знаменатель отражает наличие внутривидовой конкуренции, делающей скорость роста тем меньше, чем больше численность популяции, с - параметр, характеризующий интенсивность внутривидовой конкуренции.
|
|