Рассмотрим простейшую из указанных моделей для вида с дискретными периодами размножения, в которой численность популяции в момент времени t равна Nt и изменяется во времени пропорционально величине основной чистой скорости воспроизводства R. Такими видами являются, например, большая часть растений, некоторые виды насекомых, у которых разные поколения четко разнесены во времени. Коэффициент R характеризует количество особей, которое воспроизводится в расчете на одну существующую, а также выживание уже существующих. Данная модель может быть выражена уравнением
| (1) |
решение которого имеет вид
| (2) |
где N0 - начальная численность популяции. Эта модель, однако, описывает популяцию, в которой отсутствует конкуренция и в которой R является константой; если R>1, то численность популяции будет бесконечно увеличиваться. В реальности в какой-то момент начинают работать механизмы сдерживания роста популяции. В литературе приводится немало интересных примеров быстрого роста численности популяций, если бы для их размножения существовали идеальные условия. Особенно это относится к насекомым, растениям и микроорганизмам, которые могли бы покрыть земной шар толстым слоем, если им создать благоприятные условия для размножения. Но в действительности такого роста популяций, когда их численность увеличивается в геометрической прогрессии, на сколько-нибудь длительных промежутках времени не наблюдается.
Следовательно, в первую очередь необходимо изменить уравнение (1) таким образом, чтобы чистая скорость воспроизводства зависела от внутривидовой конкуренции.
Конкуренцию можно определить как использование некоего ресурса (пищи, воды, света, пространства) каким-либо организмом, который тем самым уменьшает доступность этого ресурса для других организмов. Если конкурирующие организмы принадлежат к одному виду, то взаимоотношения между ними называют внутривидовой конкуренцией; если же они относятся к разным видам, то их взаимоотношения называют межвидовой конкуренцией.
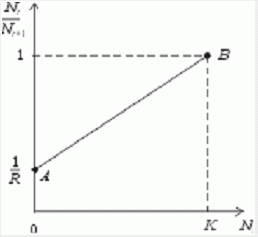
Рис. 1. К вопросу об ограничении скорости роста популяции
На рис. 1 показана простейшая возможная зависимость скорости воспроизводства от численности популяции. Точка A отражает ситуацию, в которой численность популяции близка к нулю, конкуренция при этом практически отсутствует, и фактическую скорость воспроизводства вполне можно описывать параметром R в его первоначальном виде. Следовательно, при низкой плотности популяции уравнение (1) вполне справедливо. В преобразованном виде оно выглядит так:
Точка B, напротив, отражает ситуацию, в которой численность популяции высока, и в значительной степени проявляется внутривидовая конкуренция. Фактическая скорость воспроизводства в результате конкуренции настолько снижена, что популяция в целом может не более чем восстанавливать в каждом поколении свою численность, потому что количество родившихся особей уравновешивается количеством погибших. Гипотезе, отраженной на рис. 1, соответствует уравнение
| (3) |
| где |
Это уравнение представляет собой модель роста популяции, ограниченного внутривидовой конкуренцией. Суть этой модели в том, что константа R в уравнении (1) заменена на фактическую скорость воспроизводства,
| т.е. |
которая уменьшается по мере роста численности популяции Nt. Достоинство полученного уравнения заключается в его простоте. Такой тип конкуренции приводит к саморегуляции численности популяции, изображенной на рис. 2 (для некоторого набора параметров модели; численное решение).
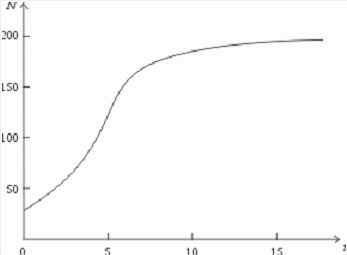
Рис. 2. Изменение численности популяции согласно уравнению (3) при R = 2, K = 200, N0 = 20
|
|