Серков А.Т., Серков А.А. Термодинамическая энтропия – это мера вероятности или превращение энергии?

ООО НИЦ (Научно-инженерный центр) «Углехимволокно»,
141 009. Московская обл., г. Мытищи, ул. Колонцова, д. 5.,
E-mail: arkady07@rambler.ru

Краткое содержание

Возникновение термодинамической энтропии рассмотрено на примере ионизации атома водорода, реакции образования молекулярного водорода и перехода вещества в газообразное состояние. При самопроизвольном процессе частица переходит на менее энергоёмкую орбиту со снижением потенциальной энергии, но повышением скорости и кинетической энергии. Термодинамическая энтропия – это прирост орбитальной кинетической энергии частиц вследствие повышения скорости, обусловленной переходом на низкопотенциальную орбиту. Эта энергия иммобилизована в виде орбитальной кинетической энергии. Она не доступна внешнему наблюдателю, но реально существует и закон сохранения энергии выполняется.

1. Введение

Понятие термодинамической энтропии ввел Р.Клаузиус, чтобы объяснить «исчезновение» части энергии в тепловых процессах. В соответствии с законом сохранения энергии (первое начало термодинамики) количество энергии в системе Q состоит из внутренней энергии U и работы системы pV (давление, объём).

Оно должно оставаться постоянным при изменении одной из составляющих. Фактически при самопроизвольно протекающих процессах оно уменьшается. Часть энергии превращается в некоторую другую составляющую термодинамическую функцию, которую Клаузиус назвал энтропия (превращение по-гречески). Уравнение (1) с внесённой энтропийной поправкой получило название второе начало термодинамики:

где Т – абсолютная температура, S – энтропия.

При таком подходе энтропия выражается формулой:

где q – приведенная тепловая энергия. Формула (3) не даёт возможности проводить количественный расчёт энтропии из-за неопределенности физического смысла величины q. Поэтому широкое распространение получило выражение энтропии, как меры вероятности протекания процесса:

где k – постоянная Больцмана, W – вероятность протекания процесса. Вероятность безразмерная величина. Чтобы придать рассчитываемой функции размерность энтропии, её умножают на постоянную, имеющую размерность энтропии Дж/К. Это делает получаемую величину условной и проводимый расчёт формальным, не отражающим физической сущности энтропии.

Сложившуюся ситуацию с определением термодинамического понятия энтропии представляется уместным охарактеризовать высказыванием одного из ведущих специалистов по данному вопросу [1]: «Термодинамическое определение энтропии часто кажется загадочным и произвольным».

По-видимому, физическое содержание понятия энтропия следует искать в элементарных энергетических актах (циклах), происходящих при взаимодействии в атомах и молекулах. Имеется в виду, например, выделение или поглощение энергии при переходе электрона с одной орбиты на другую или микрогравитационное взаимодействие молекул и их комплексов. Энергетический анализ таких взаимодействий оказался возможным после подтверждения гипотезы П.Лапласа «о видоизменении гравитационных сил в молекулярные при повышении плотности вещества»[2].

Речь идёт о явлении микрогравитация. Объекты микронных и нано размеров (атомы и молекулы), имеющие плотность ~ 10¹² г/см³, взаимодействуют между собой по обратно квадратичному гравитационному закону, но с необычно большой микрогравитационной константой равной 1,847·10²⁸ см³/гс². Пользуясь законами динамики орбитального движения, которые вытекают из закона гравитации, оказалось возможным рассчитать орбитальные расстояния, потенциальную и кинетическую энергию, а также энергию излучения при взаимодействии объектов указанных размеров. Всё это позволяет приблизиться к пониманию физической сущности термодинамического (энергетического) понятия энтропии.

2. Энтропия в элементарном энергетическом цикле в атоме

Рассмотрим энергетические превращения в цикле «ионизация – нейтрализация» на примере атома водорода. При ионизации электрон переводится с низшего энергетического уровня на высший, лежащий за пределами атома. Потенциальная энергия электрона повышается на величину энергии ионизации 13,6 эВ. Переход происходит с энергетического уровня Ер= - 13,6 эВ на нулевой уровень потенциальной энергии Ер= 0. При обратном переходе с энергетического уровня Ер= 0 на более низкий уровень Ер= -13,6 эВ, который протекает самопроизвольно, в соответствии с теоремой вириала (5) половина потенциальной энергии идёт на увеличение кинетической энергии электрона, а вторая на электромагнитное излучение:

Здесь Ер, Ек и Еи потенциальная, кинетическая и энергия излучения соответственно. Можно предположить, что проблема термодинамической энтропии скрыта в этих переходах. Если выделившаяся энергия излучения доступна для использования, то есть не исчезла, то кинетическая энергия орбитально движущегося электрона, обусловленная силами тяготения со стороны ядра, потеряна для внешнего наблюдателя. Она никак не может быть использована и больше всего подходит на роль «исчезнувшей» энергии, сиречь энтропии.

В приводимой ниже таблице 1 детализированы параметры рассмотренного энергетического цикла. В атоме водорода выбраны три энергетических уровня: уровень свободных электронов, лежащий за пределами поверхности атома при r > 110 пм; уровень, соответствующий вандерваальсову радиусу атома r = 110 пм и ионизационный уровень, находящийся при r = 4,167 пм. Как указывалось выше, микрогравитационная концепция [2] позволяет рассчитывать радиусы атома и привязывать к ним энергетические уровни в атоме. В графе 3 приведены справочные значения частот излучения, которые в соответствии с первоначальной теорией Бора являются частотами обращения электрона. Орбитальные радиусы обращения электрона рассчитывали по уравнению 3-го закона Кеплера, которое применительно к атому имеет вид [3]:

где ν- частота обращения (излучения) с^-1, g- константа микрогравитации равная 1,847·10²⁸ см³/гс^-2, m-масса протона 1,672·10^-24 г, r- орбитальный радиус. Для ионизационного уровня и поверхности атома орбитальный радиус соответственно равен 4,167 и 110,1 пм, см. столбец 4.

Таблица1. Параметры энергетического цикла в атоме водорода

Расчёт потенциальной энергии Ер проводили по классическому уравнению потенциальной энергии при орбитальном движении:

где g- константа микрогравитации, me- масса электрона равная 0,294·10^-24 г [2], m_p- масса протона 1,672·10^-24 г и r - орбитальный радиус. Полученные значения потенциальной энергии представлены в столбце 7 таблицы 1. Потенциальная энергия ионизационного уровня равна -13,58 эВ, поверхности атома -0,51 эВ, что практически совпадает с экспериментальными (справочными) данными, которые равны соответственно -13,60 и -0,38 эВ.

В графе 8 приведены результаты расчёта кинетической энергии для рассматриваемых энергетических уровней. Принято, что свободные электроны обладают нулевой кинетической энергией орбитального движения. Кинетическую энергию орбитального движения электрона в поверхностном слое и на ионизационном уровне рассчитывал по орбитальной скорости ( см. графу 5), которую в свою очередь определяли по уравнению орбитальной скорости:

где v_o- орбитальная скорость, g- постоянная микрогравитации, m_p - масса протона, r - орбитальный радиус.

Кинетическая энергия на ионизационном уровне равна 6,79 эВ и на поверхности атома 0,51 эВ, что в том и другом случае составляет 0,5Е_р. Следовательно, на обоих уровнях с высокой точностью выполняется уравнение (5) теоремы вириала. Вторая половина Е_р идёт на излучение, обусловленное пересечением силовых линий поля.

Кинетическая энергия орбитально движущегося электрона в отличие от энергии излучения никак не может быть использована, так как орбитальное движение строго задано параметрами силового центра (gm_p) согласно уравнению (8). По-существу, эта энергия выведена из обращения, так как находится в пределах атома. Тем не менее, она присутствует в системе и закон сохранения энергии соблюдается. Кинетическая энергия орбитально движущегося электрона иммобилизована тяготением ядра и потому является «исчезнувшей», то есть энтропийной составляющей общей энергии системы.

Кинетическая энергия орбитально обращающегося электрона может быть использована, если орбитальную скорость электрона повысить за счёт воздействия внешних сил тяготения или излучения до величины параболической скорости vp в соответствии с уравнением:

Для вывода электрона за пределы атома и преодоления сил тяготения орбитальную скорость электрона, находящегося на ионизационном уровне (r = 4,17 пм), необходимо повысить до уровня параболической скорости (1,217·10⁷ см/с),см.графу 6 таблицы1. В этом случае электрон становится «свободным электроном» и может быть использован для повторения энергетического цикла или для любых других целей (электронная проводимость, химические реакции и т.д.)

3. Энтропия при образовании молекулы водорода

Как было показано выше, под термодинамической энтропией следует понимать кинетическую энергию орбитально движущегося тела, которая «исчезла» поскольку контролируется силовым центром, вызывающим орбитальное движение и не доступна внешнему наблюдателю. Подобная ситуация наблюдается также при взаимодействии двух атомов водорода с образованием двухатомной молекулы водорода.

Атомы водорода имеют радиус ~ 110 пм. При сближении атомов происходит микрогравитационное взаимодействие их масс. По законам динамики орбитального движения атомы вступают в орбитальное движение друг относительно друга по типу двойных звёзд. Происходит сближение их ядер, уменьшается потенциальная энергия, наблюдается излучение электромагнитной энергии (тепловой эффект реакции), возрастает кинетическая энергия орбитально движущихся ядер и соответственно следует ожидать роста энтропии.

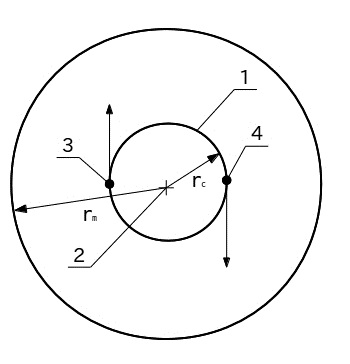
Схема модели молекулы водорода, состоящей из двух орбитально вращающихся атомов вокруг общего центра масс, представлена на рис.1. Протоны (ядра атомов) (3) и (4) под действием силы взаимного микрогравитационного тяготения обращаются по круговой орбите (1). Радиус орбиты rc= 36 пм. Обращение протонов происходит вокруг общего центра масс (2). Радиус молекулы rm= 146 пм. Он суммируется из полу суммы межъядерного расстояния и радиуса атома водорода. По порядку величины он близок к экспериментальному (справочному) значению равному 124 пм. Направление обращения протонов показано стрелками.

Рис.1. Схематическая модель молекулы водорода:
1- орбита движения протонов, 2 - центр масс,
3 - и 4 - орбитально движущиеся протоны, 5- граница молекулы.

Энергетика образования молекулы Н2 рассмотрена ранее [4], где приведено изменение потенциальной и кинетической энергии. При уменьшении межатомного расстояния с 157 до 71,2 пм согласно уравнению (7) потенциальная энергия уменьшается на 935 кДж/моль.

Следовательно, при таком сближении атомов с учётом уравнений (5) и (7) в виде излучения может выделиться 935/2 = 467,5 кДж/моль. Эта величина достаточно близка к экспериментальной (справочной) величине энергии связи Н-Н 436 кДж/моль, что подтверждает правильность подхода к рассмотрению проблемы.

Как следует из уравнения (5) уменьшение межатомного расстояния с 157 до 71,2 пм ведёт также к возрастанию кинетической энергии на 0,5Ер, то есть на 467,5 кДж/моль вследствие увеличения орбитальной скорости протонов. Такое повышение кинетической энергии обращающихся протонов подтверждается совпадением расчётной частоты обращения 0,1295·10¹⁵ с^-1 с характеристической ИК-частотой молекулярного водорода 0,1314·10¹⁵ с^-1. Это приращение кинетической энергии, как и в предыдущем рассмотренном примере, не доступно для внешнего наблюдателя, не детектируется по давлению или объёму. И в тоже время закон сохранения энергии соблюдается, так как кинетическая энергия внутри молекулы возросла. Следовательно, кинетическая энергия орбитального движения есть термодинамическая энтропия.

4. Энтропия газа

Ранее было показано [5], что вещества во всех трёх агрегатных состояниях имеют орбитальное движение составляющих их атомов и молекул. Для конденсированного состояния характерно орбитальное движение по замкнутым орбитам – круговым и эллиптическим, для газов по разомкнутым орбитам – параболическим и гиперболическим. Кинетическая энергия параболических и гиперболических орбит имеет две составляющих: энергию поступательного прямолинейного движения, первоначально сообщенного частице и кинетическую энергию, обусловленную силой микрогравитации. Мы полагаем, что предложенное определение энтропии, как орбитальной составляющей кинетической энергии движущейся частицы, справедливо также для движения по эллиптической, параболической и гиперболической орбите. Орбитальную составляющую кинетической энергии можно охарактеризовать по степени отклонения орбиты от прямолинейной траектории.

На рис.2 схематично приведены эллиптическая (1), параболическая (2) и гиперболическая (3) орбита движения частицы Р под действием силового центра О (6) в зависимости от первоначальной скорости частицы v0/. При скорости ниже параболической движение происходит по эллиптической орбите (1). Если v0 = 2gm/r, то частица имеет параболическую орбиту (2) и переходит в газовую фазу. При дальнейшем увеличении первоначальной скорости движение происходит по гиперболической орбите (3), которая ещё больше приближается к прямолинейной траектории.

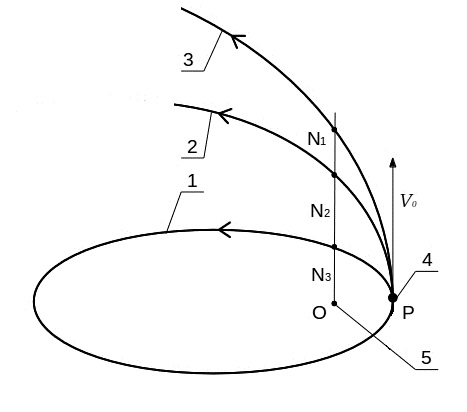
Рис.2. Схема движения частицы Р по эллиптической (1), параболической (2) и гиперболической (3) орбите. Орбитальная частица Р с начальной скоростью v₀ (4), силовой центр gm (5).

Отклонение от прямолинейной траектории, характеризующее орбитальную составляющую скорости и соответственно кинетической энергии частицы, обычно выражают эксцентриситетом орбиты. На рис.2 эксцентриситет орбит можно представить отношением отрезков:

Чем больше эксцентриситет, тем меньше влияние силового центра и соответственно меньше орбитальная составляющая кинетической энергии и меньше энтропия. При движении по прямой траектории энтропийная составляющая отсутствует полностью.

«Исчезновение» энтропийной составляющей кинетической энергии при малом эксцентриситете объясняется ударом молекулы о стенку под углом. Это соответственно приводит к заниженным значениям давления и произведений рV по сравнению с теоретическими, предписываемыми молекулярно-кинетической теорией.

Выводы

1. При переходе электрона в атоме водорода с орбиты r > 110 пм на орбиту r = 4,167 пм потенциальная энергия снижается с 0 до -13,58 эВ при этом половина потенциальной энергии 6,79 эВ реализуется в виде электромагнитного излучения, а вторая половина в количестве 6,79 эВ идёт на повышение орбитальной кинетической энергии электрона. Последняя не зависит от внешнего наблюдателя, «исчезает» для него, хотя реально она в системе присутствует, и закон сохранения энергии соблюдается. На основании сказанного можно полагать, что кинетическая энергия орбитального движения является термодинамической энтропией.

2.При образовании молекулы водорода сближение атомов водорода в пределах от 157 до 72 пм ведёт к реализации потенциальной энергии в объёме 935 кДж/моль. Из этого количества 50%,то есть 467,5 кДж/моль выделяется в виде электромагнитного излучения, что практически совпадает с величиной теплового эффекта реакции образования молекулярного водорода, равного 436 кДж/моль. Вторая половина потенциальной энергии 467,5 кДж/моль идёт на увеличение орбитальной кинетической энергии обращения протонов по круговой орбите вокруг общего центра масс. Это подтверждается совпадением расчётной частоты обращения 0,1295·10¹⁵ с^-1 с характеристической ИК-частотой молекулярного водорода 0,1314·10¹⁵ с^-1.

3. В газовом агрегатном состоянии, когда движение частиц осуществляется по разомкнутым параболическим и гиперболическим орбитам, энтропия представляет собой орбитальную составляющую кинетической энергии частиц. Эту составляющую предлагается характеризовать по отклонению движения частицы от прямолинейной траектории по эксцентриситету орбиты.

В заключение хотелось бы отметить большую проницательность Р. Клаузиуса, предсказавшего необходимость введения в закон сохранения функции (энтропии), учитывающей фиктивное исчезновение энергии. Такой функцией оказалась орбитальная кинетическая энергия атомов и молекул. Верификация этой функции оказалась возможной только после установления атомно-молекулярного строения вещества и микрогравитационного взаимодействия атомов и молекул, включая их орбитальное движение, относительно друг друга.

Литература

1. П. Эткинс, Физическая химия,!980, М. Изд. «Мир», т.1, стр.146

2. А.Т. Серков, А.А. Серков, Микрогравитация, электричество, силы притяжения и отталкивания в атоме, http://www.sciteclibrary.ru/rus/catalog/pages/12915.html

3. А.Т. Серков, А.А. Серков, Зависимость длины волны характеристического рентгеновского излучения химических элементов от их атомных радиусов и масс (3-ий закон Кеплера в атомных системах),

4. А.Т. Серков, А.А. Серков, Энергия химических и межмолекулярных связей, http://sciteclibrary.ru/rus/catalog/pages/12235.html

5. А.Т. Серков, В.Н. Покровский А.А. Серков, О предстоящей смене научной парадигмы в физике, http://www.sciteclibrary.ru/rus/catalog/pages/10375.html

Знаете ли Вы, что в 1965 году два американца Пензиас (эмигрант из Германии) и Вильсон заявили, что они открыли излучение космоса. Через несколько лет им дали Нобелевскую премию, как-будто никто не знал работ Э. Регенера, измерившего температуру космического пространства с помощью запуска болометра в стратосферу в 1933 г.? Подробнее читайте в FAQ по эфирной физике.

№ п.п.	Наименование уровня	Частота, ν·10^-15с^-1	Радиус, r. пм	vо·10^-7, см/с	vp·10^-7, см/с	- Ер, эВ	Ек, эВ	Еи, эВ
1	2	3	4	5	6	7	8	9
1	Свободные электроны	0	> 110	0	0	0	0	0
2	Поверхность атома	0,0242	110,1	0,1675	0,2368	0,5147	0,2574	0,2573
3	Ионизационный уровень	3,2874	4,167	0,8604	1,217	13,58	6,793	6,787