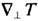Эттингсхаузена эффект. РЕАЛЬНАЯ ФИЗИКА. Глоссарий по физике

Эттингсхаузена эффект - возникновение поперечного градиента температуры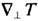

в проводнике с током, помещённом в магн. поле Н. Открыт в 1886 А. Эттингсхаузеном (A. Ettingshausen). В изотропном образце -

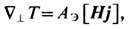
где j-плотность электрич. тока; А_Э - коэф. Эттингсха-узена.

Эттингсхаузена эффект обусловлен разделением траекторий носителей заряда (переносящих ток j) Лоренца силой. Сила, действующая на носители заряда в магн. поле, в среднем компенсируется электрич. полем Холла (см. Холла эффект ).Полная компенсация имеет место лишь для носителей заряда, движущихся с нек-рой ср. скоростью; траектории более быстрых (горячих) носителей заряда отклоняются к одной стороне образца, более медленных (холодных) - к противоположной, что и приводит к возникновению градиента температуры поперёк образца. Знак Э. э. не зависит от знака носителей.

В вырожденных полупроводниках ток переносят носители с энергиями, лежащими в слое шириной ~kT вблизи энергии Ферми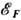

. Коэф. А_Э при этом порядка kT/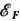

, т. е. мал. При смешанной проводимости возникает биполярный вклад в Э. э., связанный с совместным движением электронов и дырок, и А_Э сильно возрастает (~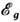

/kT, где

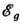- ширина запрещённой зоны). В случае низких температур коэф. А_Э содержит вклад, связанный с эффектом увлечения электронов фононами, а в квантующих магн. полях он должен испытывать квантовые осцилляции.

Эттингсхаузена эффект применяется в термоэлементах, основанных на эффекте Пельтье и используемых для термоэлектрич. охлаждения: приложение сильного магн. поля к термоэлементу из полупроводника с собств. проводимостью (напр., сплава Bi-Sb) обеспечивает высокую эффективность охлаждения за счёт большой величины А_Э.

Литература по эффекту Эттингсхаузена

Знаете ли Вы, что, как и всякая идолопоклонническая религия, релятивизм ложен в своей основе. Он противоречит фактам. Среди них такие:

1. Электромагнитная волна (в религиозной терминологии релятивизма - "свет") имеет строго постоянную скорость 300 тыс.км/с, абсурдно не отсчитываемую ни от чего. Реально ЭМ-волны имеют разную скорость в веществе (например, ~200 тыс км/с в стекле и ~3 млн. км/с в поверхностных слоях металлов, разную скорость в эфире (см. статью "Температура эфира и красные смещения"), разную скорость для разных частот (см. статью "О скорости ЭМ-волн")

2. В релятивизме "свет" есть мифическое явление само по себе, а не физическая волна, являющаяся волнением определенной физической среды. Релятивистский "свет" - это волнение ничего в ничем. У него нет среды-носителя колебаний.

3. В релятивизме возможны манипуляции со временем (замедление), поэтому там нарушаются основополагающие для любой науки принцип причинности и принцип строгой логичности. В релятивизме при скорости света время останавливается (поэтому в нем абсурдно говорить о частоте фотона). В релятивизме возможны такие насилия над разумом, как утверждение о взаимном превышении возраста близнецов, движущихся с субсветовой скоростью, и прочие издевательства над логикой, присущие любой религии.

4. В гравитационном релятивизме (ОТО) вопреки наблюдаемым фактам утверждается об угловом отклонении ЭМ-волн в пустом пространстве под действием гравитации. Однако астрономам известно, что свет от затменных двойных звезд не подвержен такому отклонению, а те "подтверждающие теорию Эйнштейна факты", которые якобы наблюдались А. Эддингтоном в 1919 году в отношении Солнца, являются фальсификацией. Подробнее читайте в FAQ по эфирной физике.