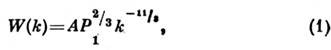
Стационарные неравновесные распределения частиц или волн по импульсам (волновым числам) - распределения, обращающие в нуль интеграл столкновений в кинетическом уравнении и полностью определяющиеся постоянным в пространстве импульсов (волновых чисел) потоком сохраняющихся величин, напр. энергии, импульса, числа частиц (или волнового действия для квазичастиц). С. н. р. называются также колмогоровскими спектрами (КС).
Впервые А. Н. Колмогоровым и А. М. Обуховым (1941) в теории турбулентности несжимаемой жидкости было построено в интервале масштабов, промежуточных
между масштабами возбуждаемых и эффективно затухающих движений, универсальное
С. н. р. энергии по волновым числам k - W(k) - известный КС гидродинамич.
турбулентности:
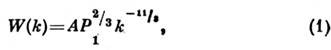
где А - константа, Р1 - интегральный поток энергии по спектру волновых чисел k.
При выводе ф-лы (1) использована гипотеза о локальности турбулентности, т. е. о том, что существенно взаимодействуют между собой только волновые движения с размерами одного порядка. Эта гипотеза для турбулентности в несжимаемой жидкости (сильная турбулентность) строго не доказана.
В физ. средах, в к-рых взаимодействие волн или частиц можно описать кинетич. ур-ниями для квазичастиц или частиц, нахождение С. н. р. сводится к решению кинетич. ур-ний. В этом случае локальность С. н. р. соответствует сходимости интеграла столкновений.
Подобно термодинамически равновесным распределениям С. н. р. обращают в нуль интеграл столкновений, однако они существуют только при наличии потока к--л. сохраняющейся величины в импульсном пространстве, поддерживаемом источником и стоком. Начиная со слаботурбулентных С. н. р. (КС) волн, полученных В. Е. Захаровым (1965), идея об эстафетной передаче по масштабам интегралов движения (сохраняющихся величин) была широко использована при рассмотрении турбулентности в плазме, твёрдом теле, жидкости; были получены изотропные и анизотропные С. в. р. (КС), соответствующие переносу постоянных в импульсном пространстве (или пространстве волновых чисел) потоков энергии, импульса, числа частиц, волнового действия.
Стационарные неравновесные распределения (колмогоровские спектры)
волн с распадныи законом дисперсии. Если дисперсия волн к--л. одного
типа описывается распадными условиями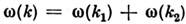
, то интеграл столкновений
,
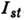получаемый усреднением динамич. ур-ний, может быть записан следующим образом:
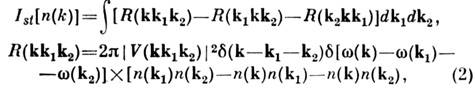
где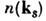
- плотность числа квазичастиц,
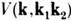- матричный элемент трёхволнового взаимодействия,
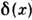- дельта-функция. В однородной и изотропной среде при масштабной инвариантности закона дисперсии и матричного элемента относительно своих аргументов,
а именно
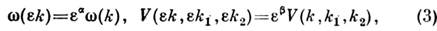
С. н. р. числа квазичастиц по волновым числам n(k), обращающее
в нуль интеграл столкновений (2) и соответствующее пост. потоку энергии
Р1, имеет вид:
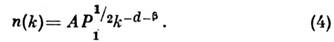
В ур-ниях (3) и (4) Л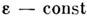 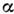и
,
и
- константы, характеризующие степень однородности закона дисперсии и матричного
элемента, d - размерность волновых векторов.
Так, напр., для капиллярных волн на поверхности жидкости d = 2,
и локальное изотропное С. н. р. числа квазичастиц, соответствующее пост.
потоку энергии P1 имеет вид:
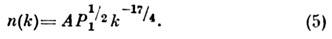
В среде, обладающей аксиальной симметрией относительно выделенного направления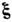
,
при определённой масштабной инвариантности закона дисперсии и матричного
элемента трёхволнового взаимодействия, а именно
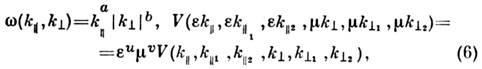
анизотропное С. н. р. числа квазичастиц по волновым векторам, соответствующее
пост. потоку импульса R в направлении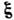
,
имеет вид:
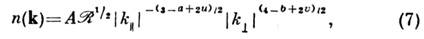
где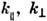
- компоненты волнового вектора, соответственно параллельная и перпендикулярная
.
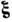В частности, для ионно-звуковых колебаний в плазме, помещённой в
направленное по оси х сильное магн. поле (а = 1, b
= 2, и = 3/2, v = 0), локальное анизотропное
С. н. р. числа квазичастиц
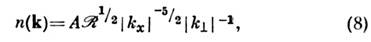
где
- поток импульса, направленный по оси х. Локальные анизотропные
С. н. р. получены для бездивергентных волн Росби, косых электронно-дрейфовых,
ионно-дрейфовых, электронно-звуковых, магнитозвуковых, альвеновских волн
в плазме, волн плотности в гравитирующих астрофиз. объектах.
Стационарные неравновесные распределения волн с нераспадным законом
дисперсии. В случае дисперсии волн, не описываемой распадными условиями,
интеграл столкновений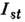
может
быть записан следующим образом:
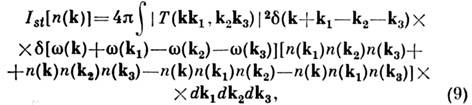
где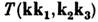
- матричный элемент взаимодействия.
В однородной и изотропной среде при аналогичной выражению (3) масштабной
инвариантности закона дисперсии и матричного элемента относительно своих
аргументов С. н. р. числа квазичастиц по волновым числам, соответствующее
пост. потоку энергии P1 (или волнового действия Р0), имеет вид:
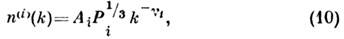
где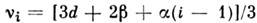
, Ai - константы, i = 0, 1 соответствует пост. потоку
волнового действия, энергии. Так, напр., для гравитац. волн на поверхности
глубокой жидкости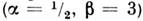
имеются локальные С. н. р. числа квазичастиц, соответствующие пост. потоку
энергии в область больших волновых чисел (v1 = 4), т.
е. передаче энергии от больших масштабов к малым, и пост. потоку волнового
действия в область малых волновых чисел (v0 = 23/6),
т. е. от малых масштабов к большим.
Стационарные неравновесные распределения частиц. Интеграл столкновений
Больцмана Ist может быть записан следующим образом:
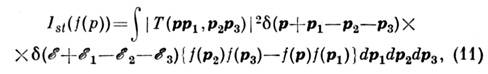
где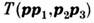
- матричный элемент взаимодействия частиц,
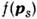- функция распределения частиц,
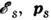- соответственно энергия, импульс s-й частицы.
В однородной и изотропной среде при масштабной инвариантности зависимости
энергии от импульса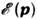
и матричного элемента относительно своих аргументов, а именно
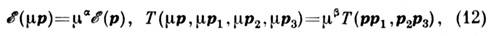
С. н. р. частиц по импульсу, соответствующее пост. потоку энергии Р1(i
= 1) или пост. потоку частиц Р0(i = 0),
имеет вид:
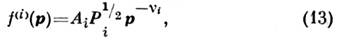
где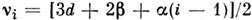
, i = 0, 1.
Так, для нерелятивистских заряж. частиц, взаимодействующих по закону
Кулона с учётом статической экранировки
, имеется локальное С. н. р. частиц, соответствующее пост. потоку энергии
в импульсном пространстве (v1 = +5/2). Именно это С.
н. р. обращает в нуль также интеграл столкновений в квантовой форме
(см. Кинетические
уравнения для плазмы).
В. И. Карась
|
|
 |
