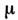 и оператором числа частиц N величина С. п.
и оператором числа частиц N величина С. п.
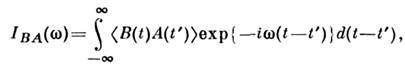
Спектральная плотность (спектральная интенсивность) в статистической физике - коэффициенты разложения временных корреляционных функций в
интеграл Фурье. Для операторов А к В квантовомеханич. системы с
гамильтонианом
Н, хим. потенциалом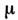 и оператором числа частиц N величина С. п.
и оператором числа частиц N величина С. п.
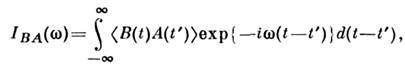
где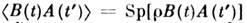 - зависящая лишь от (t - t')равновесная временная корреляц. функция
двух операторов
- зависящая лишь от (t - t')равновесная временная корреляц. функция
двух операторов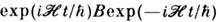 в Гейзенберга представлении
в Гейзенберга представлении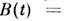
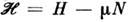
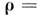
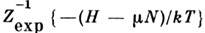 - статистич. оператор для большого канонического распределения Гиббса,
Z =
- статистич. оператор для большого канонического распределения Гиббса,
Z =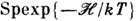 , Sp обозначает суммирование диагональных матричных элементов оператора.
С. п. можно получить из спектральных представлений Грина функции, что
затем позволяет вычислить временные корреляц. функции. В том случае, когда
А и В эрмитово сопряжённые операторы
, Sp обозначает суммирование диагональных матричных элементов оператора.
С. п. можно получить из спектральных представлений Грина функции, что
затем позволяет вычислить временные корреляц. функции. В том случае, когда
А и В эрмитово сопряжённые операторы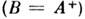 ,
величина . Перестановочность операторов под знаком Sp
,
величина . Перестановочность операторов под знаком Sp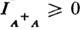 определяет условие Кубо - Мартина-Швингера (R. Kubo, P. С. Martin, J. Schwinger,
1959) для С. п.:
определяет условие Кубо - Мартина-Швингера (R. Kubo, P. С. Martin, J. Schwinger,
1959) для С. п.: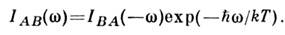
В более явной форме С. п. можно представить в виде суммы по всем собств.
состояниям оператора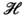 (т и п - квантовые числа):
(т и п - квантовые числа):

Здесь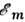 и
и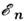 - собств.
значения оператора
- собств.
значения оператора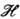 ,
, и
и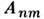 - матричные элементы операторов А и В по системе собств.
функций
- матричные элементы операторов А и В по системе собств.
функций -
дельта-функция .Для систем, изучаемых в статистич. физике, спектр
-
дельта-функция .Для систем, изучаемых в статистич. физике, спектр практически непрерывен из-за больших размеров системы в термодинамическом
пределе, поэтому суммированию по т, п соответствует интегрирование
по плотности состояний. В силу этого С. п. проявляет
практически непрерывен из-за больших размеров системы в термодинамическом
пределе, поэтому суммированию по т, п соответствует интегрирование
по плотности состояний. В силу этого С. п. проявляет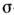 -образный
характер лишь для систем с незатухающими элементарными возбуждениями (напр.,
для идеального газа квазичастиц).
-образный
характер лишь для систем с незатухающими элементарными возбуждениями (напр.,
для идеального газа квазичастиц).
В случае классич. статистич. механики А и В - соответствующие операторам динамические переменные, а операция Sp переходит в интегрирование по всем координатам и импульсам чаетиц и суммирование по числу частиц.
С. п. может быть вычислена точно лишь для простейших модельных систем, однако при её приближённом нахождении для сложных систем должны выполняться нек-рые точные интегральные соотношения - т. н. правила сумм ,к-рые служат критерием правильности выполненных аппроксимаций.

Когда тот или иной физик использует понятие "физический вакуум", он либо не понимает абсурдности этого термина, либо лукавит, являясь скрытым или явным приверженцем релятивистской идеологии.
Понять абсурдность этого понятия легче всего обратившись к истокам его возникновения. Рождено оно было Полем Дираком в 1930-х, когда стало ясно, что отрицание эфира в чистом виде, как это делал великий математик, но посредственный физик Анри Пуанкаре, уже нельзя. Слишком много фактов противоречит этому.
Для защиты релятивизма Поль Дирак ввел афизическое и алогичное понятие отрицательной энергии, а затем и существование "моря" двух компенсирующих друг друга энергий в вакууме - положительной и отрицательной, а также "моря" компенсирующих друг друга частиц - виртуальных (то есть кажущихся) электронов и позитронов в вакууме.
Однако такая постановка является внутренне противоречивой (виртуальные частицы ненаблюдаемы и их по произволу можно считать в одном случае отсутствующими, а в другом - присутствующими) и противоречащей релятивизму (то есть отрицанию эфира, так как при наличии таких частиц в вакууме релятивизм уже просто невозможен). Подробнее читайте в FAQ по эфирной физике.
|
|