Уравнение Пирогова - дифференциальное ур-ние, описывающее
эволюцию распределения вероятностей для пространственного положения броуновской
частицы. Пусть w(x,t) - плотность вероятности того, что броуновская
частица (см. Броуновское движение)в момент времени t находится
в точке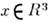 Тогда
в предположении, что на эту частицу действует переменное силовое поле K(x,t), плотность w удовлетворяет следующему дифференциальному ур-нию:
Тогда
в предположении, что на эту частицу действует переменное силовое поле K(x,t), плотность w удовлетворяет следующему дифференциальному ур-нию: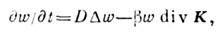 где
где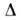 -
Лапласа
оператор, D и
-
Лапласа
оператор, D и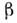 - параметры, определяемые массой частицы, вязкостью, температурой среды и т.
д.
- параметры, определяемые массой частицы, вязкостью, температурой среды и т.
д.
Это ур-ние впервые было выведено Пироговым и явилось прообразом
более общих дифференциальных ур-ний в теории марковских диффузионных процессов
(Фоккера
- Планка уравнение, Колмогорова уравнения).
Знаете ли Вы, в чем фокус эксперимента Майкельсона?
Эксперимент А. Майкельсона, Майкельсона - Морли - действительно является цирковым фокусом, загипнотизировавшим физиков на 120 лет.
Дело в том, что в его постановке и выводах произведена подмена, аналогичная подмене в школьной шуточной задачке на сообразительность, в которой спрашивается:
- Cколько яблок на березе, если на одной ветке их 5, на другой ветке - 10 и так далее
При этом внимание учеников намеренно отвлекается от того основополагающего факта, что на березе яблоки не растут, в принципе.
В эксперименте Майкельсона ставится вопрос о движении эфира относительно покоящегося в лабораторной системе интерферометра. Однако, если мы ищем эфир, как базовую материю, из которой состоит всё вещество интерферометра, лаборатории, да и Земли в целом, то, естественно, эфир тоже будет неподвижен, так как земное вещество есть всего навсего определенным образом структурированный эфир, и никак не может двигаться относительно самого себя.
Удивительно, что этот цирковой трюк овладел на 120 лет умами физиков на полном серьезе, хотя его прототипы есть в сказках-небылицах всех народов всех времен, включая барона Мюнхаузена, вытащившего себя за волосы из болота, и призванных показать детям возможные жульничества и тем защитить их во взрослой жизни. Подробнее читайте в FAQ по эфирной физике.
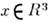 Тогда
в предположении, что на эту частицу действует переменное силовое поле K(x,t), плотность w удовлетворяет следующему дифференциальному ур-нию:
Тогда
в предположении, что на эту частицу действует переменное силовое поле K(x,t), плотность w удовлетворяет следующему дифференциальному ур-нию: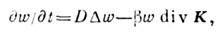 где
где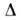 -
Лапласа
оператор, D и
-
Лапласа
оператор, D и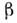 - параметры, определяемые массой частицы, вязкостью, температурой среды и т.
д.
- параметры, определяемые массой частицы, вязкостью, температурой среды и т.
д.

