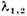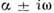=
;
а < 0 (а) и а > 0 (б).
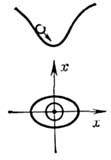
Равновесия состояние динамической системы - состояние динамической системы, к-рое не изменяется во времени. Состояние равновесия динамической системы может быть устойчивым, неустойчивым и безразлично-устойчивым. Движение системы вблизи равновесия (при малом от него отклонении) существенно различается в зависимости от характера (типа) состояния равновесия динамической системы. В случае систем с одной степенью свободы, если состояние равновесия динамической системы устойчиво, то при малом возмущении (отклонении) система возвращается к нему, совершая затухающие колебания (на фазовой плоскости такому движению соответствует устойчивый фо-кус - рис. 1, а)или двигаясь апериодически (устойчивый узел - рис. 2, а). Вблизи неустойчивого состояния равновесия динамической системы малые отклонения системы нарастают, при этом система совершает колебания (неустойчивый фокус - рис. 1, б)или движется апериодически (неустойчивый узел - рис. 2, б); вблизи седлового состояния равновесия динамической системы (рис. 3) возможно вначале приближение к состоянию равновесия динамической системы, а затем уход от него. Наконец, в случае безразлично-устойчивого состояния равновесия динамической системы ("центр", рис. 4) малые отклонения приводят к незатухающим колебаниям вблизи состояния равновесия динамической системы. Для систем с неск. степенями свободы движение системы вблизи состояния равновесия динамической системы может быть более сложным и существенно зависит от характера начального отклонения.
Рис. 1. Поведение траекторий в окрестности устойчивого
(а) и неустойчивого (б) фокусов; здесь n = 2, =;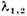
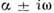а < 0 (а) и а > 0 (б).
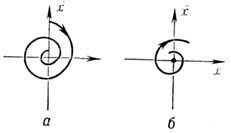
Рис. 2. Траектории в окрестности устойчивого
(а) и неустойчивого (б) узлов; l2 < l1
< О (а), 0 < l2 < l1
(6).
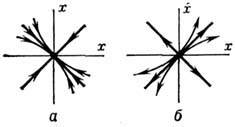
Рис. 3. Состояние равновесия типа "седло".
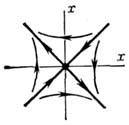
рис. 4. Замкнутые траектории в
окрестности точки типа "центр".
Движение динамич. системы вблизи состояния равновесия динамической системы чаще всего
описывается линеаризов. ур-ниями, имеющими решение в виде сумм экспонент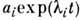 
с комплексными (в общем случае) характеристич.
показателями li - корнями характеристич. ур-ния:
det(A-lE)=0, где
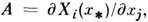а Xi - правая часть дифференц. ур-ний,
описывающих исследуемую систему:
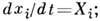
х* - решение, отвечающее равновесию,
Х(х*)= 0. Если Relk < 0 (Relk
> 0), то состояние равновесия динамической системы асимптотически устойчиво (неустойчиво) и через все точки в
окрестности х* проходят траектории, стремящиеся к x* при t : , (t : -,),- рис. 1.
Если Relk < 0, k=1,...,
т, Relk> 0, j = = т + 1, ..., n,
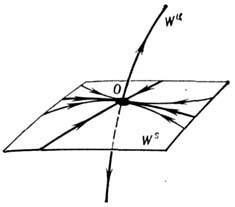
то состояние равновесия динамической системы - "седло"; траектории, стремящиеся к нему при t :
, (t : -,), лежат на устойчивом (неустойчивом) многообразии
- многомерной сепаратрисе размерности т (п - т) - рис. 5.
Рис. 5. "Седло" в трёхмерном фазовом
пространстве; l2 < < l1 < 0, l3
> 0; WS - двумерное устойчивое, WU -
одномерное неустойчивое многообразия.
В консервативных (в частности, гамильтоновых)
динамич. системах устойчивыми (по Ляпунову) могут быть лишь
состояния равновесия динамической системы чисто мнимыми
или нулевыми lk, . Например, незатухающие колебания шарика
в "потенциальной яме" (рис. 4) описываются движением точки по замкнутой
траектории в окрестности состояния равновесия динамической системы типа "центр", для к-рого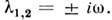
Если динамич. система зависит от параметра, то (даже и в неконсервативном случае) при его изменении Relk может обратиться в нуль, и тогда состояние равновесия динамической системы может претерпевать бифуркации, связанные с потерей (приобретением) устойчивости или с изменением размерности его сепаратрис (см. также Устойчивость движения).
В. С. Афраймович, М. И. Рабинович
Релятивисты и позитивисты утверждают, что "мысленный эксперимент" весьма полезный интрумент для проверки теорий (также возникающих в нашем уме) на непротиворечивость. В этом они обманывают людей, так как любая проверка может осуществляться только независимым от объекта проверки источником. Сам заявитель гипотезы не может быть проверкой своего же заявления, так как причина самого этого заявления есть отсутствие видимых для заявителя противоречий в заявлении.
Это мы видим на примере СТО и ОТО, превратившихся в своеобразный вид религии, управляющей наукой и общественным мнением. Никакое количество фактов, противоречащих им, не может преодолеть формулу Эйнштейна: "Если факт не соответствует теории - измените факт" (В другом варианте " - Факт не соответствует теории? - Тем хуже для факта").
Максимально, на что может претендовать "мысленный эксперимент" - это только на внутреннюю непротиворечивость гипотезы в рамках собственной, часто отнюдь не истинной логики заявителя. Соответсвие практике это не проверяет. Настоящая проверка может состояться только в действительном физическом эксперименте.
Эксперимент на то и эксперимент, что он есть не изощрение мысли, а проверка мысли. Непротиворечивая внутри себя мысль не может сама себя проверить. Это доказано Куртом Гёделем.
Понятие "мысленный эксперимент" придумано специально спекулянтами - релятивистами для шулерской подмены реальной проверки мысли на практике (эксперимента) своим "честным словом". Подробнее читайте в FAQ по эфирной физике.
|
|
 |
