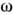 ,n),
к-рая определяет ср. поток энергии dS через площадку da, сосредоточенный
в телесном угле
,n),
к-рая определяет ср. поток энергии dS через площадку da, сосредоточенный
в телесном угле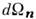 вблизи направления и и в интервале частот
вблизи направления и и в интервале частот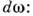 dS =
dS =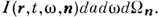 Поэтому ср. плотность потока энергии S в точке r в момент
времени t равна:
Поэтому ср. плотность потока энергии S в точке r в момент
времени t равна:
Перенос излучения - распространение эл--магн. излучения, звука, нейтронов и др. частиц в различных средах:
в свободном пространстве, в регулярно-неоднородных и случайно-неоднородных
(турбулентных) средах, в средах с дискретными рассеивателями и т. д. при
наличии процессов поглощения, испускания и рассеяния. Традиционно П. и.
рассматривают в разл. разделах оптики, в частности при описании фотометрич.
измерений, выяснении условий формирования оптич. изображений, нахождении
характеристик рассеянного излучения и др. Классич. теория П. и. получена
из энергетич. соображений и служит основой фотометрии .Кроме того,
теорию П. и. применяют в астрофизике при расчёте светимости звёзд, в теплофизике
при анализе теплопередачи через излучение, в геофизике при изучении теплового
баланса Земли, а также в акустике, теории плазмы и ядерной физике. Начало
теоретич. фотометрии и теории П. и. как раздела науки связывают обычно
с именами П. Бугера (P. Bouguer) и И. Ламберта (J. Lambert). Применительно
к рассеивающим средам основы теории П. и. заложили О. Д. Хвольсон (1890)
и А. Шустер (A. Schuster, 1905). Фотометрия оперирует с энергетич. характеристиками,
описывающими отклик квадратичных приёмников излучения. Классич. феноменологич.
теория П. и. использует наглядные понятия лучевой оптики, дополненные статистич.
предположением о полной взаимной некогерентности полей для лучей, имеющих
разные направления. Это предположение позволяет суммировать ср. интенсивности
лучей, приходящих с разл. направлений, игнорируя фазовые соотношения (аналогичное
допущение в нелинейной теории волн известно как приближение случайных фаз).
Совр. теория П. и. основывается на статистико-волновом
подходе, когда излучение и среда трактуются как два взаимодействующих случайных
поля и излучение считается статистически квазиоднородным.
Основные понятия. В классич. теории
переноса скалярного излучения в свободном пространстве, рассматривающей
волновое поле как совокупность некогерентных лучевых пучков, осн. понятием
является спектральная яркость I = I(r,t,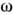 ,n),
к-рая определяет ср. поток энергии dS через площадку da, сосредоточенный
в телесном угле
,n),
к-рая определяет ср. поток энергии dS через площадку da, сосредоточенный
в телесном угле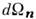 вблизи направления и и в интервале частот
вблизи направления и и в интервале частот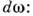 dS =
dS =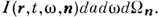 Поэтому ср. плотность потока энергии S в точке r в момент
времени t равна:
Поэтому ср. плотность потока энергии S в точке r в момент
времени t равна:
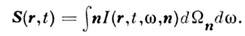
Ср. плотность энергии поля равна:
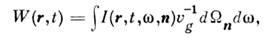
где vg - групповая скорость
распространения излучения. Эти соотношения сохраняют силу и для разреженных
рассеивающих сред.
Основой волновой теории П. и. служит интегродифференц.
ур-ние переноса излучения. Для неизменной во времени статистически однородной
рассеивающей среды оно имеет вид:
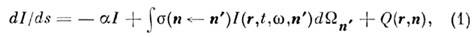
где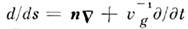 - производная вдоль луча, Q - функция источников,
- производная вдоль луча, Q - функция источников,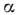 и
и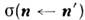 - феноменологич.
параметры, наз. коэффициентом экстинкции и сечением рассеяния из направления
п' в направление п. Ур-ние (1) с соответствующими нач. и граничными
условиями определяет поведение яркости I. Эта задача привела к формированию
самостоят. ветви матем. физики - матем. теории П. и.
- феноменологич.
параметры, наз. коэффициентом экстинкции и сечением рассеяния из направления
п' в направление п. Ур-ние (1) с соответствующими нач. и граничными
условиями определяет поведение яркости I. Эта задача привела к формированию
самостоят. ветви матем. физики - матем. теории П. и.
Ур-нпе (1) выражает баланс энергии в бесконечно
малом объёме среды: скорость изменения яркости I вдоль луча определяется
рассеянием в данное направление п со всех др. направлений n'
(интегральный член) и ослаблением из-за рассеяния и поглощения (член -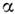 I).
Коэф. экстинкции
I).
Коэф. экстинкции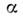 выражается в виде суммы,
выражается в виде суммы,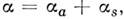 энергетич. коэффициента поглощения среды
энергетич. коэффициента поглощения среды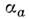 и коэффициента рассеяния
и коэффициента рассеяния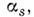 связанного с сечением рассеяния соотношением
связанного с сечением рассеяния соотношением
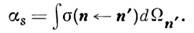
Вне области источников выполняется ур-ние интегрального энергетич. баланса
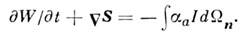
Для квазиоднородных и квазистацпонарных
сред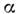 и
и зависят
от r и t. В случае рассеяния с изменением частоты в интегральном
члене в (1) появляется дополнит. интегрирование по частоте. При учёте векторного
характера эл--магн. поля яркость I нужно заменить на яркостную матрицу,
к-рая описывает не только интенсивность, но и поляризац. свойства излучения,
причём
зависят
от r и t. В случае рассеяния с изменением частоты в интегральном
члене в (1) появляется дополнит. интегрирование по частоте. При учёте векторного
характера эл--магн. поля яркость I нужно заменить на яркостную матрицу,
к-рая описывает не только интенсивность, но и поляризац. свойства излучения,
причём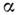 и
и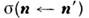 также
становятся матричными величинами. Скалярное ур-ние (1) используют в оптике
для описания светового излучения в тех случаях, когда можно пренебречь
поляризац. эффектами. Аналогичные ур-ния с нелинейной правой частью используют
при описании эл--магн. излучения в плазме (т. н. кинетич. ур-ния для волн).
также
становятся матричными величинами. Скалярное ур-ние (1) используют в оптике
для описания светового излучения в тех случаях, когда можно пренебречь
поляризац. эффектами. Аналогичные ур-ния с нелинейной правой частью используют
при описании эл--магн. излучения в плазме (т. н. кинетич. ур-ния для волн).
Поскольку ур-ние (1) основано на лучевых
понятиях, в нём акцентируется лишь корпускулярная сторона дуализма волна
- частица. Поэтому ур-ние (1) служит также основой теории переноса нейтронов,
где вместо яркости I фигурирует одночастичная функция распределения
нейтронов по скоростям, а ур-ние аналогично линеаризованному кинетическому
уравнению Болъцмана. При квантовой интерпретации излучения яркость
I
пропорциональна функции распределения фотонов по направлениям и по частотам.
Обоснование теории П. и. было достигнуто
в рамках статистич. оптики, к-рая ур-ние П. и. выводит из ур-ний Максвелла
на основе волновых понятий, описывающих когерентные свойства излучения.
При таком подходе яркость I связана с Вигнера функцией распределения
Jk(R), а последняя - с функцией когерентности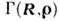 комплексной амплитуды поля. Для скалярного монохроматич. поля
комплексной амплитуды поля. Для скалярного монохроматич. поля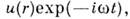 для к-рого
для к-рого
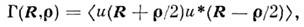
где (...) означает статистич. усреднение,
* - комплексное сопряжение,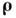 = r1 - r2 - разность, а R = (r1
+ r2)/2 - "центр тяжести" радиусов-векторов точек наблюдения
r1 и r2, функция Вигнера определяется как
= r1 - r2 - разность, а R = (r1
+ r2)/2 - "центр тяжести" радиусов-векторов точек наблюдения
r1 и r2, функция Вигнера определяется как
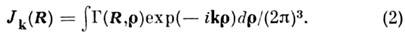
Для свободного статистически однородного
поля функция когерентности Г зависит только от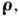 а функция Jk(R)связана с яркостью I соотношением
а функция Jk(R)связана с яркостью I соотношением
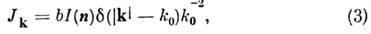
где k0 - волновое число,
b - коэф. пропорциональности, зависящий от выбора системы единиц.
Появление в (3) дельта-функции обусловлено волновым характером рассматриваемого
излучения: волновые векторы составляющих поле плоских волн локализованы
на поверхности |k| = k0, при этом, согласно Винера
- Хинчина теореме, I(n)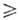 0.
0.
Соотношение (3) приближённо сохраняется
для квазиоднородного поля, ф-цпя когерентности к-рого плавно зависит от
R:
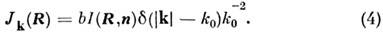
Условие квазиоднородности можно записать
в виде неравенства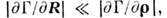 к-рое означает малость изменений функций когерентности по аргументу R в
сравнении с её изменениями по разностной переменной
к-рое означает малость изменений функций когерентности по аргументу R в
сравнении с её изменениями по разностной переменной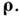 Классич. фотометрия соответствует некогерентному излучению, когда
Классич. фотометрия соответствует некогерентному излучению, когда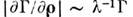 и
и
Входящую в (4) величину I(R,n)
считают обобщённой яркостью, зависящей от аргумента R. Согласно
(2, 4) величина I(R,n)пропорц. преобразованию Фурье от функции когерентности
Г по разностной переменной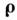 = r1 - r2, поэтому
= r1 - r2, поэтому
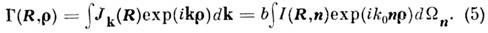
Значение соотношения (5) состоит в том, что оно связывает энергетнч. характеристику излучения (яркость I) с волновыми и статистич. характеристиками, а именно: с функцией когерентности волнового поля. Напр., для однородного и изотропного излучения яркость / не зависит от направления и, поэтому

Т, о., соотношение (5) позволяет переходить
от лучевого (энергетич.) описания к волновому (дифракционному) и тем самым
извлекать из ур-ния П. и. нек-рые сведения о дифракц. эффектах.
В общей теории многократного рассеяния
из ур-ния, определяющего поведение функции когерентности Г, следует, что
обобщённая яркость I(R,n)для достаточно разреженных рассеивающих
сред удовлетворяет ур-нию П. и. классич. теории (1).
Тем самым устанавливается строгий статистич.
смысл ур-ния П. и., одновременно находят выражения для входящих в (1) феноменологич.
коэф., к-рые в этом случае мало отличаются от результатов, полученных в
приближении однократного рассеяния. Такой подход позволяет использовать
хорошо развитый матем. аппарат теории П. и. для описания нек-рых дифракц.
и интерференц. эффектов, связанных с частичной когерентностью излучения.
В общем случае величина I(R,n) не обладает всеми свойствами феноменологич.
яркости, в частности, не является всюду неотрицательной.
Крупномасштабная среда. Статистико-волновое
содержание теории П. и. наглядно проявляется на примере крупномасштабной
статистически однородной рассеивающей среды. функция когерентности Г =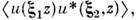
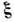 = (х,у), монохроматич. поля, распространяющегося в направлении оси z, удовлетворяет ур-нию
= (х,у), монохроматич. поля, распространяющегося в направлении оси z, удовлетворяет ур-нию
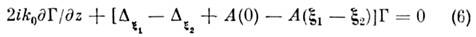
(см. Параболического уравнения приближение ).Величина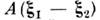 выражается через функцию корреляции флуктуации среды в точках
выражается через функцию корреляции флуктуации среды в точках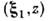 и
и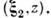 Отвечающая
этому случаю обобщённая яркость I определяется соотношением
Отвечающая
этому случаю обобщённая яркость I определяется соотношением
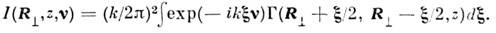
Здесь v - поперечная часть единичного
вектора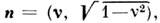 к-рая играет роль угл. переменной и описывает направленность излучения.
Яркость
к-рая играет роль угл. переменной и описывает направленность излучения.
Яркость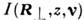 удовлетворяет вытекающему из (6) ур-нию П. и.:
удовлетворяет вытекающему из (6) ур-нию П. и.:
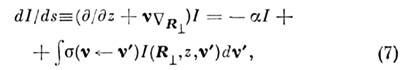
где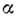 = А(0), а сечение рассеяния
= А(0), а сечение рассеяния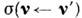 выражается через преобразование Фурье от
выражается через преобразование Фурье от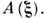 Поскольку ур-ние (7) эквивалентно ур-нию (6), оно учитывает все дифракц.
эффекты, описываемые волновым ур-нием (6).
Поскольку ур-ние (7) эквивалентно ур-нию (6), оно учитывает все дифракц.
эффекты, описываемые волновым ур-нием (6).
В ряде случаев решение ур-ния (7) можно
записать в явном виде. В простейшем случае свободного пространства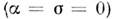 решение имеет вид
решение имеет вид
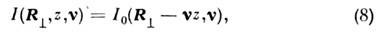
где I - обобщённая яркость при z
> 0, а I0 - распределение обобщённой яркости в нач. плоскости
z = 0. Это выражение отвечает сохранению величины I вдоль
"обобщённого" прямого луча, к-рый, в отличие от обычной геом. оптики, строится
для координаты R. В феноменологич. теории, использующей предельный
переход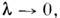 для исходной яркости I0 можно задавать произвольное угл.
распределение, ограниченное единств, условием I0
для исходной яркости I0 можно задавать произвольное угл.
распределение, ограниченное единств, условием I0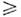 0.
В ф-ле (8) обобщённая яркость I связана преобразованием Фурье с
нач. функцией когерентности Г0 = Г|z=0, поэтому требование
I0
0.
В ф-ле (8) обобщённая яркость I связана преобразованием Фурье с
нач. функцией когерентности Г0 = Г|z=0, поэтому требование
I0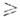 0 становится излишним. Эфф. угл. ширина
0 становится излишним. Эфф. угл. ширина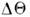 = |v| обобщённой яркости I [т. е. масштаб изменения
= |v| обобщённой яркости I [т. е. масштаб изменения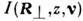 по аргументу v] подчиняется соотношению неопределённостей
по аргументу v] подчиняется соотношению неопределённостей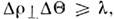 где
где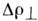 - эфф. ширина функции когерентности Г0 по аргументу
- эфф. ширина функции когерентности Г0 по аргументу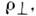 по порядку величины совпадающая с поперечным масштабом пространственной
когерентности пучка (в классич. фотометрии соотношение неопределённостей
не возникает из-за предельного перехода
по порядку величины совпадающая с поперечным масштабом пространственной
когерентности пучка (в классич. фотометрии соотношение неопределённостей
не возникает из-за предельного перехода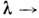 0). Продольный масштаб когерентности оценивается при помощи ф-лы (5), к-рая
в этом приближении принимает вид:
0). Продольный масштаб когерентности оценивается при помощи ф-лы (5), к-рая
в этом приближении принимает вид:
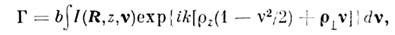
откуда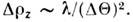
Оппсанный подход позволяет построить статистич.
теорию переноса частично когерентного излучения и даёт возможность обосновать
феноменологич. теорию для разреженных слабо рассеивающих сред. В противоположном
случае плотных и сильно рассеивающих сред существ. роль начинают играть
когерентные и кооперативные эффекты, при этом вопрос об области применимости
феноменологич. ур-ния П. и. остаётся до конца не выясненным. Для таких
сред фазовые соотношения между рассеянными волнами могут играть определяющую
роль. Кооперативные эффекты приводят, в частности, к фундаментальному для
теории аморфных тел явлению - андерсоновской локализации и, как
следствие, к качеств. изменению характера П. и. Напр., ур-ние П. и. не
в состоянии описать эффекты сильного рассеяния в одномерной модели рассеивающей
среды.
Ур-ние П. и. описывает и др. виды волнового
движения, при этом "яркость" I вводят при помощи соотношения (3)
с подходящим значением коэф. b, напр. в случае звукового поля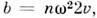 где п - плотность среды, v - скорость звука.
где п - плотность среды, v - скорость звука.
Лит.: Чандрасекар С., Перенос лучистой энергии, пер. с англ., М., 195Й; Сапожников Р. А., Теоретическая фотометрия, 3 изд., М., 1977; Рытов С. М., Кравцов Ю. А., Татарский В. И., Введение в статистическую радиофизику, ч. 2 - Случайные поля, М., 1978; Апресян Л. А., Кравцов Ю. А., Теория переноса излучения. Статистические и волновые аспекты, М., 1983.
Л. А. Апресян, Ю. А. Кравцов.
Перенос излучения в условиях немгновенности
элементарного акта рассеяния. Изложенный выше раздел теории П. и. относится
к области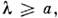 где
где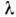 - длина
волны излучения, а - характерный масштаб макроскопич. флуктуации
в среде, на к-рых происходит рассеяние. В этом случае элементарный акт
рассеяния света единичным объёмом среды описывается в ур-нии (1) сечением
рассеяния
- длина
волны излучения, а - характерный масштаб макроскопич. флуктуации
в среде, на к-рых происходит рассеяние. В этом случае элементарный акт
рассеяния света единичным объёмом среды описывается в ур-нии (1) сечением
рассеяния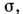 соответствующим данному типу флуктуации. Такой подход применим также и
к нерезонансному рассеянию света на микроскопич. флуктуациях распределения
частиц по координатам и импульсам. При этом а уже соответствует сечению
рассеяния света отдельной частицей (когерентному,
соответствующим данному типу флуктуации. Такой подход применим также и
к нерезонансному рассеянию света на микроскопич. флуктуациях распределения
частиц по координатам и импульсам. При этом а уже соответствует сечению
рассеяния света отдельной частицей (когерентному,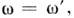 или некогерентному комбинационному рассеянию света атомом или молекулой,
комптоновскому рассеянию свободным электроном и др.). Общность формализма
описания П. и. в указанных случаях базируется на мгновенности процесса
рассеяния фотона средой (макроскопич. ансамблем или отдельной частицей),
что и позволяет свести описание П. и. к замкнутому ур-нию (1) для интенсивности.
или некогерентному комбинационному рассеянию света атомом или молекулой,
комптоновскому рассеянию свободным электроном и др.). Общность формализма
описания П. и. в указанных случаях базируется на мгновенности процесса
рассеяния фотона средой (макроскопич. ансамблем или отдельной частицей),
что и позволяет свести описание П. и. к замкнутому ур-нию (1) для интенсивности.
В теории П. и. важен более общий случай
немгновенного рассеяния света в элементарном акте, когда поглощение и рассеяние
следует рассматривать раздельно и происходит перераспределение излучения
по частоте. Эта область теории П. и. наиболее широко используется в астрофизике
[1,2]. Ур-ние для интен-сивности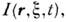 где
где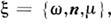 принимает вид:
принимает вид:
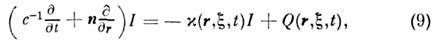
где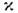 - вероятность поглощения фотона на единице длины пути, Q - объёмная
плотность мощности излучения среды, к-рая здесь учитывает также и упругое
рассеянпе света (функция источников), дифференциальная по всем параметрам
- вероятность поглощения фотона на единице длины пути, Q - объёмная
плотность мощности излучения среды, к-рая здесь учитывает также и упругое
рассеянпе света (функция источников), дифференциальная по всем параметрам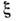 фотона
(
фотона
(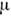 характеризует
поля-ризац. состояние фотона).
характеризует
поля-ризац. состояние фотона).
При отсутствии влияния элементарного акта
поглощения света на величину Q (т. е. Q не зависит от
I)
ур-ние (9) полностью описывает П. и. Это типично, напр., для П. и. электронами
плазмы путём тормозного, фоторекомбинац., циклотронного механизмов испускания
и поглощения (здесь Q не зависит от I при условии малости
влияния актов поглощения на функцию распределения электронов по импульсам,
как правило, равновесную). Если процессы релаксации к равновесию сильны
не только для электронов, но и для фотонов (распределение к-рых тогда близко
к распределению Планка с температурой электронов), то при условии малости эфф.
длины пробега фотонов по сравнению с характерным размером неоднородности
темн-ры ур-ние (9) сводится к простому ур-нию диффузионного типа для температуры
(лучистая теплопроводность, [3]). Перенос резонансного излучения. Др. важный
случай П. п. относится к резонансному рассеянию света на атомах или молекулах
среды. Поглощение резонансного фотона приводит к образованию возбуждённого
атома (ВА), к-рый подвергается сложному микроскопич. воздействию среды,
тогда как рассеяние нерезонансного фотона атомом соответствует виртуальному
(по сути мгновенному) возбуждению атома. В переносе резонансного излучения
функция источников Q определяется в общем случае функцией распределения
ВА по координатам, импульсам и параметрам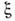 излучаемого в момент времени t фотона
излучаемого в момент времени t фотона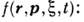
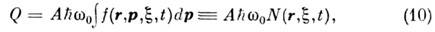
где А-1 - полное (интегральное
по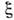 ) время
жизни ВА (для простоты двухуровневого) по отношению к радиац. распаду в
линии с частотой перехода
) время
жизни ВА (для простоты двухуровневого) по отношению к радиац. распаду в
линии с частотой перехода Коэф. поглощения
Коэф. поглощения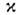 определяется сечением поглощения резонансного фотона невозбуждённым атомом
с импульсом р:
определяется сечением поглощения резонансного фотона невозбуждённым атомом
с импульсом р:
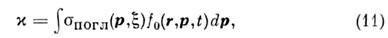
где f0 - функция распределения невозбуждённых атомов. функция распределения ВА является решением кинетич, уравнения
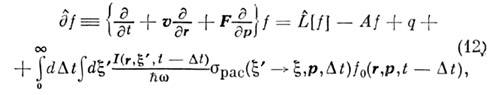
где F - внеш. сила, q - внеш. источник
ВА,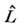 - оператор, описывающий все процессы взаимодействия ВА с окружающей средой
(включая процессы релаксации по р и
- оператор, описывающий все процессы взаимодействия ВА с окружающей средой
(включая процессы релаксации по р и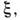 а также девозбуждение ВА столкновениями). Величина
а также девозбуждение ВА столкновениями). Величина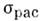 описывает дифференц. по
описывает дифференц. по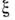 и
и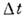 сечение двухступенчатого процесса поглощения отдельным атомом (с импульсом
р) фотона
сечение двухступенчатого процесса поглощения отдельным атомом (с импульсом
р) фотона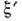 и
последующего переизлучения фотона
и
последующего переизлучения фотона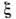 по прошествии времени
по прошествии времени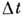 с учётом воздействия на ВА всех микро- и макроскопич. флуктуации среды.
Вероятность указанного процесса, интегральная по
с учётом воздействия на ВА всех микро- и макроскопич. флуктуации среды.
Вероятность указанного процесса, интегральная по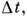 определяет широко используемую в астрофизике [1,2,4] функцию перераспределения
определяет широко используемую в астрофизике [1,2,4] функцию перераспределения фотона по его параметрам в акте рассеяния (как правило, по частоте, при
соответствующем усреднении по остальным параметрам). Свёртка функции R по
начальным или конечным параметрам фотона даёт соответственно контур линии
(т. е. плотность вероятности) испускания
фотона по его параметрам в акте рассеяния (как правило, по частоте, при
соответствующем усреднении по остальным параметрам). Свёртка функции R по
начальным или конечным параметрам фотона даёт соответственно контур линии
(т. е. плотность вероятности) испускания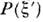 и поглощения
и поглощения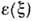 фотона:
фотона:
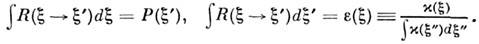
Фактически за перераспределение по частоте
отвечают те же механизмы, что и за уширение линии: допле-ровский, штарковский
и др.
Ур-ние (12) позволяет сформулировать критерий
мгновенности элементарного акта рассеяния: его эфф. длительность должна
быть мала по сравнению с характерными временами эволюции функции распределения
ВА под действием операторов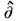 и
и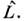 При выполнении этого условия ур-ние (9) с учётом ур-ний (10) и (12) переходит
в ур-ние (1).
При выполнении этого условия ур-ние (9) с учётом ур-ний (10) и (12) переходит
в ур-ние (1).
В том предельном случае, когда реализуется
полное "забывание" испущенным фотоном его состояния до поглощения, R расщепляется на произведение вероятностей поглощения и испусканий -
т. н. полное перераспределение по частоте (ППЧ). При этом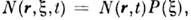 где N(r,t) - плотность ВА. Если можно пренебречь макроскопич. движением
среды за характерные времена эволюции излучения в данной среде, система
ур-ний (9 - 12) сводится к одному из основополагающих ур-ний теории П.
и. - ур-нию Бибермана - Холстейна (1947). В однородной стационарной среде
(объёма V)оно имеет вид
где N(r,t) - плотность ВА. Если можно пренебречь макроскопич. движением
среды за характерные времена эволюции излучения в данной среде, система
ур-ний (9 - 12) сводится к одному из основополагающих ур-ний теории П.
и. - ур-нию Бибермана - Холстейна (1947). В однородной стационарной среде
(объёма V)оно имеет вид

где vT - скорость нерадиационного
(прежде всего столкновительного) девозбуждения атома, а ядро G выражается
через вероятность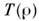 прохождения фотоном пути, не меньшего
прохождения фотоном пути, не меньшего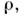 без поглощения:
без поглощения:
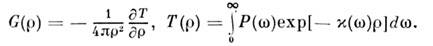
Выведенное первоначально из балансовых
соотношений ур-ние Бибермана - Холстейна было впоследствии обосновано в
рамках микроскопич. квантового описания эволюции фотонного газа в резонансной
атомной среде. Матем. аппарат теории П. и. в приближении ППЧ см. в [1,2,5].
ППЧ реализуется как при внеш. микроскопич.
воздействии [вследствие описываемого величинами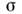 и
и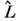 в (12) взаимодействия с др. частицами, приводящего к сбою фазы атомного
осциллятора - см. Уширение спектральных линий], так и в результате
хаотизации параметров излучаемого фотона независимо от микроскопич. воздействия
среды (при доплеровском уширении).
в (12) взаимодействия с др. частицами, приводящего к сбою фазы атомного
осциллятора - см. Уширение спектральных линий], так и в результате
хаотизации параметров излучаемого фотона независимо от микроскопич. воздействия
среды (при доплеровском уширении).
ППЧ соответствует случаю, когда наиб.
ярко выражено пленение излучения .В этом случае стационарное распределение
возбуждённых атомов в конечном объёме определяется вероятностью только
прямого, без рассеяния, выхода фотона из среды:
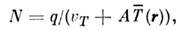
где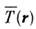 - усреднённая по углам вылета фотона вероятность выхода фотона, испущенного
в точке r, без рассеяния.
- усреднённая по углам вылета фотона вероятность выхода фотона, испущенного
в точке r, без рассеяния.
Совр. развитие теории переноса резонансного
излучения связано с выходом за рамки приближения ППЧ, т. к. практически
значим более общий случай - т. н. частичное перераспределение по частоте
[см. (12), [6]], имеющий место в астрофиз. объектах, в лабораторной плазме
с многозарядными ионами, для к-рых возрастание роли механизма спонтанного
испускания (A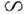 Z4,
Z - заряд иона) благоприятствует частичному сохранению памяти фотона
не только в далёком крыле линии.
Z4,
Z - заряд иона) благоприятствует частичному сохранению памяти фотона
не только в далёком крыле линии.

А. Б. Кукушкин, В. И. Коган
|
|