Маятник математический. Физический маятник. РЕАЛЬНАЯ ФИЗИКА. Глоссарий по физике

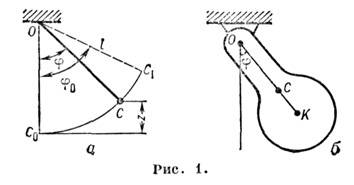
Маятник математический - упрощенная математическая модель гравитационного маятника, совершающего колебания под действием силы тяжести. Простейший маятник состоит из небольшого массивного груза С, подвешенного на нити (или лёгком стержне) длиной l. Если считать нить нерастяжимой и пренебречь размерами груза по сравнению с длиной нити, а массой нити по сравнению с массой груза, то груз на нити можно рассматривать как материальную точку, находящуюся на неизменном расстоянии l от точки подвеса О. (рис. 1, а).

Такой маятник называется круговым математическим маятником. Если, как это обычно имеет место, колеблющееся тело нельзя рассматривать как материальную точку, то маятник называется физическим (реальным).

Математический маятник (круговой)

Если маятник, отклонённый от равновесного положения C₀, отпустить без нач. скорости или сообщить точке С скорость, перпендикулярную ОС и лежащую в плоскости нач. отклонения, то маятник будет совершать колебания в одной вертнк. плоскости (плоский математический маятник). Если пренебречь трением в оси и сопротивлением воздуха (что в дальнейшем всегда предполагается), то для маятника будет иметь место закон сохранения механич. энергии, к-рый даёт:

где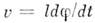

- скорость точки С,

-её координата, отсчитываемая вертикально вверх от равновесного положения, -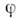

- угол отклонения M. от вертикали, g - ускорение силы тяжести, h - постоянная, пропорциональная полной механич. энергии M. и определяемая нач. значениями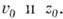

Когда сообщённая нач. энергия маятника такова, что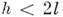

(для груза на стержне) или

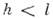(для груза на нити), то маятник будет совершать колебания с угл. амплитудой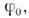

определяемой равенством

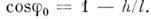Эти колебания не являются гармоническими; их период T зависит от амплитуды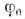и определяется след, ф-лой, получаемой из ур-ния (1):

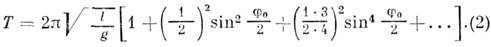
Когда указанные выше условия для k не выполняются, то M. не совершает колебат. движения. Напр., при

груз на стержне будет описывать окружность. Когда сообщённая M. нач. энергия очень мала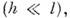

M. совершает малые колебания, близкие к гармоническим; период малых колебаний можно приближённо считать равным:

т. е. не зависящим от амплитуды (колебания изохронны). Ф-ла (3) по сравнению с (2) даёт погрешность до 0,05% при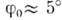

и до 1% при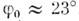

. Эти резуль-

таты справедливы для инерциальпой системы отсчёта. По отношению к Земле вследствие её суточного вращения плоскость качаний M. медленно изменяет своё направление (см. Фуко маятник).

Если отклонённому маятнику сообщить нач. скорость, не лежащую в плоскости нач. отклонения, то точка С будет описывать на сфере радиуса l кривые, заключённые между 2 параллелями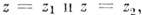

где значения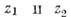

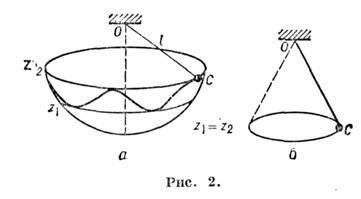
зависят от нач. условий (сферический маятник, рис. 2, я). В частном случае, при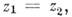

точка С будет описывать горизонтальную окружность (конический M., рис. 2, б). Из некруговых маятников особый интерес представляет циклоидальный маятник ,колебания к-рого изохронны при любой величине амплитуды.

Физический маятник

Физическим маятником обычно наз. твёрдое тело, совершающее под действием силы тяжести колебания вокруг горизонтальной оси подвеса (рис. 1, б). Движение такого M. вполне аналогично движению кругового матем. M. Период конечных или малых колебаний физ. M. определяется соответственно ф-лами (2) или (3), в к-рых l следует заменить величиной

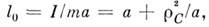где т - масса M., a - расстояние от центра тяжести С до оси подвеса, I - момент инерции M. относительно оси подвеса,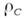

- радиус инерции относительно оси, параллельной оси подвеса и проходящей через С. Период зависит от положения оси подвеса относительно центра тяжести и будет наименьшим при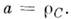

Величина l₀, к-рая всегда больше а, наз. приведённой длиной физ. M. Если отложить вдоль линии ОС отрезок OK = l₀, то полученная точка K паз. центром качаний физ. M. (матем. M. с массой, сосредоточенной в точке К, будет колебаться с тем же периодом, что и данный физ. M.). Точка оси подвеса О и центр качаний K обладают свойством взаимности: если M. подвесить так, чтобы ось подвеса прошла через K, то точка О станет центром качаний и период колебаний M. не изменится. На этом свойстве основано устройство оборотного M., применяемого для определения ускорения силы тяжести.

Свойствами M. широко пользуются в разл. приборах: часах, приборах для определения ускорения силы тяжести (маятниковый прибор), ускорений движущихся тел, колебаний земной коры (сейсмограф), в гироскопич. приборах, приборах для эксперим. определения моментов инерции тел и др.

Литература по маятникам

Знаете ли Вы, что, как и всякая идолопоклонническая религия, релятивизм ложен в своей основе. Он противоречит фактам. Среди них такие:

1. Электромагнитная волна (в религиозной терминологии релятивизма - "свет") имеет строго постоянную скорость 300 тыс.км/с, абсурдно не отсчитываемую ни от чего. Реально ЭМ-волны имеют разную скорость в веществе (например, ~200 тыс км/с в стекле и ~3 млн. км/с в поверхностных слоях металлов, разную скорость в эфире (см. статью "Температура эфира и красные смещения"), разную скорость для разных частот (см. статью "О скорости ЭМ-волн")

2. В релятивизме "свет" есть мифическое явление само по себе, а не физическая волна, являющаяся волнением определенной физической среды. Релятивистский "свет" - это волнение ничего в ничем. У него нет среды-носителя колебаний.

3. В релятивизме возможны манипуляции со временем (замедление), поэтому там нарушаются основополагающие для любой науки принцип причинности и принцип строгой логичности. В релятивизме при скорости света время останавливается (поэтому в нем абсурдно говорить о частоте фотона). В релятивизме возможны такие насилия над разумом, как утверждение о взаимном превышении возраста близнецов, движущихся с субсветовой скоростью, и прочие издевательства над логикой, присущие любой религии.

4. В гравитационном релятивизме (ОТО) вопреки наблюдаемым фактам утверждается об угловом отклонении ЭМ-волн в пустом пространстве под действием гравитации. Однако астрономам известно, что свет от затменных двойных звезд не подвержен такому отклонению, а те "подтверждающие теорию Эйнштейна факты", которые якобы наблюдались А. Эддингтоном в 1919 году в отношении Солнца, являются фальсификацией. Подробнее читайте в FAQ по эфирной физике.