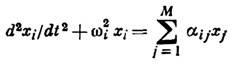
Линейное взаимодействие волн - явление перераспределения волнового движения между
различными нормальными волнами, происходящее в результате изменения свойств
среды в пространстве и(или) во времени под действием внеш. факторов. Это явление
наз. также линейной трансформацией волн. Оно не связано с нарушением принципа
суперпозиции волновых полей, в отличие от нелинейного взаимодействия волн, при
к-ром пространственно-временное изменение свойств среды обусловлено самими взаимодействующими
волнами.
Понятие "Линейное взаимодействие волн"
удобно рассмотреть на примере линейного взаимодействия колебаний. Напр., для
системы связанных осцилляторов
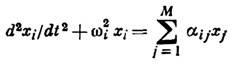
с изменяющимися на нек-ром
интервале времени  коэф. связи
коэф. связи 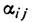 и частотами
и частотами 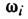 явление линейного взаимодействия 2М мод с собств. частотами
явление линейного взаимодействия 2М мод с собств. частотами 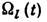 заключается в том, что амплитуды их колебаний, взаимно независимых при
заключается в том, что амплитуды их колебаний, взаимно независимых при 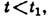 при
при 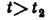 становятся
взаимно зависимыми. Взаимная трансформация мод
существенна, если характерное время изменения параметров системы меньше или
порядка периода биений
становятся
взаимно зависимыми. Взаимная трансформация мод
существенна, если характерное время изменения параметров системы меньше или
порядка периода биений 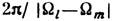 между к--л. двумя модами l и т. Если функции
между к--л. двумя модами l и т. Если функции 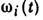 и
и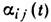 достаточно гладкие, то моды остаются независимыми; изменение их амплитуд (в
отсутствие диссипации энергии мод Wl) происходит в соответствии
с законом сохранения адиабатических инвариантов Ii=
достаточно гладкие, то моды остаются независимыми; изменение их амплитуд (в
отсутствие диссипации энергии мод Wl) происходит в соответствии
с законом сохранения адиабатических инвариантов Ii=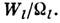 Поэтому говорят также о неадиа-батич. переходе между модами (см. также Пересечение
уровней). Линейное взаимодействие колебаний возникает при столкновении молекул,
в связанных радиотехн. контурах, СВЧ- или акустич. резонаторах и др. нестационарных
колебат. системах.
Поэтому говорят также о неадиа-батич. переходе между модами (см. также Пересечение
уровней). Линейное взаимодействие колебаний возникает при столкновении молекул,
в связанных радиотехн. контурах, СВЧ- или акустич. резонаторах и др. нестационарных
колебат. системах.
Аналогично, если свойства
стационарной сплошной среды или волновода меняются вдоль направления
распространения волн (ось z), то возникает линейное взаимодействие монохроматич.
нормальных волн с показателями преломления nl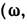 z) (и одинаковой частотой
z) (и одинаковой частотой 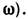 Исходная система ур-ний для вектора е, образованного TV комплексными
компонентами
Исходная система ур-ний для вектора е, образованного TV комплексными
компонентами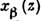 рассматриваемого волнового
поля, имеет вид
рассматриваемого волнового
поля, имеет вид 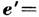 -iTe. Здесь опущен множитель ехр
-iTe. Здесь опущен множитель ехр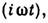 штрих обозначает дифференцирование по безразмерной координате
штрих обозначает дифференцирование по безразмерной координате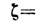 k0z,
где k0=
k0z,
где k0=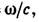 c=const
- характерная фазовая скорость волн. В каждой точке
c=const
- характерная фазовая скорость волн. В каждой точке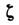 с
помощью ур-ния
с
помощью ур-ния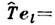 = н;// определяют полную систему собств. векторов е/ и их собств. значения
nl, l=1, . . ., N;
= н;// определяют полную систему собств. векторов е/ и их собств. значения
nl, l=1, . . ., N;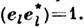
Замена е= где 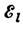 =Фlеl,
приводит к ур-ниям
=Фlеl,
приводит к ур-ниям
Л. в. в. 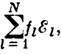
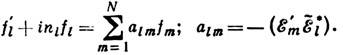
Здесь - означает комплексное сопряжение, а вид множителей Фl
- означает комплексное сопряжение, а вид множителей Фl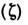 определён условием
определён условием 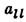 =0;
=0;
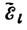 - взаимная
к
- взаимная
к 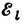 система
векторов.
система
векторов.
В приближении геом. оптики
alm=0 и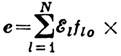
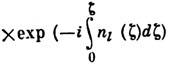 с постоянными fl0 (см. Геометрической оптики метод). Л. в. в. отвечает нарушению этого приближения, возникающему вследствие неоднородности
собств. векторов поляризации волн
с постоянными fl0 (см. Геометрической оптики метод). Л. в. в. отвечает нарушению этого приближения, возникающему вследствие неоднородности
собств. векторов поляризации волн 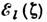 вдоль направления распространения, когда
вдоль направления распространения, когда  а значения flо нельзя считать постоянными, ь прозрачной среде
при
а значения flо нельзя считать постоянными, ь прозрачной среде
при 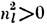 Л. в. в. характеризуется перераспределением их потоков энергии, равных
Л. в. в. характеризуется перераспределением их потоков энергии, равных 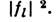 Возможна взаимная трансформация как встречных волн (прямой и отражённой), так
и попутных волн (распространяющихся в одном направлении). Как и в случае нестационарных
связанных колебаний, Л. в. в. несущественно, если характерный масштаб изменения
функций
Возможна взаимная трансформация как встречных волн (прямой и отражённой), так
и попутных волн (распространяющихся в одном направлении). Как и в случае нестационарных
связанных колебаний, Л. в. в. несущественно, если характерный масштаб изменения
функций 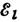
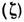 велик
по сравнению с пространственным периодом биений волн
велик
по сравнению с пространственным периодом биений волн 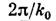 \nl-nm\. Поэтому в плавно неоднородной среде Л. в. в. происходит только в области
сближения показателей преломления nl и пт (для
попутных волн) либо в области малых значений показателей преломления (для встречных
волн). В слабо неоднородной среде эффективное Л. в. в. возможно при наличии
периодич. модуляции её свойств вдоль направления распространения. Оно возникает
вследствие пространственного параметрического резонанса к--л. двух волн
при условии, что период модуляции примерно кратен периоду биений между ними.
Это отвечает Брэгга - Вулъфа условию в случае трансформации двух встречных
волн одного типа, когда пт= -ni.
\nl-nm\. Поэтому в плавно неоднородной среде Л. в. в. происходит только в области
сближения показателей преломления nl и пт (для
попутных волн) либо в области малых значений показателей преломления (для встречных
волн). В слабо неоднородной среде эффективное Л. в. в. возможно при наличии
периодич. модуляции её свойств вдоль направления распространения. Оно возникает
вследствие пространственного параметрического резонанса к--л. двух волн
при условии, что период модуляции примерно кратен периоду биений между ними.
Это отвечает Брэгга - Вулъфа условию в случае трансформации двух встречных
волн одного типа, когда пт= -ni.
Линейное взаимодействие волн определяет спектр
и поляризацию отраженного и проходящего излучения. Поэтому измерение параметров
излучения позволяет судить о локальной неоднородности среды в области Л. в.
в., а изменение неоднородности позволяет управлять свойствами излучения. Эти
возможности используют, напр., в физике плазмы (лабораторной и космической),
физике лазеров, акустоэлектронике и акустооптике, оптике жидких кристаллов,
магнитооптике, волоконной оптике, в волноводах и др. линиях передачи.
При распространении через неоднородный слой нестационарной среды возможно
линейное взаимодействие волн на разных частотах.
В частном случае слабого периодич. возмущения свойств среды наиб. благоприятные
условия линейного взаимодействия волн отвечают параметрич. взаимодействию тех волн, для к-рых невозмущённые
частоты  2
и волновые векторы k1, 2 связаны с частотой
2
и волновые векторы k1, 2 связаны с частотой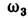 и волновым вектором k3 возмущений в слое условиями
волнового синхронизма:
и волновым вектором k3 возмущений в слое условиями
волнового синхронизма: 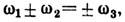 k1bk2=bk3. Если дисперсия
волн отсутствует, то линейное взаимодействие волн в пространстве сводится к линейному взаимодействию
колебаний (в системе отсчёта, движущейся вместе с неоднородностями среды).
k1bk2=bk3. Если дисперсия
волн отсутствует, то линейное взаимодействие волн в пространстве сводится к линейному взаимодействию
колебаний (в системе отсчёта, движущейся вместе с неоднородностями среды).

В. В. Кочаровский, Вл. В. Кочаровский
|
|