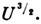 .
.
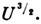 .
.
Для частного случая бесконечно протяжённых плоских электродов такую зависимость впервые (1911) получил К. Д. Чайлд (С. D. Child) при упрощающем предположении, что начальные скорости электронов равны нулю:
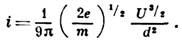
Здесь d - расстояние между электродами, е и т - заряд и масса электронов.
Однако своё название формула Ленгмюра получила по имени И. Ленгмюра
(I. Langmuir), исследовавшего эту зависимость
для др. конфигураций электродов (1913). Для коаксиальных цилиндрич. электродов,
из к-рых эмитирует электроны внутренний, Л. ф. имеет вид

Здесь 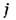 -
ток на единицу длины цилиндров,
-
ток на единицу длины цилиндров, 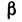 -
табулиров. функция отношения радиусов внешнего r и внутреннего r0
цилиндров.
-
табулиров. функция отношения радиусов внешнего r и внутреннего r0
цилиндров.
Для концентрич. сфер с радиусами r (внешняя) и r0 (внутренняя) Л. ф. принимает вид
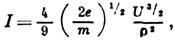
где 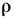 - табулиров. функция отношений
- табулиров. функция отношений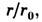 а I - полный ток на сферу. В связи с общей для всех выражений Л. ф. зависимостью
тока (или плотности тока) от разности потенциалов между электродами Л. ф. часто
наз. "законом трёх вторых".
а I - полный ток на сферу. В связи с общей для всех выражений Л. ф. зависимостью
тока (или плотности тока) от разности потенциалов между электродами Л. ф. часто
наз. "законом трёх вторых".
Учёт начальных скоростей электронов эмиссии объясняет образование между катодом и анодом минимума потенциала (см. Виртуальный катод ). Формула Ленгмюра играет важную роль при расчёте и конструировании вакуумных электронных приборов (прежде всего, ламп с накалённым катодом).

Л. А. Сена
1. Электромагнитная волна (в религиозной терминологии релятивизма - "свет") имеет строго постоянную скорость 300 тыс.км/с, абсурдно не отсчитываемую ни от чего. Реально ЭМ-волны имеют разную скорость в веществе (например, ~200 тыс км/с в стекле и ~3 млн. км/с в поверхностных слоях металлов, разную скорость в эфире (см. статью "Температура эфира и красные смещения"), разную скорость для разных частот (см. статью "О скорости ЭМ-волн")
2. В релятивизме "свет" есть мифическое явление само по себе, а не физическая волна, являющаяся волнением определенной физической среды. Релятивистский "свет" - это волнение ничего в ничем. У него нет среды-носителя колебаний.
3. В релятивизме возможны манипуляции со временем (замедление), поэтому там нарушаются основополагающие для любой науки принцип причинности и принцип строгой логичности. В релятивизме при скорости света время останавливается (поэтому в нем абсурдно говорить о частоте фотона). В релятивизме возможны такие насилия над разумом, как утверждение о взаимном превышении возраста близнецов, движущихся с субсветовой скоростью, и прочие издевательства над логикой, присущие любой религии.
4. В гравитационном релятивизме (ОТО) вопреки наблюдаемым фактам утверждается об угловом отклонении ЭМ-волн в пустом пространстве под действием гравитации. Однако астрономам известно, что свет от затменных двойных звезд не подвержен такому отклонению, а те "подтверждающие теорию Эйнштейна факты", которые якобы наблюдались А. Эддингтоном в 1919 году в отношении Солнца, являются фальсификацией. Подробнее читайте в FAQ по эфирной физике.
|
|