Колебательно-вращательное взаимодействие молекул. РЕАЛЬНАЯ ФИЗИКА. Глоссарий по физике

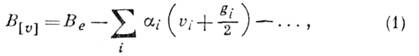
Вращат. и колебат. движения в молекуле не являются независимыми. При колебаниях молекулы изменяются её моменты инерции. Поэтому вращат. уровни энергии колеблющейся молекулы отличаются от соответствующих уровней "жёсткой" молекулы - молекулы с неподвижными атомными ядрами. Если считать, что вращат. постоянные А, В, С и центробежная постоянная D зависят от колебат. состояния, то, напр., для вращат. постоянной В получим:

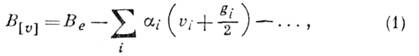
где В_е - вращат. постоянная в равновесной конфигурации,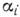

- малые по сравнению с В_е величины, g,- - кратность вырождения нормального колебания Q_i, суммирование проводится по всем г нормальным колебаниям. Аналогично получаются выражения для др. вращат. постоянных, к-рые позволяют вычислить вращат. уровни энергии двухатомных и многоатомных молекул в невырожденном колебат. состоянии с очень высокой точностью. В вырожденном колебат. состоянии К--в. в. приводит к более сильным эффектам, чем приведённое изменение вращат. постоянных (1). Это связано с наличием колебат. момента импульса в вырожденном колебат. состоянии.

В случае линейной многоатомной молекулы колебат. момент может принимать значения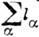

, где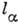

,...,-

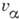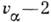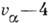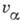, а суммирование проводится по всем вырожденным колебаниям. В сумме с электронным моментом он даёт полный момент молекулы l относительно её оси. Поскольку полный момент J не может быть меньше момента относительно оси, то l пробегает значения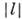

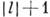, . . . Состояний с J=0, 1, . . .,

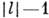не существует.

При возбуждении дважды вырожденных колебаний молекул типа симметричного волчка и трижды вырожденных колебаний молекул типа сферич. волчка наиб. сильным становится кориолисово К--в. в. Оно приводит к появлению члена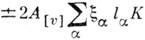

в выражении для вращат. энергии симметричного волчка, где А вращат. постоянная, 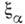- кориолисова постоянная

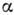-го колебания,

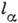- колебат. момент, К - проекция момента молекулы на ось волчка. Этот член снимает вырождение по знаку К. Для сферич. волчка в состоянии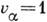

трижды вырожденного нормального колебания кориолисово взаимодействие вызывает расщепление вращат. уровня на три подуровня с энергиями:

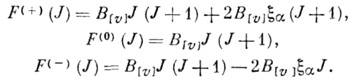
Кориолисовы постоянные всегда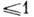

и имеют порядок 10^-1-10^-2. См. также ст. Молекула.

Литература по колебательно-вращательному взаимодействию молекул

Знаете ли Вы, что такое мысленный эксперимент, gedanken experiment?
Это несуществующая практика, потусторонний опыт, воображение того, чего нет на самом деле. Мысленные эксперименты подобны снам наяву. Они рождают чудовищ. В отличие от физического эксперимента, который является опытной проверкой гипотез, "мысленный эксперимент" фокуснически подменяет экспериментальную проверку желаемыми, не проверенными на практике выводами, манипулируя логикообразными построениями, реально нарушающими саму логику путем использования недоказанных посылок в качестве доказанных, то есть путем подмены. Таким образом, основной задачей заявителей "мысленных экспериментов" является обман слушателя или читателя путем замены настоящего физического эксперимента его "куклой" - фиктивными рассуждениями под честное слово без самой физической проверки.
Заполнение физики воображаемыми, "мысленными экспериментами" привело к возникновению абсурдной сюрреалистической, спутанно-запутанной картины мира. Настоящий исследователь должен отличать такие "фантики" от настоящих ценностей.

Релятивисты и позитивисты утверждают, что "мысленный эксперимент" весьма полезный интрумент для проверки теорий (также возникающих в нашем уме) на непротиворечивость. В этом они обманывают людей, так как любая проверка может осуществляться только независимым от объекта проверки источником. Сам заявитель гипотезы не может быть проверкой своего же заявления, так как причина самого этого заявления есть отсутствие видимых для заявителя противоречий в заявлении.

Это мы видим на примере СТО и ОТО, превратившихся в своеобразный вид религии, управляющей наукой и общественным мнением. Никакое количество фактов, противоречащих им, не может преодолеть формулу Эйнштейна: "Если факт не соответствует теории - измените факт" (В другом варианте " - Факт не соответствует теории? - Тем хуже для факта").

Максимально, на что может претендовать "мысленный эксперимент" - это только на внутреннюю непротиворечивость гипотезы в рамках собственной, часто отнюдь не истинной логики заявителя. Соответсвие практике это не проверяет. Настоящая проверка может состояться только в действительном физическом эксперименте.

Эксперимент на то и эксперимент, что он есть не изощрение мысли, а проверка мысли. Непротиворечивая внутри себя мысль не может сама себя проверить. Это доказано Куртом Гёделем.

Понятие "мысленный эксперимент" придумано специально спекулянтами - релятивистами для шулерской подмены реальной проверки мысли на практике (эксперимента) своим "честным словом". Подробнее читайте в FAQ по эфирной физике.