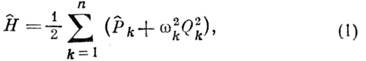
Колебания молекул - один из осн. видов внутримолекулярного движения, при к-ром происходит периодич.
изменение относит, расположения ядер атомов, составляющих молекулу. Роль потенц.
энергии для ядерного движения играет адиабатич. электронная энергия как функция
ядерных координат: U(r1 . . ., rN). В
общем случае нелинейных молекул адиабатич. электронная энергия зависит от 3N-6
относит. координат ядер (N - число атомов в молекуле). Образование устойчивой
молекулы возможно лишь при условии, что при нек-рых конечных значениях координат
ядер ri, i=l, . . ., N, функция U имеет
мин. значение. Координаты ri соответствуют равновесному
расположению ядер, т. е. характеризуют равновесную конфигурацию молекулы.
При малых отклонениях от
положений равновесия ядра будут совершать малые колебания. В случае N-атомной
нелинейной молекулы, ядра к-рой в равновесной конфигурации не лежат на одной
прямой, ко-лебат. движение характеризуется n=3N-6 степенями свободы.
В случае линейных молекул колебат. движение имеет n=3N-5 степеней свободы.
Гамильтониан системы, совершающей малые колебания около положений равновесия,
в гармонич. приближении может быть записан в виде
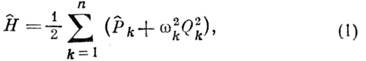
где Qk - нормальные координаты, или моды, колебаний, число к-рых равно числу колебат.
степеней свободы молекулы,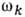 
- частоты соответствующих им независимых колебаний, 
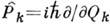- операторы импульсов, соответствующих нормальным колебаниям Qk. Поскольку гамильтониан (1) распадается на сумму независимых слагаемых, то
колебат. уровни энергии представляются суммами:
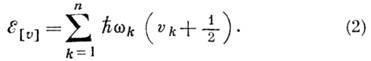
Волновые функции можно представить
в виде произведений соответствующих функций гармонич. осцилляторов:
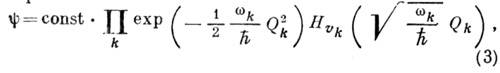
где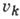 
- колебат. квантовое число, - полином
Эрмита степени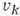 
(см. Ортогональные 
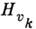полиномы).
Энергия самого низкого
уровня энергии, для к-рого
все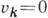 
,
равна и наз. энергией нулевых
колебаний. Уровни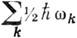
энергии, для к-рых все 
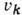равны нулю за исключением одного, равного 1, наз. фундаментальными. Уровни энергии
с одним
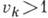наз. обертонными. Составные, или комбинационные, уровни энергии характеризуются
неск. отличными от нуля квантовыми числами
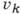. Схема колебат. уровней энергии приведена на рис. 1.
Если неск. нормальным колебаниям
соответствует одна и та же частота wk, то её наз. кратной
частотой. При наличии кратных частот в выражении для уровней энергии (2) появляются
члены вида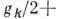
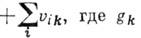- число нормальных колебаний, имеющих частоту 
,
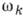т. е. кратность частоты. В этом случае положение колебат. уровней энергии молекулы
определяется квантовым числом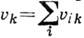 
и может иметь
одно и то же значение для
разл. наборов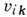 
,
т. е. уровень энергии вырождается. При этом кратность вырождения равна
Рис. 1. Общая схема расположения
колебательных уровней энергии многоатомной молекулы.
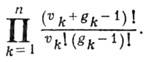
Т. о., основной уровень
энергии невырожден, кратность вырождения фундаментального уровня равна кратности
частоты.
Появление кратных частот
в К. м. связано с симметрией их равновесной конфигурации. Гамильтониан молекулы
(1) должен быть инвариантным относительно
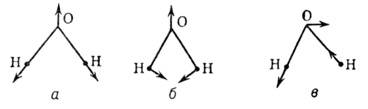
Рис. 2. Нормальные колебания
молекулы воды: а - симметричное валентное колебание; б - деформационное колебание:
в - антисимметричное валентное колебание.
преобразований симметрии.
Это значит, что нормальные координаты, соответствующие одной и той же кратной
частоте, осуществляют неприводимое представление группы симметрии молекулы;
размерность этого представления равна кратности частоты. Для молекул с низкой
симметрией возможны только невырожденные колебания, для молекул более высокой
симметрии наряду с невырожденными возможны и дважды и трижды вырожденные колебания.
К. м. можно разделить на
валентные, при к-рых изменяются в основном длины связей, и деформационные, при
к-рых .изменяются углы связей. Напр., молекула Н2О (группа симметрии
С2V)имеет два валентных колебания и одно деформационное (рис.
2). Молекула СO2 (группа симметрии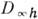 
)
имеет два невырожденных валентных колебания и одно дважды вырожденное деформационное
колебание (рис. 3).
При учёте членов 3-го и
4-го порядков в разложении потенц. энергии по степеням нормальных координат
появляются ангармонич. поправки к уровням энергии гармонич. приближения. В случае
двухатомной молекулы уровни колебат. энергии с учётом ангармонизма даются ф-лой
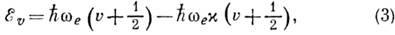
где индекс е означает
гармонич. приближение, а постоянная ангармоничности 
,
как правило, не превышает 0,01-0,02. Наиб. значение она имеет для молекулы водорода
(0,0285) и нек-рых гидридов.
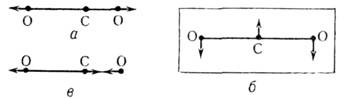
Рис. 3. Нормальные колебания
молекулы СО2: а - симметричное валентное колебание; б - дважды вырожденное деформационное колебание; в - антисимметричное валентное
колебание.
Для многоатомных молекул
уровни колебат. энергии с учётом ангармонизма в общем случае даются ф-лой
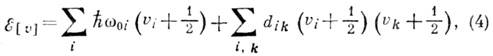
где индексом 0 выделены
частоты гармонич. приближения. Ангармонич. поправка (второй член) содержит слагаемые
вида 
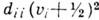, характеризующие
внут-римодовый ангармонизм, и слагаемые вида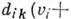
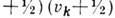с 
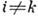, характеризующие
межмодовый ангармонизм (dik - постоянные ангармоничности).
Вследствие межмодового ангармонизма нормальные колебания молекулы перестают
быть взаимно независимыми. Это особенно сильно проявляется при наличии т. н.
резонансов Ферми. Если двум колебат. состояниям в гармонич. приближении соответствуют
одинаковые или почти одинаковые энергии, а ангармонич. члены в разложении потенц.
энергии имеют ненулевые матричные элементы между этими состояниями, то возникает
сильное взаимодействие между этими уровнями (резонанс). Резонанс Ферми приводит
к значит, изменениям соответствующих уровней энергии и форм колебаний по сравнению
с гармопич. приближением, а следовательно, и частот и интенсивностей в спектрах
колебат. переходов (см. Молекулярные спектры В ).сложных многоатомных
молекулах резонансы Ферми весьма вероятны даже при невысоком уровне возбуждения
и потому необходимо считаться с ним при интерпретации колебательных спектров.
Для определ. связей и валентных углов в молекулах и для разл. их сочетаний характерны определённые частоты колебаний - т. н. характеристические частоты.
Курдоглян.
|
|
 |
