Квадрупольное взаимодействие - взаимодействие системы с внеш. полем (или создающими его источниками), обусловленное наличием у системы квадрупольного момента. К. в. вызывается неоднородностью внеш. поля, к-рая обычно предполагается малой на размере системы l (т. е. поле мало изменяется в пределах системы). Так, энергия системы электрич. зарядов, напр, молекулы или атомного ядра, в электрич. поле E(r)=-Сj0(r), описываемом плавной гармонич. функцией j0(r) (Dj0=0) равна
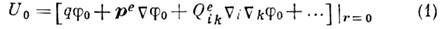
(здесь и далее по повторяющимся индексам i и k производится суммирование).
В (1) учтены только первые три электрич. мультипольных момента - полный заряд q, дипольный момент ре и квадрупольный момент 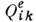 (i, А=1, 2, 3), вычисленные относительно к--л. внутр. точки системы
r=0. К. в. отвечает последнее слагаемое в ф-ле (1). Оно описывает
изменение энергии системы под действием неоднородности поля E(r), к-рую
т. о. неявно характеризует. Это обстоятельство используется, в
частности, в спектроскопии ядерного квадрупольного резонанса,
позволяющей получать информацию об электронной структуре молекулы путём
измерения квадрупольного расщепления энергетич. уровней её резонансных
ядер в неоднородном поле окружающих электронов.
Если внеш. поле создано нек-рой удалённой системой зарядов,
расположенной в области с размером l0 в окрестности точки R(Rдl, l0)и обладающей, в свою очередь, мультиполышми моментами q0,
(i, А=1, 2, 3), вычисленные относительно к--л. внутр. точки системы
r=0. К. в. отвечает последнее слагаемое в ф-ле (1). Оно описывает
изменение энергии системы под действием неоднородности поля E(r), к-рую
т. о. неявно характеризует. Это обстоятельство используется, в
частности, в спектроскопии ядерного квадрупольного резонанса,
позволяющей получать информацию об электронной структуре молекулы путём
измерения квадрупольного расщепления энергетич. уровней её резонансных
ядер в неоднородном поле окружающих электронов.
Если внеш. поле создано нек-рой удалённой системой зарядов,
расположенной в области с размером l0 в окрестности точки R(Rдl, l0)и обладающей, в свою очередь, мультиполышми моментами q0, 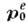 ,
, 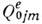 ,..., то его потенциал (в Гаусса системе единиц) равен
,..., то его потенциал (в Гаусса системе единиц) равен
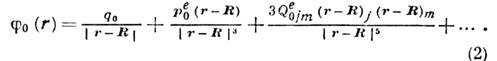
Подстановка (2) в (1) приводит к след. асимптотич. разложению энергии К. в. 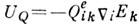 одной системы зарядов в эл--статич. поле другой:
одной системы зарядов в эл--статич. поле другой:
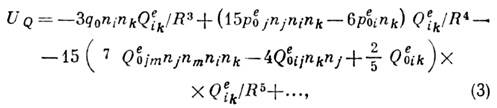
где 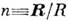 . Здесь первый член описывает энергию взаимодействия квадруполя с зарядом q0, второй - с диполем
. Здесь первый член описывает энергию взаимодействия квадруполя с зарядом q0, второй - с диполем 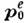 , третий - с квадруполем
, третий - с квадруполем 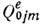 .
К. в. с зарядом
реализуется, напр., при кулоновском возбуждении несферич. ядер на
вращат. уровень энергии в процессе рассеяния заряж. частиц ядрами.
Собственно квадруполь-квадрупольное взаимодействие с энергией
.
К. в. с зарядом
реализуется, напр., при кулоновском возбуждении несферич. ядер на
вращат. уровень энергии в процессе рассеяния заряж. частиц ядрами.
Собственно квадруполь-квадрупольное взаимодействие с энергией 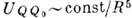 наиб. важно для незаряж. систем с нулевыми дипольными моментами. Такая
ситуация имеет место, в частности, при взаимодействии между состоящими
из одинаковых атомов двухатомными молекулами в основном состоянии или
между атомами с ненулевыми орбитальным (L№0) и полным (I№0, 1/2)угл.
моментами. Однако при усреднении по всевозможным ориентациям моментов
молекул или атомов, напр., в газе, соответствующая сила притяжения (либо
отталкивания)
наиб. важно для незаряж. систем с нулевыми дипольными моментами. Такая
ситуация имеет место, в частности, при взаимодействии между состоящими
из одинаковых атомов двухатомными молекулами в основном состоянии или
между атомами с ненулевыми орбитальным (L№0) и полным (I№0, 1/2)угл.
моментами. Однако при усреднении по всевозможным ориентациям моментов
молекул или атомов, напр., в газе, соответствующая сила притяжения (либо
отталкивания) 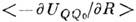 обращается в нуль. Последнее справедливо также по отношению к любым
силам, обусловленным собственными дипольными или высшими мультипольными
моментами частиц. Поэтому, согласно квантовомеханич. расчётам,
усреднённые силы между молекулами (или атомами) в газе на больших
расстояниях обычно определяются не эл--статич., а высокочастотной
эл--магн. энергией наведённого диполь-дипольного взаимодействия U~-1/R6, возникающего вследствие деформации одной молекулой электронного облака другой (см. Межмолекулярное взаимодействие).
обращается в нуль. Последнее справедливо также по отношению к любым
силам, обусловленным собственными дипольными или высшими мультипольными
моментами частиц. Поэтому, согласно квантовомеханич. расчётам,
усреднённые силы между молекулами (или атомами) в газе на больших
расстояниях обычно определяются не эл--статич., а высокочастотной
эл--магн. энергией наведённого диполь-дипольного взаимодействия U~-1/R6, возникающего вследствие деформации одной молекулой электронного облака другой (см. Межмолекулярное взаимодействие).
Знаете ли Вы, в чем ложность понятия "физический вакуум"?
Физический вакуум - понятие релятивистской квантовой физики, под ним там понимают низшее (основное) энергетическое состояние квантованного поля, обладающее нулевыми импульсом, моментом импульса и другими квантовыми числами. Физическим вакуумом релятивистские теоретики называют полностью лишённое вещества пространство, заполненное неизмеряемым, а значит, лишь воображаемым полем. Такое состояние по мнению релятивистов не является абсолютной пустотой, но пространством, заполненным некими фантомными (виртуальными) частицами. Релятивистская квантовая теория поля утверждает, что, в согласии с принципом неопределённости Гейзенберга, в физическом вакууме постоянно рождаются и исчезают виртуальные, то есть кажущиеся (кому кажущиеся?), частицы: происходят так называемые нулевые колебания полей. Виртуальные частицы физического вакуума, а следовательно, он сам, по определению не имеют системы отсчета, так как в противном случае нарушался бы принцип относительности Эйнштейна, на котором основывается теория относительности (то есть стала бы возможной абсолютная система измерения с отсчетом от частиц физического вакуума, что в свою очередь однозначно опровергло бы принцип относительности, на котором постороена СТО). Таким образом, физический вакуум и его частицы не есть элементы физического мира, но лишь элементы теории относительности, которые существуют не в реальном мире, но лишь в релятивистских формулах, нарушая при этом принцип причинности (возникают и исчезают беспричинно), принцип объективности (виртуальные частицы можно считать в зависимсоти от желания теоретика либо существующими, либо не существующими), принцип фактической измеримости (не наблюдаемы, не имеют своей ИСО).
Когда тот или иной физик использует понятие "физический вакуум", он либо не понимает абсурдности этого термина, либо лукавит, являясь скрытым или явным приверженцем релятивистской идеологии.
Понять абсурдность этого понятия легче всего обратившись к истокам его возникновения. Рождено оно было Полем Дираком в 1930-х, когда стало ясно, что отрицание эфира в чистом виде, как это делал великий математик, но посредственный физик Анри Пуанкаре, уже нельзя. Слишком много фактов противоречит этому.
Для защиты релятивизма Поль Дирак ввел афизическое и алогичное понятие отрицательной энергии, а затем и существование "моря" двух компенсирующих друг друга энергий в вакууме - положительной и отрицательной, а также "моря" компенсирующих друг друга частиц - виртуальных (то есть кажущихся) электронов и позитронов в вакууме.
Однако такая постановка является внутренне противоречивой (виртуальные частицы ненаблюдаемы и их по произволу можно считать в одном случае отсутствующими, а в другом - присутствующими) и противоречащей релятивизму (то есть отрицанию эфира, так как при наличии таких частиц в вакууме релятивизм уже просто невозможен). Подробнее читайте в FAQ по эфирной физике.
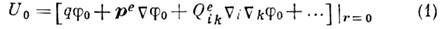
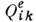 (i, А=1, 2, 3), вычисленные относительно к--л. внутр. точки системы
r=0. К. в. отвечает последнее слагаемое в ф-ле (1). Оно описывает
изменение энергии системы под действием неоднородности поля E(r), к-рую
т. о. неявно характеризует. Это обстоятельство используется, в
частности, в спектроскопии ядерного квадрупольного резонанса,
позволяющей получать информацию об электронной структуре молекулы путём
измерения квадрупольного расщепления энергетич. уровней её резонансных
ядер в неоднородном поле окружающих электронов.
Если внеш. поле создано нек-рой удалённой системой зарядов,
расположенной в области с размером l0 в окрестности точки R(Rдl, l0)и обладающей, в свою очередь, мультиполышми моментами q0,
(i, А=1, 2, 3), вычисленные относительно к--л. внутр. точки системы
r=0. К. в. отвечает последнее слагаемое в ф-ле (1). Оно описывает
изменение энергии системы под действием неоднородности поля E(r), к-рую
т. о. неявно характеризует. Это обстоятельство используется, в
частности, в спектроскопии ядерного квадрупольного резонанса,
позволяющей получать информацию об электронной структуре молекулы путём
измерения квадрупольного расщепления энергетич. уровней её резонансных
ядер в неоднородном поле окружающих электронов.
Если внеш. поле создано нек-рой удалённой системой зарядов,
расположенной в области с размером l0 в окрестности точки R(Rдl, l0)и обладающей, в свою очередь, мультиполышми моментами q0, 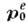 ,
, 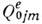 ,..., то его потенциал (в Гаусса системе единиц) равен
,..., то его потенциал (в Гаусса системе единиц) равен
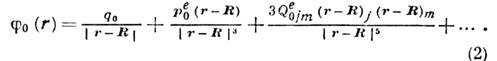
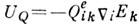 одной системы зарядов в эл--статич. поле другой:
одной системы зарядов в эл--статич. поле другой:
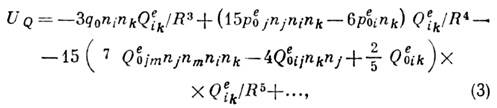
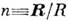 . Здесь первый член описывает энергию взаимодействия квадруполя с зарядом q0, второй - с диполем
. Здесь первый член описывает энергию взаимодействия квадруполя с зарядом q0, второй - с диполем 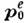 , третий - с квадруполем
, третий - с квадруполем 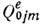 .
К. в. с зарядом
реализуется, напр., при кулоновском возбуждении несферич. ядер на
вращат. уровень энергии в процессе рассеяния заряж. частиц ядрами.
Собственно квадруполь-квадрупольное взаимодействие с энергией
.
К. в. с зарядом
реализуется, напр., при кулоновском возбуждении несферич. ядер на
вращат. уровень энергии в процессе рассеяния заряж. частиц ядрами.
Собственно квадруполь-квадрупольное взаимодействие с энергией 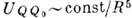 наиб. важно для незаряж. систем с нулевыми дипольными моментами. Такая
ситуация имеет место, в частности, при взаимодействии между состоящими
из одинаковых атомов двухатомными молекулами в основном состоянии или
между атомами с ненулевыми орбитальным (L№0) и полным (I№0, 1/2)угл.
моментами. Однако при усреднении по всевозможным ориентациям моментов
молекул или атомов, напр., в газе, соответствующая сила притяжения (либо
отталкивания)
наиб. важно для незаряж. систем с нулевыми дипольными моментами. Такая
ситуация имеет место, в частности, при взаимодействии между состоящими
из одинаковых атомов двухатомными молекулами в основном состоянии или
между атомами с ненулевыми орбитальным (L№0) и полным (I№0, 1/2)угл.
моментами. Однако при усреднении по всевозможным ориентациям моментов
молекул или атомов, напр., в газе, соответствующая сила притяжения (либо
отталкивания) 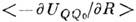 обращается в нуль. Последнее справедливо также по отношению к любым
силам, обусловленным собственными дипольными или высшими мультипольными
моментами частиц. Поэтому, согласно квантовомеханич. расчётам,
усреднённые силы между молекулами (или атомами) в газе на больших
расстояниях обычно определяются не эл--статич., а высокочастотной
эл--магн. энергией наведённого диполь-дипольного взаимодействия U~-1/R6, возникающего вследствие деформации одной молекулой электронного облака другой (см. Межмолекулярное взаимодействие).
обращается в нуль. Последнее справедливо также по отношению к любым
силам, обусловленным собственными дипольными или высшими мультипольными
моментами частиц. Поэтому, согласно квантовомеханич. расчётам,
усреднённые силы между молекулами (или атомами) в газе на больших
расстояниях обычно определяются не эл--статич., а высокочастотной
эл--магн. энергией наведённого диполь-дипольного взаимодействия U~-1/R6, возникающего вследствие деформации одной молекулой электронного облака другой (см. Межмолекулярное взаимодействие).
