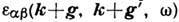 , к-рый представляет собой матрицу в пространстве векторов обратной решётки
g. В этом случае также можно ввести аналог продольной Д. п.:
, к-рый представляет собой матрицу в пространстве векторов обратной решётки
g. В этом случае также можно ввести аналог продольной Д. п.:Диэлектрическая постоянная - устаревшее название диэлектрической проницаемости.
Кристаллическая среда
характеризуется тензором Д. п. 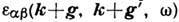 , к-рый представляет собой матрицу в пространстве векторов обратной решётки
g. В этом случае также можно ввести аналог продольной Д. п.:
, к-рый представляет собой матрицу в пространстве векторов обратной решётки
g. В этом случае также можно ввести аналог продольной Д. п.:
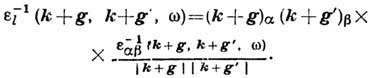
Обратная матрица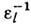 определяет потенциал взаимодействия
между статич. зарядами в среде. Матричный характер Д. п. ведёт к тому, что даже
"гладкое" внеш. воздействие
определяет потенциал взаимодействия
между статич. зарядами в среде. Матричный характер Д. п. ведёт к тому, что даже
"гладкое" внеш. воздействие 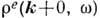 порождает быстро осциллирующие в пространстве компоненты
порождает быстро осциллирующие в пространстве компоненты 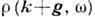 с произвольными значениями g. Среди них имеется и "гладкая"
компонента
с произвольными значениями g. Среди них имеется и "гладкая"
компонента 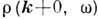 . Соотношение
между нею и
. Соотношение
между нею и 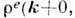
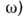 определяет т. н. макроскопич.
Д. п. кристалла:
определяет т. н. макроскопич.
Д. п. кристалла:
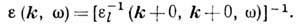
Хотя эта величина и не
описывает всех электродинамич. свойств кристалла, но она, как и соответствующий
тензор Д. п. 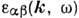 , даёт усреднённое (по объёмам, размер к-рых велик по сравнению с параметром
кристаллич. решётки, но мал по сравнению с величиной 1/k)описание свойств
кристалла. Именно величина
, даёт усреднённое (по объёмам, размер к-рых велик по сравнению с параметром
кристаллич. решётки, но мал по сравнению с величиной 1/k)описание свойств
кристалла. Именно величина 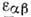 используется в кристаллофизике в качестве тензора Д. п.
используется в кристаллофизике в качестве тензора Д. п.
О. В. Долгов, Д. А. Киржниц, E. Г. Максимов.
Особенности диэлектрич. свойств плазмы определяются тем, что плазма является газом кулоновски
взаимодействующих частиц, поэтому в ней имеется самосогласованное поле, роль
к-рого в большинстве случаев заметно большая, чем роль столкновений. В плазме
доминирующую роль играют коллективные движения, приводящие к таким специфическим
эффектам, как бесстолкновительное затухание волн - затухание ,бесстолкновительные
процессы переноса. Сами же коллективные движения - колебания и волны - определяются
диэлектрич. свойствами плазмы. Д. п. плазмы, как анизотропной среды, связана
с тензором проводимости sab соотношением (система единиц СГ):
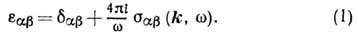
Проводимость плазмы 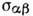 определяется с помощью решения кинетич. ур-ний для заряж. частиц относительно
их функций распределения fl (где l - сорт частицы). Знание
fl как функции частоты
определяется с помощью решения кинетич. ур-ний для заряж. частиц относительно
их функций распределения fl (где l - сорт частицы). Знание
fl как функции частоты 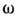 ,
волнового вектора k и самосогласованного электрич. поля E позволяет
найти ток
,
волнового вектора k и самосогласованного электрич. поля E позволяет
найти ток 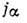 по
формуле
по
формуле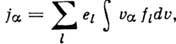 где
где 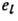 -
заряд,
-
заряд, 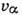 -
скорость частицы. В практически весьма важном случае относительно малых амплитуд
перем. полей задача о нахождении
-
скорость частицы. В практически весьма важном случае относительно малых амплитуд
перем. полей задача о нахождении 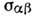 для однородной равновесной плазмы решается до конца. При этом кинетич. ур-ния
линеаризуются относительно малых амплитуд отклонений
для однородной равновесной плазмы решается до конца. При этом кинетич. ур-ния
линеаризуются относительно малых амплитуд отклонений 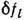 от стационарной функции распределения f0l. Используя (1) и линейные
относительно токов ур-ния Максвелла, для самосогласованных полей получают систему
линейных ур-ний, определяющих собственные колебания плазмы:
от стационарной функции распределения f0l. Используя (1) и линейные
относительно токов ур-ния Максвелла, для самосогласованных полей получают систему
линейных ур-ний, определяющих собственные колебания плазмы:
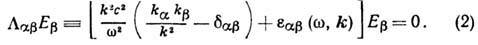
Решение системы (2) существует
в случае равенства нулю определителя системы
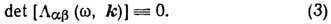
Решение ур-ния (3) позволяет
найти собственные частоты плазмы и дисперсионную зависимость 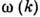 .
Если же решается задача о распространении волн в плазме (задана частота волны),
то (2) определяет волновой вектор Л как функцию
.
Если же решается задача о распространении волн в плазме (задана частота волны),
то (2) определяет волновой вектор Л как функцию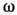 .
Ур-ние (3) даёт комплексные значения собственных частот, т. е.
.
Ур-ние (3) даёт комплексные значения собственных частот, т. е. 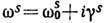 , где
, где 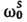 - частота
собственных колебаний,
- частота
собственных колебаний, 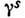 -
декремент их затухания. Для почти периодич. волн
-
декремент их затухания. Для почти периодич. волн 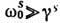 .
Отсюда можно сделать ряд общих выводов относительно поглощающих свойств
плазмы, используя лишь общий вид
.
Отсюда можно сделать ряд общих выводов относительно поглощающих свойств
плазмы, используя лишь общий вид 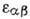 .
Действительно, энергия Q почти периодич. волны, поглощаемая в единицу
времени средой, определяется средним по периоду значением от скалярного произведения
плотности тока j на вектор электрич. поля волны E, т. е.
.
Действительно, энергия Q почти периодич. волны, поглощаемая в единицу
времени средой, определяется средним по периоду значением от скалярного произведения
плотности тока j на вектор электрич. поля волны E, т. е.

где 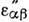 - антиэрмитова часть тензора Д. п., определяющая поглощение волны средой или
её затухание. В связи с малостью затухания эрмитова часть Д. п.
- антиэрмитова часть тензора Д. п., определяющая поглощение волны средой или
её затухание. В связи с малостью затухания эрмитова часть Д. п. 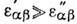 , поэтому найти собственные колебания плазмы можно методом теории возмущений.
В нулевом приближении в
, поэтому найти собственные колебания плазмы можно методом теории возмущений.
В нулевом приближении в  подставляется
подставляется
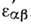 , а в след. приближении,
учитывая ортогональность собственных векторов эрмитовой задачи
, а в след. приближении,
учитывая ортогональность собственных векторов эрмитовой задачи 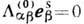 , находится декремент затухания с помощью ф-лы
, находится декремент затухания с помощью ф-лы
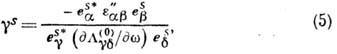
где 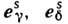 - соответствующие собственные векторы. Соотношения (1) - (5) справедливы
и для слабонеравновесных функций распределения.
- соответствующие собственные векторы. Соотношения (1) - (5) справедливы
и для слабонеравновесных функций распределения.
В общем случае при распространении
волн большой амплитуды задача о диэлектрич. свойствах плазмы резко осложняется
и решается лишь в отд. частных случаях. См. также Волны в плазме.

В. H. Ораевский
Релятивисты и позитивисты утверждают, что "мысленный эксперимент" весьма полезный интрумент для проверки теорий (также возникающих в нашем уме) на непротиворечивость. В этом они обманывают людей, так как любая проверка может осуществляться только независимым от объекта проверки источником. Сам заявитель гипотезы не может быть проверкой своего же заявления, так как причина самого этого заявления есть отсутствие видимых для заявителя противоречий в заявлении.
Это мы видим на примере СТО и ОТО, превратившихся в своеобразный вид религии, управляющей наукой и общественным мнением. Никакое количество фактов, противоречащих им, не может преодолеть формулу Эйнштейна: "Если факт не соответствует теории - измените факт" (В другом варианте " - Факт не соответствует теории? - Тем хуже для факта").
Максимально, на что может претендовать "мысленный эксперимент" - это только на внутреннюю непротиворечивость гипотезы в рамках собственной, часто отнюдь не истинной логики заявителя. Соответсвие практике это не проверяет. Настоящая проверка может состояться только в действительном физическом эксперименте.
Эксперимент на то и эксперимент, что он есть не изощрение мысли, а проверка мысли. Непротиворечивая внутри себя мысль не может сама себя проверить. Это доказано Куртом Гёделем.
Понятие "мысленный эксперимент" придумано специально спекулянтами - релятивистами для шулерской подмены реальной проверки мысли на практике (эксперимента) своим "честным словом". Подробнее читайте в FAQ по эфирной физике.
|
|