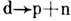 , и превращение
, и превращение 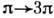 при рассеянии d и
при рассеянии d и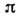 на атомных ядрах с малыми передачами импульса.
на атомных ядрах с малыми передачами импульса.Дифракционная диссоциация - процесс неупругого соударения адронов и атомных ядер,
в результате к-рого возбуждается один из адронов без изменения внутр. состояния
другого либо возбуждаются оба партнёра соударения (двойная Д. д.). Простейшие
примеры Д. д.- процесс развала быстрого дейтрона, 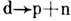 , и превращение
, и превращение 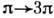 при рассеянии d и
при рассеянии d и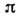 на атомных ядрах с малыми передачами импульса.
на атомных ядрах с малыми передачами импульса.
Феноменологически к Д.
д. относят такие неупругие и множественные процессы с участием адронов,
к-рые характеризуются след. свойствами: а) дифференц. сечения сильно вытянуты
вперёд, осн. часть процесса связана с малыми передачами импульса; б) сечения
почти не зависят от энергии, увеличиваясь при совсем высоких энергиях [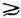 100
ГэВ в лаб. системе (л. с.)] пропорционально
100
ГэВ в лаб. системе (л. с.)] пропорционально 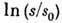 , где
, где 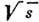 - энергия
в системе центра инерции (с. ц. и.) сталкивающихся частиц, а s0
- постоянная величина размерности квадрата энергии; в) между группами частиц
в конечном состоянии имеется большой незанятый интервал по быстротам; г)
сечения с участием частиц и античастиц на заданной мишени равны между собой;
д) в t-канале (где t - квадрат переданного 4-импульса) преобладают
обмены помероном; е) дифракц. амплитуды факторизуются, т. е. отношение
амплитуд для процессов
- энергия
в системе центра инерции (с. ц. и.) сталкивающихся частиц, а s0
- постоянная величина размерности квадрата энергии; в) между группами частиц
в конечном состоянии имеется большой незанятый интервал по быстротам; г)
сечения с участием частиц и античастиц на заданной мишени равны между собой;
д) в t-канале (где t - квадрат переданного 4-импульса) преобладают
обмены помероном; е) дифракц. амплитуды факторизуются, т. е. отношение
амплитуд для процессов 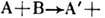
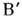 и
и 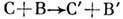 не зависит
от типа частиц В и В'; ж) в вершинах превращения
не зависит
от типа частиц В и В'; ж) в вершинах превращения 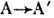 и
и 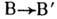 возможен обмен,
удовлетворяющий правилу
возможен обмен,
удовлетворяющий правилу 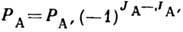 , где P - чётность, а J - спин частиц.
, где P - чётность, а J - спин частиц.
В процессе одиночной Д.
д. распределение по массам 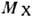 образующейся системы имеет пик у порога, само распределение занимает огранич.
интервал масс - наклон дифракц. конуса дифференц. сечения Д. д. сильно зависит
от
образующейся системы имеет пик у порога, само распределение занимает огранич.
интервал масс - наклон дифракц. конуса дифференц. сечения Д. д. сильно зависит
от 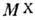 . Экспериментально
при Д. д. протона величина наклона сечения меняется от 20 ГэВ-2 до
4 ГэВ-2 при изменении
. Экспериментально
при Д. д. протона величина наклона сечения меняется от 20 ГэВ-2 до
4 ГэВ-2 при изменении 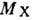 от 1,2 ГэВ до значений
от 1,2 ГэВ до значений 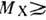 1,6
ГэВ (используется система единиц, в к-рой
1,6
ГэВ (используется система единиц, в к-рой 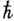 =с=1).
В области масс, больших чем в области образования резонансов, наклон определяется
=с=1).
В области масс, больших чем в области образования резонансов, наклон определяется
формфактором вершины, в
к-рой не происходит рождения частиц.
Так же, как и для (упругого)
дифракционного рассеяния, рассмотрение процессов Д. д. возможно как в
s-канале, когда изучаются переходы между собственными (диагональными) состояниями
рассеяния (т. е. состояниями, к-рые только поглощаются и рассеиваются упруго),
так и в t-канале, когда процесс определяется свойствами систем, к-рыми
адроны обмениваются при столкновении.
В картине s-канала Д. д. может быть сведена к дифракц. рассеянию собств. состояний, на к-рые можно разложить начальные и конечные состояния. В процессе рассеяния эти состояния по-разному поглощаются мишенью, что приводит к изменению волновой функции в конечном состоянии.
Для величины сечения Д.
д. справедливо неравенство

(предел Памплина; J. Pumplin,
1973). Здесь 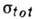 - полное сечение,
- полное сечение, 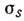 - сечение дифракц. рассеяния. Эксперим. данные при
- сечение дифракц. рассеяния. Эксперим. данные при 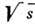 =53
ГэВ "насыщают" неравенство, приводя к значению ок. 13,5 мб для суммы
сечения однократной и двойной Д. д. Таким образом, Д. д. и дифракц. рассеяние
в сумме составляют приблизительно половину полного сечения.
=53
ГэВ "насыщают" неравенство, приводя к значению ок. 13,5 мб для суммы
сечения однократной и двойной Д. д. Таким образом, Д. д. и дифракц. рассеяние
в сумме составляют приблизительно половину полного сечения.
В картине t-канала
процесс упругой дифракции (дифракц. рассеяния) может быть представлен графиком,
изображённым на рис. 1 (волнистой линией помечен обмен доминирующим при высоких
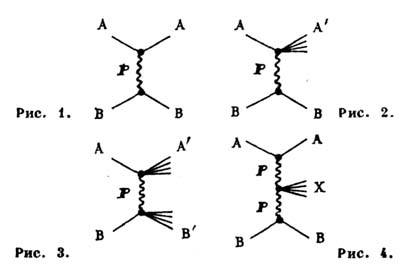
энергиях помероном 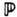 - носителем квантовых чисел вакуума). Однократной Д. д. соответствует диаграмма
на рис. 2, где возбуждение происходит только в одной вершине. Двойной Д. д.
соответствует диаграмма на рис. 3, когда возбуждение имеет место в обеих вершинах
взаимодействия. Процессу
- носителем квантовых чисел вакуума). Однократной Д. д. соответствует диаграмма
на рис. 2, где возбуждение происходит только в одной вершине. Двойной Д. д.
соответствует диаграмма на рис. 3, когда возбуждение имеет место в обеих вершинах
взаимодействия. Процессу 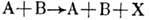 (где X - совокупность рождённых адронов) с двойным обменом помероном соответствует
диаграмма на рис. 4. Описание последнего процесса с помощью обмена двумя померонами
возможно при значительно больших энергиях, чем для процессов, представленных
диаграммами на рис. 1-3.
(где X - совокупность рождённых адронов) с двойным обменом помероном соответствует
диаграмма на рис. 4. Описание последнего процесса с помощью обмена двумя померонами
возможно при значительно больших энергиях, чем для процессов, представленных
диаграммами на рис. 1-3.
Условие когерентности при
соударении адронов высоких энергий (с адронами и атомными ядрами) является синонимом
дифракции. Если изменение импульса падающего адрона (массы т), умноженного
на продольный радиус взаимодействия, не превышает единицы, то конечная волновая
функция остаётся когерентной начальной волновой функции и происходит дифракция.
Для Д. д. протона это приводит к ограничению на область
масс MX образовавшейся системы частиц: 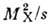 <0,1 В зависимости сечения инклюзивной Д. д. при малых передачах импульса
от
<0,1 В зависимости сечения инклюзивной Д. д. при малых передачах импульса
от 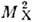 видны известные
возбуждения нуклона (рис. 5). Поведение инклюзивных сечений для диссоциации
протона как
видны известные
возбуждения нуклона (рис. 5). Поведение инклюзивных сечений для диссоциации
протона как 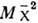 связано
со вкладом т. н. трёхпомеронного взаимодействия (см. Редже полюсов метод).
связано
со вкладом т. н. трёхпомеронного взаимодействия (см. Редже полюсов метод).
Двойную Д. д. кинематически
можно выделить, рассматривая распределения образовавшихся частиц по быстротам.
Вылетающие в процессе двойной Д. д. частицы концентрируются на краях интервала
быстрот, а расстояние по быстротам между группами частиц (кластерами) должно
быть больше нек-рого мин. значения. В отличие от распределения по массам, распределение
по 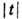 в Д. д. более
полого.
в Д. д. более
полого.
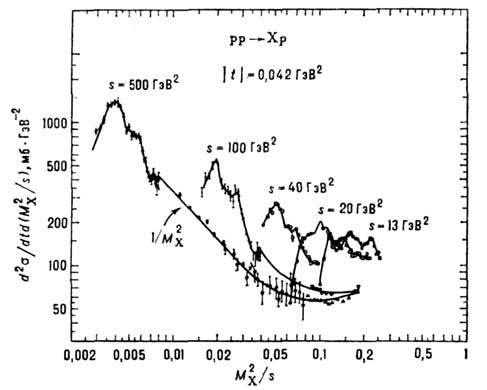
Рис. 5. Зависимость инвариантного
дифференциального сечения 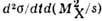 для процесса
для процесса 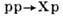 при
при 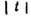 =0,042 ГэВ2
от
=0,042 ГэВ2
от 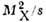 при различных
значениях s. C увеличением энергии оСласть резонансов сдвигается к меньшим
значениям
при различных
значениях s. C увеличением энергии оСласть резонансов сдвигается к меньшим
значениям  , тогда
как большие массы входят в область дифракции и сечения изменяются
, тогда
как большие массы входят в область дифракции и сечения изменяются 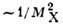 (разные значки - результаты различных экспериментов).
(разные значки - результаты различных экспериментов).
Двойной померонный обмен
экспериментально недостаточно изучен. Критич. проверкой природы обмена двумя
померонами было бы установление массового спектра центр. кластера, к-рый должен
характеризоваться изоспином I=0 и спином и чётностью 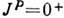 , 2+ , 4+,. . . В массовом спектре не должно быть одиночных
векторных мезонов. Однако на опыте они наблюдаются, вследствие чего возникает
вопрос о самом существовании двойного обмена померонами при достигнутых на ускорителях
энергиях частиц.
, 2+ , 4+,. . . В массовом спектре не должно быть одиночных
векторных мезонов. Однако на опыте они наблюдаются, вследствие чего возникает
вопрос о самом существовании двойного обмена померонами при достигнутых на ускорителях
энергиях частиц.

Л. И. Лапидус
|
|