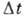Гаусса принцип. РЕАЛЬНАЯ ФИЗИКА. Глоссарий по физике

Гаусса принцип (принцип наименьшего принуждения) - вариационный принцип механики, устанавливающий одно из общих свойств движения механич. системы с любыми (голономными и неголономными) идеальными связями (см. Связи механические). Сформулирован К. Ф. Гауссом в 1829. Выражаемое Г. п. свойство движения связано с понятием о т. н. "принуждении" системы, вводимом след. образом. Если рассмотреть свободную материальную точку массой т, то она под действием заданной силы F совершит за промежуток времени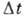

из положения А перемещение, определяемое с точностью до малых 3-го порядка вектором:

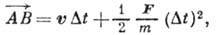
где

- скорость точки в положении А,

- ускорение, сообщаемое силой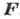

При наличии связей та же точка под действием той же силы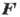

и реакции связи

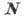получит какое-то др. ускорение

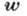(часть ускорения, равная

, будет точкой "потеряна") и совершит за время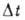

из того же положения А и при той же нач. скорости

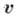др. перемещение:

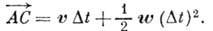
Разность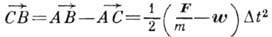

определяет вызванное действием связи отклонение точки от направления свободного движения, пропорциональное потерянному ускорению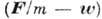

. Величина Z, равная сумме произведений масс всех точек системы на квадраты их потерянных ускорений, и наз., по Гауссу, "принуждением" системы:

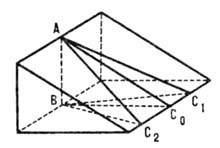
Г. п. устанавливает, что при идеальных удерживающих связях из всех кинематически возможных (допускаемых связями) движений, к-рые система может иметь, начиная перемещение из данной конфигурации с данными нач. скоростями, истинным будет то движение, для к-рого Z в каждый момент времени минимально. Напр., для частицы, движущейся вдоль наклонной плоскости под действием силы тяжести из положения А при v₀=0 (рис.), свободным будет пере мещение AB по вертикали, а кинематически возможным при данной связи - любое из перемещений AC₀, AC₁, AC₂, . . . вдоль наклонной плоскости. Следовательно, "принуждение" Z для частицы пропорционально квадрату величины BC_i, к-рая, очевидно, будет наименьшей для истинного перемещения AC₀(по линии наименьшего ската), что и утверждает Г. п.

Математически Г. п. выражается равенством

Z=0, в к-ром варьируются только ускорения точек системы; при этом предполагается, что силы от ускорения не зависят. Тогда из (1) можно получить др. выражение Г. п.: истинное движение механич. системы отличается от всех др. кинематически возможных движений, начинающихся из той же конфигурации и с теми же нач. скоростями, тем, что только для истинного движения в каждый данный момент времени справедливо равенство:

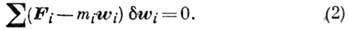
С помощью Г. п. можно получить дифференц. ур-ния движения любой механич. системы с идеальными связями. В частности, из него следует, что при отсутствии заданных сил точка будет двигаться вдоль данной гладкой поверхности по кривой, имеющей наименьшую кривизну. Это указывает на связь Г. п. с принципом прямейшего пути (см. Герца принцип).

Литература по принципу Гаусса

Знаете ли Вы, в чем ложность понятия "физический вакуум"?

Физический вакуум - понятие релятивистской квантовой физики, под ним там понимают низшее (основное) энергетическое состояние квантованного поля, обладающее нулевыми импульсом, моментом импульса и другими квантовыми числами. Физическим вакуумом релятивистские теоретики называют полностью лишённое вещества пространство, заполненное неизмеряемым, а значит, лишь воображаемым полем. Такое состояние по мнению релятивистов не является абсолютной пустотой, но пространством, заполненным некими фантомными (виртуальными) частицами. Релятивистская квантовая теория поля утверждает, что, в согласии с принципом неопределённости Гейзенберга, в физическом вакууме постоянно рождаются и исчезают виртуальные, то есть кажущиеся (кому кажущиеся?), частицы: происходят так называемые нулевые колебания полей. Виртуальные частицы физического вакуума, а следовательно, он сам, по определению не имеют системы отсчета, так как в противном случае нарушался бы принцип относительности Эйнштейна, на котором основывается теория относительности (то есть стала бы возможной абсолютная система измерения с отсчетом от частиц физического вакуума, что в свою очередь однозначно опровергло бы принцип относительности, на котором постороена СТО). Таким образом, физический вакуум и его частицы не есть элементы физического мира, но лишь элементы теории относительности, которые существуют не в реальном мире, но лишь в релятивистских формулах, нарушая при этом принцип причинности (возникают и исчезают беспричинно), принцип объективности (виртуальные частицы можно считать в зависимсоти от желания теоретика либо существующими, либо не существующими), принцип фактической измеримости (не наблюдаемы, не имеют своей ИСО).

Когда тот или иной физик использует понятие "физический вакуум", он либо не понимает абсурдности этого термина, либо лукавит, являясь скрытым или явным приверженцем релятивистской идеологии.

Понять абсурдность этого понятия легче всего обратившись к истокам его возникновения. Рождено оно было Полем Дираком в 1930-х, когда стало ясно, что отрицание эфира в чистом виде, как это делал великий математик, но посредственный физик Анри Пуанкаре, уже нельзя. Слишком много фактов противоречит этому.

Для защиты релятивизма Поль Дирак ввел афизическое и алогичное понятие отрицательной энергии, а затем и существование "моря" двух компенсирующих друг друга энергий в вакууме - положительной и отрицательной, а также "моря" компенсирующих друг друга частиц - виртуальных (то есть кажущихся) электронов и позитронов в вакууме.

Однако такая постановка является внутренне противоречивой (виртуальные частицы ненаблюдаемы и их по произволу можно считать в одном случае отсутствующими, а в другом - присутствующими) и противоречащей релятивизму (то есть отрицанию эфира, так как при наличии таких частиц в вакууме релятивизм уже просто невозможен). Подробнее читайте в FAQ по эфирной физике.