к библиотеке к оглавлению FAQ по эфирной физике ТОЭЭ ТЭЦ ТПОИ ТИ

РЕАЛЬНАЯ ФИЗИКА

Глоссарий по физике

А Б В Г Д Е Ж З И К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Ю Я

Гамильтона - Якоби уравнение

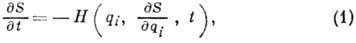
Гамильтона - Якоби уравнение - дифференциальное ур-ние в частных производных 1-го порядка, описывающее движение голономных механич. систем под действием потенц. сил. Чтобы составить Г.- Я. у., необходимо для данной механич. системы знать Гамильтона функцию H(q_i, p_i, t), где q_i и р_i- - канонич. переменные: обобщённые координаты и обобщённые импульсы, a t - время. Тогда Г.- Я. у. будет иметь вид

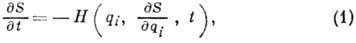
где правая часть представляет собой выражение функции H, в к-ром все p_i заменены на 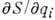, a S - подлежащая определению функция координат q_i и времени t, представляющая собой действие по Гамильтону; иногда функцию S (q_i, t)наз. главной функцией Гамильтона.

В частном случае при движении одной материальной точки в силовом поле, определяемом силовой функцией U(x, у, z, t), Г.- Я. у. имеет вид

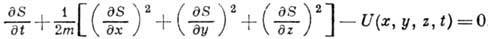где т - масса точки, х, у, z - её координаты.

Г.- Я. у. непосредственно связано с Гамильтона уравнениями ,к-рые с матем. точки зрения являются для ур-ния (1) ур-ниями характеристик.

Чтобы с помощью Г.- Я. у. найти закон движения механич. системы, надо определить полный интеграл ур-ния (1), т. е. его решение, содержащее столько постоянных интегрирования, сколько в ур-нии независимых переменных. Этими переменными являются координаты q_i и время t; число их равно s+1, где s - число степеней свободы системы. Следовательно, полный интеграл ур-ния (1) должен содержать s+l постоянную, из к-рых одна, как аддитивная, может быть отброшена, и имеет вид

Если решение Г.- Я. у. в виде (2) будет найдено, то, составив s равенств

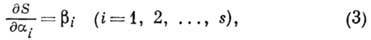
где 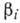- новые произвольные постоянные, получим s алгебраических (недифференциальных) ур-ний, левые части к-рых содержат q_i, 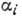и t и из к-рых можно определить q_i в виде

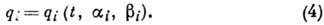
Значения др. группы канонич. переменных р_i находят из равенств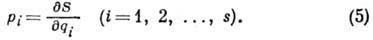

Ур-ния (4), выражающие q_i как функции t, и определяют положение механич. системы в любой момент времени, т. е. закон её движения. Входящие сюда постоянные 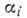и 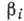находят подстановкой начальных данных в равенства (4) и (5).

Если функция Гамильтона H явно не содержит время, что, в частности, имеет место для консервативных систем, то S можно искать в виде

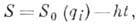
где h - постоянная, равная полной энергии системы, a S₀ - величина, наз. укороченным действием (действием по Лагранжу) или характеристич. функцией и определяемая как полный интеграл ур-ния в частных производных

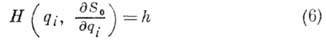
в виде 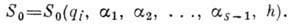Тогда полный интеграл Г.- Я. у. будет 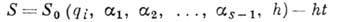и закон движения системы определится в соответствии с (3) из равенств

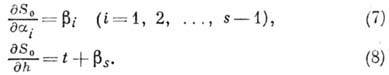
Ур-ния (7), содержащие в данном случае только q_i, 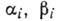и не содержащие время t, определяют в многомерном пространстве траекторию точки, изображающей данную механич. систему, а ур-ние (8) даёт закон движения вдоль этой траектории. Значения постоянных 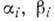определяются и в этом случае подстановкой начальных данных в равенстве (5), (7) и (8).

Г.- Я. у. и связанный с ним метод решения задач механики играют важную роль и в др. областях физики, особенно в оптике и квантовой механике. В частности, известное в геом. оптике ур-ние эйконала подобно Г--Я. у. в виде (6), где S₀ играет роль эйконала. Этот результат позволяет рассматривать классич. механику как аналог геом. оптики, в к-ром роль поверхностей движущейся волны играют поверхности S₀(q_i)=const, а роль световых лучей - ортогональные к этим поверхностям траектории движения.

С. M. Торг

к библиотеке к оглавлению FAQ по эфирной физике ТОЭЭ ТЭЦ ТПОИ ТИ

Знаете ли Вы, что, как и всякая идолопоклонническая религия, релятивизм представляет собой инструмент идеологического подчинения одних людей другим с помощью абсолютно бессовестной манипуляции их психикой для достижения интересов определенных групп людей, стоящих у руля этой воровской машины? Подробнее читайте в FAQ по эфирной физике.

НОВОСТИ ФОРУМА

Рыцари теории эфира