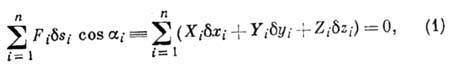
Принцип возможных перемещений (виртуальных перемещений принцип) - один из осн. принципов механики, выражающий
общее условие равновесия механич. системы. При рассмотрении условий равновесия
механич. системы методами геом. статики действие наложенных на систему связей
(см. Связи механические)учитывается введением соответствующих наперёд
неизвестных сил, наз. реакциями связей. Для сложных систем применение этого
метода приводит к необходимости решать большое число алгебраич. ур-ний со мн.
неизвестными. В методе решения задач статики, вытекающем из
принципа возможных перемещений, учёт наложенных
на систему связей производится введением понятия о т. н. возможных перемещениях системы из рассматриваемого положения. При этом в случае идеальных связей
вообще не возникает необходимости рассматривать реакции, что значительно облегчает
решение и расширяет класс разрешимых задач.
Условие равновесия, даваемое принципом возможных перемещений, гласит: для равновесия любой механич. системы с удерживающими идеальными
связями необходимо и достаточно, чтобы сумма элементарных работ действующих
на неё активных сил при любом возможном перемещении системы была равна нулю.
Математически принцип возможных перемещений выражается ур-нием:
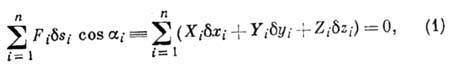
где Fi - равнодействующая всех активных сил, приложенных к i-й точке системы;
Xi, Yi, Zi - проекции силы Fi на оси прямоугольной системы координат;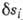
- модуль возможного перемещения s-й точки;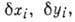
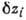- проекции этого перемещения
на те же оси; 
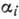- угол между направлениями силы и возможного перемещения.
Принцип возможных перемещений можно пользоваться
и при наличии в системе связей с трением, если силы трения включить в число
активных сил.
Принцип возможных перемещений применяется при
изучении условий равнове сия сложных механич. систем (механизмы, машины и др.).
Особенно просто с помощью принципа возможных перемещений находятся условия равновесия системы, имеющих
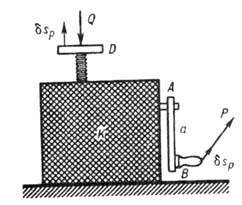
одну степень свободы (см. Степеней свободы число ).Напр., для подъёмного
механизма (рис.), детали к-рого скрыты в коробке К, ур-ние (1) даёт условие
равновесия:
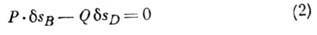
(P и Q - действующие
силы).
Связь между перемещениями
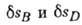можно установить,
если известно, что равномерному вращению рукоятки
АВ соответствует равномерный подъём винта D, причём за каждый
полный оборот рукоятки подъём винта равен h; тогда искомая связь даётся
пропорцией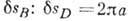 
: h, где а - длина рукоятки. Из ур-ния (2) определяется условие равновесия
механизма: Р=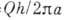
Методами геом. статики рассмотренная задача (если не будут указаны все детали
скрытого в коробке механизма) вообще решена быть не может. Для систем с неск.
степенями свободы ур-ния (1) можно составлять для каждого независимого перемещения
системы в отдельности.
Принцип возможных перемещений широко используются
также в статике деформируемых (твёрдых и жидких) тел. При этом учитываются все
действующие на тело объёмные и поверхностные силы, включая внутр. напряжения,
а суммирование в ур-ние (1) заменяется интегрированием соответственно но объёму
и поверхности тела.
О применении метода, аналогичного
даваемому принципом возможных перемещений к решению задач динамики, см. Д-Аламбера- Лагранжа
принцип.
С. M. Тарг
Дело в том, что в его постановке и выводах произведена подмена, аналогичная подмене в школьной шуточной задачке на сообразительность, в которой спрашивается:
- Cколько яблок на березе, если на одной ветке их 5, на другой ветке - 10 и так далее
При этом внимание учеников намеренно отвлекается от того основополагающего факта, что на березе яблоки не растут, в принципе.
В эксперименте Майкельсона ставится вопрос о движении эфира относительно покоящегося в лабораторной системе интерферометра. Однако, если мы ищем эфир, как базовую материю, из которой состоит всё вещество интерферометра, лаборатории, да и Земли в целом, то, естественно, эфир тоже будет неподвижен, так как земное вещество есть всего навсего определенным образом структурированный эфир, и никак не может двигаться относительно самого себя.
Удивительно, что этот цирковой трюк овладел на 120 лет умами физиков на полном серьезе, хотя его прототипы есть в сказках-небылицах всех народов всех времен, включая барона Мюнхаузена, вытащившего себя за волосы из болота, и призванных показать детям возможные жульничества и тем защитить их во взрослой жизни. Подробнее читайте в FAQ по эфирной физике.
|
|
 |
