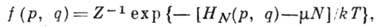
Большое каноническое распределение Гиббса - распределение вероятности состояний
статистич. ансамбля систем, к-рые находятся в тепловом и материальном равновесии
со средой (термостатом и резервуаром частиц) и могут обмениваться с ними энергией
и частицами при пост. объёме V; соответствует большому канонич. ансамблю Гиббса.
Большое каноническое распределение Гиббса установлено Дж. Гиббсом (J. W Gibbs) в 1901 как фундам.
закон статистич. физики (см. Гиббса распределения ).Равновесная функция
распределения f(p, q)зависит от координат и импульсов лишь через функцию
Гамильтона HN(p, q)системы N частиц:
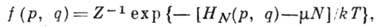
где T - абс. темп-pa,
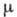- хим. потенциал,
Z - не зависящая от р, q величина, определяемая из условия нормировки:
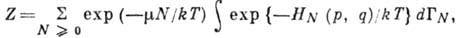
где суммирование ведётся
по всем целым положительным N, а интегрирование - по фазовому пространству
всех частиц:
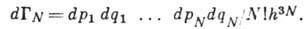
T. о., Z - функция от 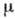, V, T и
выражается через статистич. интегралы для N частиц.
Большое каноническое распределение Гиббса можно вывести,
если рассматривать совокупность данной системы вместе с термостатом и резервуаром
частиц как одну большую, замкнутую и изолированную систему и применить к ней
микроканоническое распределение Гиббса .Тогда малая подсистема описывается
большим каноническим распределением Гиббса, к-рое можно найти интегрированием по фазовым переменным термостата
и резервуара частиц и суммированием по числам частиц (теорема Гиббса).
В квантовой статистике
статистич ансамбль характеризуется распределением вероятности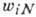
квантовых состояний г с энергией ,
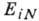соответствующих числу частиц N, с условием нормировки .
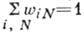Большое каноническое распределение Гиббса для квантовых
систем имеет вид:
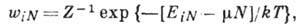
где Z - статистич.
сумма для большого канонич. ансамбля Гиббса, определяемая из условия нормировки
вероятности:
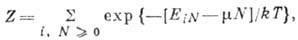
где суммирование ведётся
по всем квантовым состояниям допустимой симметрии и целым положительным N.
Большое каноническое распределение Гиббса в квантовом случае можно представить через статистич. оператор (матрицу плотности)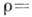
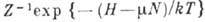, где H - гамильтониан системы.
Большое каноническое распределение Гиббса, как в классич.,
так и в квантовом случае, позволяет вычислить термодинамич. потенциал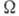
в переменных ,
V, T, равный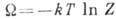
, где Z - статистич. сумма (или соотв. величина в классич. случае).
Большое каноническое распределение Гиббса особенно удобно для практич. вычислений, т. к. отсутствуют дополнит.
условия, связанные с постоянством энергии, как в микроканонич. распределении
Гиббса, или с постоянством числа частиц, как в канонич. распределении Гиббса.
Знаете ли Вы, что такое "Большой Взрыв"? Согласно рупору релятивистской идеологии Википедии "Большой взрыв (англ. Big Bang) - это космологическая модель, описывающая раннее развитие Вселенной, а именно - начало расширения Вселенной, перед которым Вселенная находилась в сингулярном состоянии. Обычно сейчас автоматически сочетают теорию Большого взрыва и модель горячей Вселенной, но эти концепции независимы и исторически существовало также представление о холодной начальной Вселенной вблизи Большого взрыва. Именно сочетание теории Большого взрыва с теорией горячей Вселенной, подкрепляемое существованием реликтового излучения..." В этой тираде количество нонсенсов (бессмыслиц) больше, чем количество предложений, иначе просто трудно запутать сознание обывателя до такой степени, чтобы он поверил в эту ахинею. На самом деле взорваться что-либо может только в уже имеющемся пространстве. Без этого никакого взрыва в принципе быть не может, так как "взрыв" - понятие, применимое только внутри уже имеющегося пространства. А раз так, то есть, если пространство вселенной уже было до БВ, то БВ не может быть началом Вселенной в принципе. Это во-первых. Во-вторых, Вселенная - это не обычный конечный объект с границами, это сама бесконечность во времени и пространстве. У нее нет начала и конца, а также пространственных границ уже по ее определению: она есть всё (потому и называется Вселенной). В третьих, фраза "представление о холодной начальной Вселенной вблизи Большого взрыва" тоже есть сплошной нонсенс. Что могло быть "вблизи Большого взрыва", если самой Вселенной там еще не было? Подробнее читайте в FAQ по эфирной физике.
- хим. потенциал,
Z - не зависящая от р, q величина, определяемая из условия нормировки:
, V, T и
выражается через статистич. интегралы для N частиц.
квантовых состояний г с энергией 
,
соответствующих числу частиц N, с условием нормировки 
.
Большое каноническое распределение Гиббса для квантовых
систем имеет вид:
, где H - гамильтониан системы.
в переменных 
,
V, T, равный 
, где Z - статистич. сумма (или соотв. величина в классич. случае).
Большое каноническое распределение Гиббса особенно удобно для практич. вычислений, т. к. отсутствуют дополнит.
условия, связанные с постоянством энергии, как в микроканонич. распределении
Гиббса, или с постоянством числа частиц, как в канонич. распределении Гиббса.
