|
|
|
Рис. 16.7 Модель с S-функцией mixedm |
И.В.Черных
Модель гибридной системы (комбинации непрерывной и дискретной системы) дана в файле mixedm.m . Рассматриваемая S-функция моделирует систему, состоящую из последовательно включенных интегратора (1/s) и блока задержки (1/z). Особенность S-функции для гибридной системы в том, что вызов callback-методов для расчета дискретной части системы выполняется в те же моменты времени, что и для непрерывной ее части, поэтому пользователь, при написании S-функции, должен предусмотреть проверку правильности вызова callback-методов рассчитывающих дискретную часть системы.
Ниже приведен текст этой S-функции.
S-функция dsfunc:
function [sys,x0,str,ts] = mixedm(t,x,u,flag)
% MIXEDM
Пример S-функции. S-функция моделирует систему, состоящую из%
последовательно включенных интегратора (1/s) и блока задержки (1/z).%
% Шаблон для создания S-функции - файл sfuntmpl.m .
%
% Copyright 1990-2001 The MathWorks, Inc.
% $Revision: 1.27 $
% Авторский перевод комментариев: Черных И.В.
%
Шаг модельного времени и смещение для дискретной части системы:dperiod = 1;
doffset = 0;
switch flag %
В зависимости от значения переменной flag происходит%
вызов того или иного метода:
%===============%
%
Инициализация %%===============%
case 0
[sys,x0,str,ts]=mdlInitializeSizes(dperiod,doffset);
%====================%
%
Расчет производных %%====================%
case 1
sys=mdlDerivatives(t,x,u);
%============================================================%
%
Расчет значений вектора состояний дискретной части системы %%============================================================%
case 2,
sys=mdlUpdate(t,x,u,dperiod,doffset);
%===========================================%
%
Расчет значений вектора выходных сигналов %%===========================================%
case 3
sys=mdlOutputs(t,x,u,doffset,dperiod);
%====================%
%
Завершение расчета %%====================%
case 9
sys = [];
%======================================%
%
Неизвестное значение переменной flag %%======================================%
otherwise
error(['unhandled flag = ',num2str(flag)]);
end
%
Окончание mixedm%===============================================================%
% mdlInitializeSizes %
%
Функция инициализации %%
Расчет начальных условий, значений вектора модельного времени,%%
размерности матриц %%===============================================================%
function [sys,x0,str,ts]=mdlInitializeSizes(dperiod,doffset)
sizes = simsizes;
sizes.NumContStates = 1; %
Число непрерывных переменных состояния.sizes.NumDiscStates = 1;
% Число дискретных переменных состояния.sizes.NumOutputs = 1;
% Число выходных переменных (размерность выходного%
вектора).sizes.NumInputs = 1;
% Число входных переменных (размерность входного%
вектора).sizes.DirFeedthrough = 0;
% Прямой проход. Прохода входного сигнала на выход%
нет.sizes.NumSampleTimes = 2;
% Размерность вектора шагов модельного времени.%
Шаги модельного времени задаются для непрерывной%
и для дискретной частей системы.sys = simsizes(sizes);
x0 = zeros(2,1);
% Задание вектора начальных значений переменных%
состояния.%
Начальные условия нулевыеstr = [];
% Параметр заразервирован для будущего%
использования.ts = [0 0];
% Шаг модельного времени для непрерывной части%
системы.dperiod doffset]; %
Шаг модельного времени для дискретной части%
системы.%
Окончание mdlInitializeSizes%
%========================================================================%
% mdlDerivatives %
% Функция для расчета значений производных вектора состояния непрерывной %
%
части системы %%========================================================================%
function sys=mdlDerivatives(t,x,u)
sys = u;
%
Окончание mdlDerivatives
%=========================================================================%
% mdlUpdate %
%
Функция для расчета значений вектора состояния дискретной части системы %%=========================================================================%
%
function sys=mdlUpdate(t,x,u,dperiod,doffset)
%
Расчет значения переменной состояния дискретной части системы%
выполняется в соостветствии с дискретным шагом расчета% (
погрешность по времени выбрана равной 1e-15).if abs(round((t - doffset)/dperiod) - (t - doffset)/dperiod) < 1e-15
sys = x(1);
else
sys = [];
end
%
Окончание mdlUpdate%
%========================================================%
% mdlOutputs %
%
Функция для расчета значений вектора выходных сигналов %%========================================================%
%
function sys=mdlOutputs(t,x,u,doffset,dperiod)
%
Расчет значения выходного сигнала системы%
выполняется в соостветствии с дискретным шагом расчета% (
погрешность по времени выбрана равной 1e-15).% Если условие, заданное оператором if истинно, то выходной сигнал блока
%
изменяется. В противном случае выходной сигнал остается равным значению%
на предыдущем шаге.%
if abs(round((t - doffset)/dperiod) - (t - doffset)/dperiod) < 1e-15
sys = x(2);
else
sys = [];
end
%
Окончание mdlOutputsПример модели с S-функцией mixedm приведен на рис.16.7.
|
|
|
Рис. 16.7 Модель с S-функцией mixedm |
16.7.6. Непрерывная модель электродвигателя постоянного тока независимого возбуждения
В данном параграфе на примере двигателя постоянного тока независимого возбуждения (ДПТ НВ) рассмотрим создание S-функции для модели реального объекта.
16.7.6.1. Математическое описание ДПТ НВ
Двигатель постоянного тока независимого возбуждения (рис. 16.9), описывается следующей системой дифференциальных и алгебраических уравнений в абсолютных единицах:
|
|
(1) |
|
|
(2) |
|
|
(3) |
|
|
(4) |
где
u - напряжение на якорной обмотке двигателя,
e - электродвижущая сила (ЭДС) якоря,
i - ток якоря,
Ф - поток, создаваемый обмоткой возбуждения,
M - электромагнитный момент двигателя,
MС - момент сопротивления движению,
![]()
R - активное сопротивление якорной цепи,
L - индуктивность якорной цепи,
J - суммарный момент инерции якоря и нагрузки,
С![]()
СМ
- коэффициент связи между током якоря и электромагнитным моментом.|
|
|
Рис. 16.9 Двигатель постоянного тока с независимым возбуждением. |
С точки зрения будущей модели, входными воздействиями являются напряжения якоря u и момент сопротивления движению MС , выходными переменными - электромагнитный момент двигателя M и скорость вращения вала двигателя ![]() , а переменными состояния - переменные стоящие под знаком производной: ток якоря i и скорость вращения вала двигателя
, а переменными состояния - переменные стоящие под знаком производной: ток якоря i и скорость вращения вала двигателя ![]() . Остальные переменные, входящие в состав уравнений (1) - (4) являются параметрами, численные значения которых, необходимо будет задавать при проведении расчетов.
. Остальные переменные, входящие в состав уравнений (1) - (4) являются параметрами, численные значения которых, необходимо будет задавать при проведении расчетов.
Преобразуем дифференциальные уравнения (1) и (2) к явной форме Коши и выполним подстановку. Система уравнений примет вид:
|
|
(5) |
|
|
(6) |
|
|
(7) |
|
|
(8) |
Последнее уравнение есть отражение того факта, что переменная состояния является также и выходной переменной.
Введем "машинные" переменные. Входные переменные:
![]() , .
, .![]() .
.
Выходные переменные:
![]() , .
, .![]() ,
,
Переменные состояния:
![]() ,
, ![]() .
.
Тогда уравнения (5) - (8) примут вид:
|
|
(9) |
|
|
(10) |
|
|
(11) |
|
|
(12) |
Перепишем систему уравнений в матричной форме:
|
|
(13) |
|
|
(14) |
где
|
|
|
|
Отметим, что в получившейся системе уравнений входные переменные не участвуют в формировании выходных переменных (матрица обхода D - отсутствует) и, следовательно, параметр sizes.DirFeedthrough, определяемый при инициализации S-функции должен быть задан равным нулю.
16.7.6.2. Пример S-функции для ДПТ НВ
Для создания S-функции для ДПТ НВ за основу взят файл примера модели непрерывной системы csfunc.m . Принципиальные отличия нового файла от образца сводятся к следующему:
Ниже приводится текст S-функции dpt_sfunc_1 (файл dpt_sfunc_1.m):
function [sys,x0,str,ts] = dpt_sfunc_1(t,x,u,flag,L,R,J,Cm,Cw,Fi)
% DPT_SFUNC_1 Пример S-функции для моделирования двигателя постоянного тока
%
независимого возбуждения.%
%
В примере выполняется моделирование с помощью уравнений%
пространства-состояния:% x' = Ax + Bu
% y = Cx + Du
%
% Copyright 2002, Chernykh ILya
% $Revision: 1.8
%
Автор: Черных И.В.%
%
Параметры S-функции, передаваемые через окно диалога блока S-function:%
% L - Индуктивность цепи якоря
% R -
Активное сопротивление цепи якоря% J -
Момент инерции% Cm -
Коэффициент связи между моментом и током% Cw -
Коэффициент связи между потоком и скоростью вращения вала% Fi -
Поток, создаваемый обмоткой возбуждения%
global A B C; %
Объявление глобальными переменных, необходимых для%
расчетов внутри функций mdlDerivatives и mdlOutputs .% Сами матрицы расчитываются в методе mdlInitializeSizes .
switch flag, % В зависимости от значения переменной flag происходит
%
вызов того или иного метода:%===============%
%
Инициализация %%===============%
case 0,
[sys,x0,str,ts]=mdlInitializeSizes(L,R,J,Cm,Cw,Fi);
%====================%
%
Расчет производных %%====================%
case 1,
sys=mdlDerivatives(t,x,u);
%===========================================%
%
Расчет значений вектора выходных сигналов %%===========================================%
case 3,
sys=mdlOutputs(t,x,u);
%=========================================%
%
Неиcпользуемые значения переменной flag %%=========================================%
case { 2, 4, 9 },
sys = [];
%======================================%
% Неизвестное значение переменной flag %
%======================================%
otherwise
error(['Unhandled flag = ',num2str(flag)]);
end
% Окончание dpt_sfunc_1
%===============================================================%
% mdlInitializeSizes %
%
Функция инициализации %%
Расчет начальных условий, значений вектора шагов модельного %%
времени,размерности матриц %%===============================================================%
function [sys,x0,str,ts]=mdlInitializeSizes(L,R,J,Cm,Cw,Fi)
sizes = simsizes
;sizes.NumContStates = 2; % Число непрерывных переменных состояния
%
В данном случае этот параметр равен 2% (
ток якоря и скорость вращения вала).sizes.NumDiscStates = 0
; % Число дискретных переменных состояния%
В данном случае этот параметр равен 0,%
поскольку модель непрерывная.sizes.NumOutputs = 2
; % Число выходных переменных (размерность выходного%
вектора). В данном случае этот параметр равен 2% (
скорость вращения и момент на валу).sizes.NumInputs = 2
; % Число входных переменных (размерность входного%
вектора). В данном случае этот параметр равен 2% (
напряжение на обмотке якоря и момент%
сопротивления).sizes.DirFeedthrough = 0
; % Прямой проход. Значение параметра равно нулю,%
поскольку матрица обхода D - отсутствует (входные%
переменные не участвуют в формировании выходных%
переменных).sizes.NumSampleTimes = 1
; % Размерность вектора модельного времени.sys = simsizes(sizes)
;x0 = zeros(2,1); % Задание вектора начальных значений переменных
%
состояния. Начальные условия нулевые.str = []
; % Зарезервированный параметрts = [0 0]
; % Матрица из двух колонок, задающая шаг модельного%
времени и смещение.%
Далее в функцию mdlInitializeSizes добавлены операторы для%
вычисления матриц A, B и C уравнений пространства состояния%
модели двигателя постоянного токаglobal A B C
; % Объявление глобальными переменных, необходимых для%
расчетов внутри функций mdlDerivatives и mdlOutputs.% Расчет матриц А,В и С:
%
A=[-R/L -Cw*Fi/L
Cm*Fi/J 0 ];
%
B=[1/L 0
0 -1/J];
%
C=[Cm*Fi 0
0 1];
% Окончание mdlInitializeSizes
%========================================================================%
% mdlDerivatives %
% Функция для расчета значений производных вектора состояния непрерывной %
%
части системы %%========================================================================%
function sys=mdlDerivatives(t,x,u)
%
global A B; %
Объявление глобальными переменных, необходимых для%
расчетов внутри метода.sys = A*x + B*u
;% Окончание mdlDerivatives
%========================================================%
% mdlOutputs %
% Функция для расчета значений вектора выходных сигналов %
%========================================================%
function sys=mdlOutputs(t,x,u)
global C
; % Объявление глобальными переменных, необходимых для%
расчетов внутри метода.sys = C*x
;% Окончание mdlOutputs
На рис.16.10 показаны модели двигателя постоянного тока на базе S-функции и с использованием стандартных блоков. Результаты расчета для обеих моделей идентичны. Окно диалога блока S-function изображено на рис. 16.11.
|
|
|
Рис. 16.10 Модели ДПТ НВ |
|
|
|
Рис. 16.11 Окно диалога блока S-function |
16.8. Создание S-функций на языке C с помощью S-Function Builder
Инструментарий Simulink предоставляет пользователю два способа создания S-функций на языке C: с помощью автоматического построителя S-Function Builder и вручную, с использованием шаблона (аналогично созданию S-функций на языке MATLAB). И хотя наибольшими возможностями обладает именно второй способ, первый способ прост и наименее трудоемок, и, поэтому именно с помощью S-Function Builder пользователь может легко и быстро создать нужную ему S-функцию. При этом как во втором, так и в первом случаях S-функция будет создана в виде исполняемого dll-файла, что обеспечивает повышенное быстродействие этой функции.
Создание S-функции рассмотрим на примере двигателя постоянного тока независимого возбуждения. Его математическое описание дано в п. 16.7.6.1. Поскольку в стандарте языка C отсутствуют матричные операции, то уравнения (9) - (12) перепишем в обычной форме:
|
|
(15) |
|
|
(16) |
|
|
(17) |
|
|
(18) |
Значения элементов матриц даны в п. 16.7.6.1.
S-Function Builder оформлен в виде обычного блока Simulink и находится в библиотеке Function&Tables (функции и таблицы). Пиктограмма блока показана на рис.16.12.
Рис. 16.12 Пиктограмма блока S-Function Builder
Двойной щелчок на пиктограмме открывает окно S - Function Builder . Окно S - Function Builder (см. рис. 16.13) содержит панель параметров ( Parameters), в которой находится графа для ввода имени S -функции ( S - function name ) и графа для ввода начальных значений параметров, передаваемых через окно диалога блока S - function ( S - function parameters ). Также на этой панели находится кнопка Build, предназначенная для запуска процесса компиляции S -функции . В нижней части окна S - Function Builder находятся кнопки Help (вызов справки) и Close / Cancel (закрыть окно).
Среднюю часть окна занимают шесть вкладок, предназначенных для задания свойств S -функции
и фрагментов ее кода:
1. Initialization - Инициализация. На вкладке Initialization задаются следующие свойства S -функции:
Окно S-Function Builder с открытой вкладкой Ininialization показано на рис.16.13. Для рассматриваемого примера число входных переменных равно двум (напряжение на обмотке якоря и момент сопротивления). Число выходных переменных равно двум (момент и скорость). Количество переменных состояния также равно двум (ток якоря и скорость). Число параметров S-функции, передаваемых через окно диалога равно 6 (см. п. 16.7.6.2), шаг модельного времени - наследуемый, число дискретных переменных состояния - 0, начальные значения дискретных и непрерывных переменных состояния нулевые.
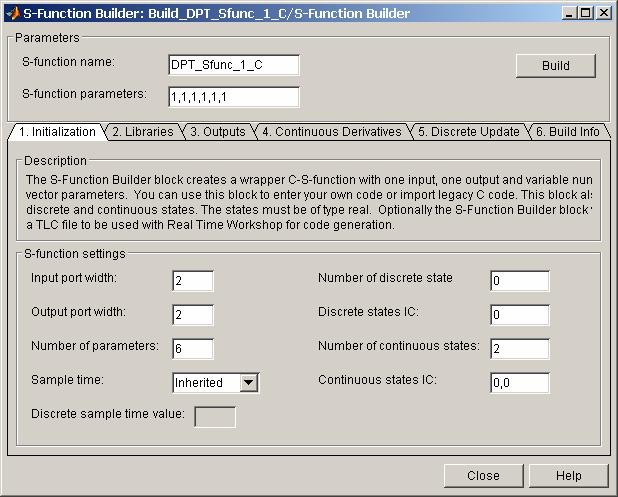
Рис. 16.13 Окно S-Function Builder (вкладка Ininialization)
2. Libraries - Библиотеки. На вкладке имеется три окна для ввода фрагментов С-кода:
Окно S - Function Builder с открытой вкладкой Libraries показано на рис. 16.14.
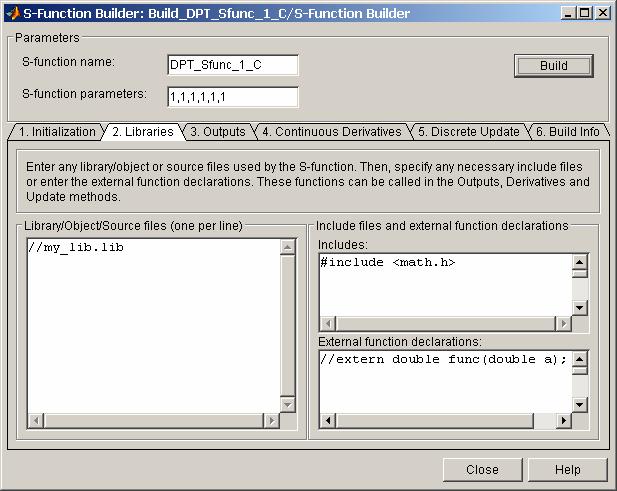
Рис. 16.14 Окно S-Function Builder ( вкладка Libraries)
3. Outputs - Выходы. Вкладка содержит текстовое окно, предназначенное для ввода выражений расчета выходных переменных. В расчетных выражениях можно использовать следующие переменные (не объявляя их специально):
На вкладке имеется флажок для установки параметра Inputs are needed in the output function ( direct feedthrough ) - использование входных сигналов для расчета выходных (прямой проход).
Текст автоматически генерируемого метода mdl Outputs , приведен ниже:
void sfun_Outputs_wrapper(const real_T *u,
real_T *y,
const real_T *xD, /* optional */
const real_T *xC, /* optional */
const real_T *param0, /* optional */
int_T p_width0 /* optional */
real_T *param1 /* optional */
int_t p_width1 /* optional */
int_T y_width, /* optional */
int_T u_width) /* optional */
{
/*
Место для ввода расчетного кода */} ,
где sfun - имя S -функции.
Окно S - Function Builder с открытой вкладкой Output s показано на рис. 16.15.

Рис. 16.15 Окно S-Function Builder (вкладка Outputs)
В примере на рис. 16.15 в первой строке объявляются переменные - параметры электродвигателя, и этим переменным присваиваются значения параметров передаваемых в S -функцию через окно диалога. Во второй строке объявляются и вычисляются переменные COO и С11, входящие в уравнения (17), (18). В третьей и четвертой строках записаны выражения для расчета выходных сигналов в соответствии с уравнениями (17) и (18). Параметр Inputs are needed in the output function ( direct feedthrough ) не установлен, поскольку в выражениях для расчета выходных сигналов отсутствуют входные. После генерации С-кода в тексте S-функции появится код, введенный в окне вкладки Outputs .
4. Continuous Derivatives - Производные непрерывных переменных состояния. Вкладка содержит текстовое окно, предназначенное для ввода выражений расчета производных непрерывных переменных состояния. В расчетных выражениях можно использовать те же переменные, что и на вкладке Outputs , за исключением дискретных переменных состояния xD . Сами производные обозначаются как dx [0], dx [1], dx [2] и т.п.
Текст автоматически генерируемого метода mdl Derivatives , приведен ниже:
void sfun_Derivatives_wrapper(const real_T *u,
const real_T *y,
real_T *dx,
real_T *xC,
const real_T *param0, /* optional */
int_T p_width0, /* optional */
real_T *param1,/* optional */
int_T p_width1, /* optional */
int_T y_width, /* optional */
int_T u_width) /* optional */
{
/*
Место для ввода расчетного кода */}
Окно S-Function Builder с открытой вкладкой Continuous Derivatives показано на рис . 16.15.
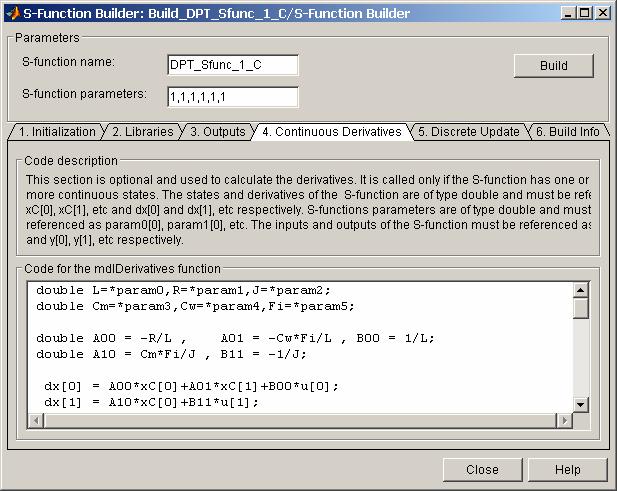
Рис . 16.16 Окно S-Function Builder ( вкладка Continuous Derivatives )
В примере на рис. 16.16 в первых двух строках объявляются переменные - параметры электродвигателя, и этим переменным присваиваются значения параметров передаваемых в S -функцию через окно диалога. В следующих двух строках объявляются и вычисляются переменные AOO … B 11 , входящие в уравнения (15), (16). В последних двух строках записаны выражения для расчета производных непрерывных переменных состояния в соответствии с уравнениями (15) и (16).
5. Discrete Update - Расчет дискретных переменных состояния. В текстовом окне вкладки записываются выражения для расчета дискретных переменных состояния. В расчетных выражениях можно использовать те же переменные, что и на вкладке Outputs , за исключением непрерывных переменных состояния x С . Сами дискретные переменные состояния обозначаются как xD [0], xD [1], xD [2] и т.п.
Текст автоматически генерируемо метода mdl Update , приведен ниже:
void sfun_Update_wrapper(const real_T *u,
const real_T *y,
real_T *xD,
const real_T *param0, /* optional */
int_T p_width0, /* optional */
real_T *param1,/* optional */
int_T p_width1, /* optional */
int_T y_width, /* optional */
int_T u_width) /* optional */
{
/*
Место для ввода расчетного кода */}
Окно S - Function Builder с открытой вкладкой Discrete Update показано на рис. 16.17.
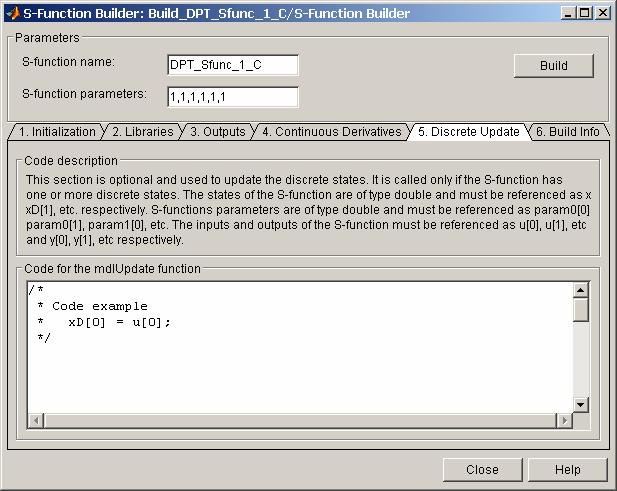
Рис . 16.17 Окно S-Function Builder ( вкладка Discrete Update ).
В рассматриваемом примере отсутствуют дискретные переменные состояния, поэтому на рисунке дан лишь пример расчетного выражения.
6. Build Info - Информация о компоновке. На вкладке в окне Compilation diagnostics (диагностические сообщения о ходе компиляции) отображается информацию о процессе компоновки S-функции .
На вкладке Build Info с помощью флажков можно установить следующие параметры:
Перед началом компиляции необходимо выбрать (настроить) компилятор. Для этого в командном окне MATLAB следует ввести команду:
mex - setup
и далее следовать диалогу с компилятором. С программой MATLAB поставляется компилятор Lcc . Ниже приводится пример такого диалога:
Please choose your compiler for building external interface (MEX) files:
Would you like mex to locate installed compilers [y]/n? n - Ответ пользователя
Select a compiler:
[1] Borland C++Builder version 5.0
[2] Borland C++Builder version 4.0
[3] Borland C++Builder version 3.0
[4] Borland C/C++ version 5.02
[5] Borland C/C++ version 5.0
[6] Borland C/C++ (free command line tools) version 5.5
[7] Compaq Visual Fortran version 6.1
[8] Compaq Visual Fortran version 6.5
[9] Digital Visual Fortran version 6.0
[10] Digital Visual Fortran version 5.0
[11] Lcc C version 2.4
[12] Microsoft Visual C/C++ version 6.0
[13] Microsoft Visual C/C++ version 5.0
[14] WATCOM C/C++ version 11
[15] WATCOM C/C++ version 10.6
[0] None
Compiler: 11 -
Ответ пользователяYour machine has a Lcc C compiler located at
C:\MATLAB6\sys\lcc. Do you want to use this compiler [y]/n? y - Ответ пользователя
Please verify your choices:
Compiler: Lcc C 2.4
Location: C:\MATLAB6\sys\lcc
Are these correct?([y]/n): y - Ответ пользователя
The default options file:
"C:\Documents and Settings\Администратор\Application Data\MathWorks\MATLAB\R12\mexopts.bat"
is being updated from C:\MATLAB6\BIN\WIN32\mexopts\lccopts.bat...
Процесс компиляции начинается после нажатия на кнопку Build . Об успешном завершении процесса компиляции свидетельствует сообщение вида:
### S-function 'DPT_Sfunc_1_C.dll' created successfully . По завершении процесса компиляции в рабочей папке будут созданы текстовые файлы с названиями вида:
sfun_C.c , sfun_wrapper.c и sfun.dll > . Последний является исполняемым файлом. В файле sfun _ C . c находится текст S -функции , а в файле sfun _ wrapper . c - методы, сгенерированные S- Function Builder .
Окно S - Function Builder с открытой вкладкой Build Info показано на рис. 16.18.
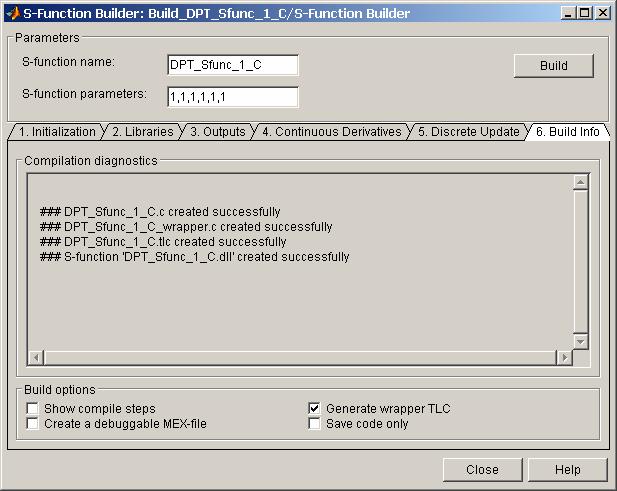
Рис . 16.18 Окно S-Function Builder ( вкладка Build Info ).
Результаты расчетов, выполненных с использованием созданной таким образом S -функции , полностью совпадают с результатами, приведенными в п. 16.7.6.2 . Скорость расчета модели с использованием S -функции , написанной на языке C в несколько раз выше, чем при использовании языка MATLAB .
|
|