И.В.Черных
Simulink Performance Tools включает четыре приложения, которые расширяют возможности Simulink и существенно увеличивают производительность программы. Использование этих инструментов может значительно повысить скорость процесса моделирования. Пользователь получает инструмент для сравнения разных вариантов модели, а также для быстрого тестирования модели.
Набор инструментов содержит:
15.1. Simulink Accelerator
Simulink Accelerator использует технологию генерации кода и пользовательский компилятор языка C для создания выполняемого файла (dll-файла), который заменяет интерактивный код, обычно используемый программой Simulink (в состав программы Simulink входит собственный компилятор lcc).
Simulink Accelerator обеспечивает:
Для перехода в ускоренный режим расчета необходимо в меню Simulation выбрать пункт Accelerator. После запуска модели на расчет будет произведена компиляция модели и выполнен расчет. При повторных запусках, если структура модели не менялась, компиляция выполнятся не будет, а будет сразу производиться расчет. При изменении параметров блоков повторная компиляция также не производится. Для возврата в обычный режим расчета следует меню Simulation выбрать пункт Normal.
При использовании ускоренного режима расчета следует иметь в виду, что модели, имеющие замкнутые алгебраические контуры, не могут быть рассчитаны в этом режиме.
15.2. Simulink Model Profiling
Simulink Model Profiling собирает данные о производительности в процессе выполнения модели и затем генерирует отчет, называемый профилем имитации на основании собранных данных. Этот отчет состоит из двух HTML-файлов: обобщающий файл и детальный файл. Обобщающий файл аккумулирует временную информацию и выводит ее в список, упорядоченный по временам выполнения для каждого метода. Детальный файл показывает, как много времени использует Simulink выполняя каждый метод, требующийся для моделирования, включая производные и основные методы.
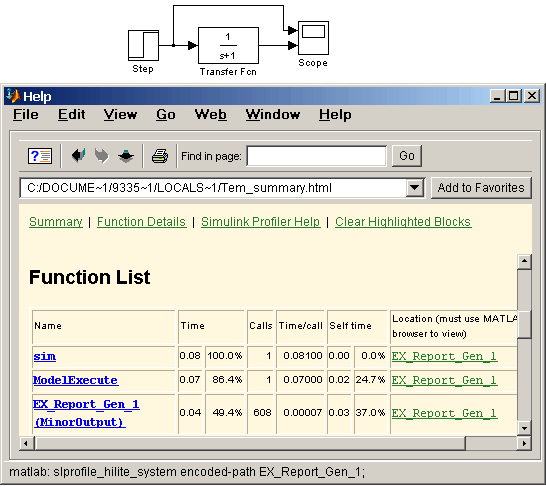
Для выполнения профилирования необходимо выполнить команду Profiler в меню Tools и запустить модель на расчет. По завершении расчета будет открыт файл отчета в окне справочной системы. Гиперссылки в отчете позволяют просмотреть детальную информацию для каждого метода. В результате пользователь может легко локализовать области модели, которые требуют наибольшего времени выполнения и быстро определить, где необходимо сконцентрировать усилия по оптимизации. На рис. 15.1 приведен пример модели и фрагмент отчета профилирования для нее.

Рис. 15.1 Пример модели и отчета профилирования.
15.3. Simulink Model Coverage
При разработке больших моделей, имеющих сложную логику переключения путей по которым распространяются сигналы, пользователь может столкнуться с проблемой тестирования модели. В ходе тестирования пользователь обычно пытается разработать тест, который охватывал бы все возможные пути, чтобы быть уверенным, что модель полностью проверена. Simulink Model Coverage помогает проверить эффективность подобных проверочных тестов. Используя Simulink Model Coverage, пользователь может интерпретировать поведение модели внутри индивидуальных блоков Simulink и объектов Stateflow, определить степень выполнения имитации (за счет вычисления количества выполнений каждого из блоков), а также идентифицировать избыточность или недостаточность частей модели. Для определения полноты тестирования модели возможна комбинация данных, полученных из разных имитаций.
Simulink Model Coverage обеспечивает:
Simulink Model Coverage позволит получить необходимый уровень тестирования разработки и определить количество тестов, необходимых для полной проверки. Анализ набора тестов в ходе разработки существенно уменьшает риск дефектов конструкции на поздних стадиях создания модели.
Для использования Simulink Model Coverage необходимо задать параметры отчета с помощью пункта Coverage Setting меню Tools. После выполнения моделирования будет открыт файл отчета в окне справочной системы.
На рис. 15.2 приведена схема модели и отчет, полученный я помощью Simulink Model Coverage. Из рисунка видно, что при данных параметрах схемы выполняется тестирования только 50% модели. Для полной проверки модели необходимо, чтобы сигнал, подаваемый на управляющий вход ключа менял свою полярность.
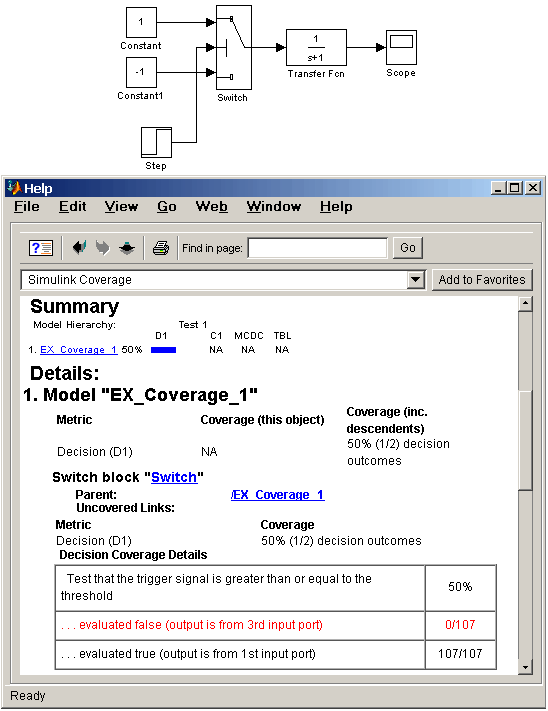
Рис. 15.2 Пример модели и отчета, полученного с помощью
Simulink Model Coverage
15.4. Simulink Model Differencing
Simulink Model Differencing сравнивает две Simulink-модели и генерирует графическое изображение различий между ними. На данном изображении выделяются одинаковые блоки моделей, имеющие различные атрибуты (красным цветом) и блоки, которые присутствуют только в одной из двух моделей (синим цветом). Пользователь может настроить изображение, чтобы просмотреть только блоки с графическими различиями, только блоки с неграфическими отличиями или блоки с любыми отличиями. Для выполнения сравнения моделей необходимо выполнить команду Model differences\Merge/Compare two models из меню Tools окна первой модели и в процессе диалога выбрать файл второй модели. Возможно также выполнить сравнение текущего состояния модели и ее последней записи на диске.
На рис. 15.3 показан пример сравнения моделей.

Рис. 15.3. Cравнение моделей с помощью Simulink Model Differencing
16. Simulink-функции
16.1. Введение
Simulink-функции (S-функции, S-functions) являются описанием блока на одном из языков программирования: MATLAB, C, C++, Ada, или Fortran. Набор стандартных блоков Simulink, достаточно обширен, однако в практике моделирования встречаются ситуации, когда нужного блока нет, либо структурное моделирование делает модель слишком сложной. В этом случае необходимо использовать технологию S-функций для создания нужного блока. С помощью языков программирования пользователь может создать описание сколь угодно сложного блока и подключить его к Simulink-модели, при этом с точки зрения взаимодействия пользователя с моделью, блок на основе S-функции ничем не отличается от стандартного библиотечного блока Simulink. Создаваемые блоки могут быть непрерывными, дискретными или гибридными. S-функции, созданные на C, C++, Ada или Fortran компилируются в исполняемые (*.dll) файлы, за счет чего обеспечивается повышенная скорость выполнения таких блоков. Такие S-функции обладают еще и дополнительными возможностями, которые включают работу с разными типами данных (целыми, действительными и комплексными числами различной степени точности), использование матриц в качестве входных и выходных переменных (MATLAB S-функции могут оперировать только векторами в качестве входных и выходных переменных), а также больший набор внутренних функций (сallback-методов).
Чаще всего S-функции используются при создании новых библиотечных блоков, блоков, обеспечивающих взаимодействие Simulink с аппаратными средствами компьютера, при создании блоков на основе математических уравнений, блоков реализующих анимационные возможности MATLAB, а также при подключении к модели Simulink существующего программного кода языков высокого уровня.
16.1. Блок S-function
S-функция подключается к модели Simulink с помощью библиотечного блока S-function (библиотека Functions&Tables). На рис. 16.1 показано окно модели с блоком S-function и его окно диалога.
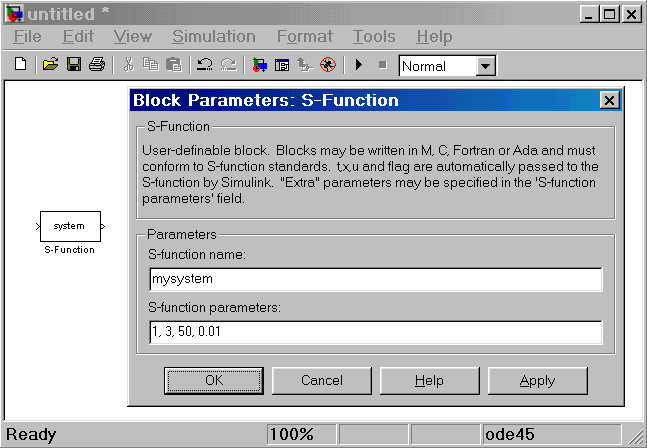
Рис. 16.1 Блок S-function и его окно диалога
Параметрами блока являются:
16.2. Математическое описание S-функции
Simulink-блок однозначно описывается наборами входных переменных u, переменных состояния x и выходных переменных y (рис. 16.2).
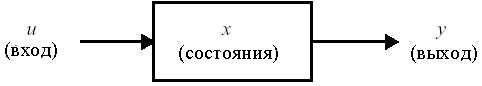
Рис. 16.2 Общий вид Simulink-блока
В математической форме блок можно описать в общем виде следующей системой уравнений:

16.3. Этапы моделирования
Процесс расчета модели выполняется Simulink в несколько этапов. На первом этапе выполняется инициализация модели: подключение библиотечных блоков к модели, определение размерностей сигналов, типов данных, величин шагов модельного времени, оценка параметров блоков, а также определяется порядок выполнения блоков и выполняется выделение памяти для проведения расчета. Затем Simulink начинает выполнять цикл моделирования. На каждом цикле моделирования (временном шаге) происходит расчет блоков в порядке, определенном на этапе инициализации. Для каждого блока, Simulink вызывает функции, которые вычисляют переменные состояния блока x, производные переменных состояния, и выходы y в течение текущего шага модельного времени. Этот процесс продолжается, пока моделирование не будет завершено. На рис. 16.3 показана диаграмма, иллюстрирующая этот процесс.

Рис. 16.3 Процесс моделирования
16.4. Callback-методы S-функции
Каждая задача при вызове S-функции в процессе моде моделирования решается с помощью специальной внутренней функцией (сallback-метода). В MATLAB S-функции используются следующие методы:
Если S-функция содержит непрерывные переменные состояния, Simulink вызывает сallback-методы mdlDerivatives и mdlOutputs для расчета производных переменных состояния и выходных переменных на внутренних шагах моделирования.
Вызов каждого из методов Simulink задает с помощью переменной flag, являющейся входным параметром S-функции.
16.5. Основные понятия S-функции
Для того, чтобы создать S-функцию правильно необходимо определить основные понятия, используемые в технологии создания S-функций. К эти понятиям относятся:
16.6. Создание S-функций на языке MATLAB
Наиболее простой и быстрый путь создать S-функцию – это написать ее на языке MATLAB с использованием файла-шаблона. И хотя создание S-функций на языке MATLAB имеет некоторые ограничения (например, MATLAB S-функция может иметь только по одному входному и выходному порту, а также передаваемые и принимаемые данные через эти порты могут быть только скалярами и векторами типа double), этот способ является наилучшим с точки зрения изучения механизма работы S-функции.
Ниже приводится шаблон S-функции с авторским переводом комментариев. Оригинальный файл шаблона sfuntmpl.m находится в папке ...\toolbox\simulink\blocks .
Шаблон MATLAB S-функции:
function [sys,x0,str,ts] = sfuntmpl(t,x,u,flag)
%
%
SFUNTMPL - Базовый шаблон для создания MATLAB S-функции.%
С помощью MATLAB S-функции пользователь может задать систему%
обыкновенных дифференциальных уравнений (ODE), уравнения дискретной%
системы, и(или) любой алгоритм, описывающий работу Simulink-блока.%
%
Базовая форма синтаксиса S-функции выглядит следующим образом:%
[sys,x0,str,ts] = sfunc(t,x,u,flag,p1,...,pn)%
% Параметры S-функции:
%
% t - Текущее время
% x
- Вектор переменных состояния системы% u
- Вектор входных сигналов% flag
- Флаг - целое число, определяющее какая функция внутри S-функции%
выполняется при вызове.% p1,...,pn
- Параметры S-функции, задаваемые в окне диалога%
блока "S-function".%
%
Результат, возвращаемый (вычисляемый) S-функцией в момент времени t% зависит от значения переменной flag, значения вектора состояния системы x
% и текущего значения вектора входного сигнала u.
%
% Результаты работы S-функции в зависимости от значения переменной flag
% приведены в таблице:
%
_________________________________________________________________________% | | | | |
% | flag | РЕЗУЛЬТАТ | ВЫПОЛНяЕМАя ФУНКЦИя | ОПИСАНИЕ |
% | | | (сallback-метод) | |
% |______|___________|________________________|_____________________________|
% | 0 | [sizes,x0,| mdlInitializesizes | Инициализация: Расчет |
%
| | str,ts] | | начальных условий, значений |%
| | | | вектора модельного времени |%
| | | | времени, размерности матриц.|%
| 1 | dx | mdlDerivatives | Расчет значений производных|%
| | | | вектора x состояния системы.|%
| 2 | ds | mdlUpdate | Расчет значений вектора |%
| | | | состояний x дискретной |%
| | | | системы: sys = x(n+1). |% | 3 | y | mdlOutputs | Расчет значений выходного |
%
| | | | вектора sys . |% | 4 | tnext | mdlGetTimeOfNextVarHit | Расчет значения времени для|
%
| | | | следующей расчетной точки |%
| | | | дискретной части системы. |%
| | | | Используется при расчете |%
| | | | дискретной или гибридной |%
| | | | системы с переменным шагом. |%
| 5 | | | Зарезервировано для будущего|%
| | | | использования. |%
| 9 | [] | mdlTerminate | Завершение расчета |%
|______|___________|________________________|_____________________________|%
%
% Параметры блока "S-function" p1,...,pn передаются в S-функцию при любом
%
значении переменной flag.%
% При вызове S-функции со значением переменной flag = 0 ею рассчитываются
%
следующие величины:%
% sys(1)
- Число непрерывных переменных состояния.% sys(2)
- Число дискретных переменных состояния.% sys(3)
- Число выходных переменных.% sys(4)
- Число входных переменных (размерность вектора u).% Любой из первых четырех элементов в sys может быть задан
%
равным -1 (минус один), что означает динамически задаваемую%
размерность соответствующих переменных. Фактическая размерность%
при вызове S-функции с другими значениями переменной flag%
будет равна размерности входного вектора u.% Например, при sys(3) = -1, размерность выходного вектора будет
%
задана равной размерности входного вектора.% sys(5)
- Значение зарезервировано для будущего использования.% sys(6)
- Значение, равное 1, соответствует прохождению входного сигнала%
на выход. Значение, равное 0, определяет, что входной сигнал не%
используется для вычисления выходного сигнала в функции% mdlOutputs
, вызываемой при значении переменной flag = 3.% sys(7) - Размерность вектора модельного времени (количество строк в
%
матрице ts).%
%
% x0 - Задание вектора начальных значений переменных состояния.
%
Если переменных состояния нет - значение параметра задается%
равным [] .%
% str - Зарезервированный параметр. Значение параметра задается
%
равным [] .%
% ts - Матрица, размерностью m-на-2, задающая модельное время
%
и смещение (period и offset), где m - число строк в матрице ts.%
% Например:
%
%
ts = [0 0, % Шаг модельного времени для непрерывной%
% части системы.% 0 1,
% Фиксированный шаг расчета для непрерывной%
% части системы.% period offset,
% Фиксированный шаг модельного времени для%
% дискретной части системы,%
% где - period > 0 & offset < PERIOD.% -2 0]; %
Переменный шаг модельного времени для%
дискретной части системы. При вызове%
S-функции со значением переменной flag = 4% выполняется расчет следующей точки по времени.
%
%
Если в матрице ts заданы несколько значений шага модельного времени,%
то его значения должны располагаться в порядке возрастания.%
В том случае, если задано более одного значения шага требуется проверка%
времени срабатывания блока в явном виде:%
abs(round((T-OFFSET)/PERIOD) - (T-OFFSET)/PERIOD)% Обычно задаваемая погрешность при проверке равна 1e-8. Она зависит от
%
величин шага модельного времени и времени окончания расчета.%
Можно также задать, чтобы значение временного шага передавалось в%
блок "S-function" из предшествующего блока модели. Для функций,%
изменяющихся внутри основного временного шага должно быть задано%
sys(7) = 1 и ts = [-1 0] .% Для функций, не изменяющихся внутри основного временного шага
%
должно быть задано sys(7) = 1 и ts = [-1 1] .%
% Copyright 1990-2001 The MathWorks, Inc.
% $Revision: 1.17 $
% Авторский перевод комментариев: Черных И.В.
%
%
Нижележащие строки показывают базовую структуру S-функции:%
switch flag, %
В зависимости от значения переменной flag происходит%
вызов того или иного метода::%
===============%% Инициализация %
%===============%
case 0,
[sys,x0,str,ts]=mdlInitializeSizes;
%====================%
% Расчет производных %
%
====================%case 1,
sys=mdlDerivatives(t,x,u);
%============================================================%
% Расчет значений вектора состояний дискретной части системы %
%============================================================%
case 2,
sys=mdlUpdate(t,x,u);
%=====================================================================%
% Расчет значений вектора выходных сигналов непрерывной части системы %
%
=====================================================================%case 3,
sys=mdlOutputs(t,x,u);
%
==================================================================%% Расчет значения времени для следующей расчетной точки дискретной %
%
части системы %%
==================================================================%case 4,
sys=mdlGetTimeOfNextVarHit(t,x,u);
%
====================%% Завершение расчета %
%
====================%case 9,
sys=mdlTerminate(t,x,u);
%
======================================%% Неизвестное значение переменной flag %
%======================================%
otherwise
error(['Unhandled flag = ',num2str(flag)]);
end
% Окончание функции sfuntmpl
%===============================================================%
% mdlInitializeSizes %
% Функция инициализации %
%
Расчет начальных условий, значений вектора модельного времени,%%
размерности матриц %%===============================================================%
function [sys,x0,str,ts]=mdlInitializeSizes
%
Приведенные ниже значения параметров даны в качестве примера и не отражают%
реально задаваемых значений.sizes = simsizes; %
Первый вызов функции simsizes создает структуру sizessizes.NumContStates = 0; %
Число непрерывных переменных состоянияsizes.NumDiscStates = 0; %
Число дискретных переменных состоянияsizes.NumOutputs = 0; %
Число выходных переменных (размерность выходного%
вектора)sizes.NumInputs = 0; %
Число входных переменных (размерность вектора u)sizes.DirFeedthrough = 1; % Параметр, задающий проход входного сигнала на
%
выход.%
Этот параметр нужно задавать равным 1, в том%
случае, если входной сигнал прямо или%
опосредованно(например, через логическое%
выражение или алгебраическую операцию)%
проходит на выход системы (иными словами: если%
входной сигнал u, входит в выражения задаваемые в%
функции mdlOutputs) или используется метод% mdlGetTimeOfNextVarHit.
%
При описании системы в уравнениях пространства%
состояний этот параметр следует задать равным 1,% если матрица D (матрица обхода) не пустая и
%
равным нулю, в противном случае.sizes.NumSampleTimes = 1; %
Размерность вектора модельного времени.%
Минимальное значение параметра = 1%
(одна строка в матрице ts).sys = simsizes(sizes); % Второй вызов функции simsizes. Данные о
%
размерностях передаются в Simulink.x0 = []; % Задание вектора начальных значений переменных состояния
% (
начальных условий).str = []; %
Задание параметра str, как пустой матрицы. Параметр%
заразервирован для будущего использования.ts = [0 0]; %
Матрица из двух колонок, задающая шаг модельного времени%
и смещение.%
Окончание mdlInitializeSizes
%
========================================================================%% mdlDerivatives %
% Функция для расчета значений производных вектора состояния непрерывной %
%
части системы %%========================================================================%
function sys=mdlDerivatives(t,x,u)
sys = [];
%
Окончание mdlDerivatives%
==========================================================================% % mdlUpdate %% Функция для расчета значений вектора выходных сигналов непрерывной части % % системы %
%
==========================================================================%function sys=mdlUpdate(t,x,u)
sys = [];
% Окончание mdlUpdate
%
===========================================================================%% mdlOutputs %
% Функция для расчета значений вектора выходных сигналов непрерывной части %
%
системы %%===========================================================================%
function sys=mdlOutputs(t,x,u)
sys = [];
%
Окончание mdlOutputs%===========================================================================%
% mdlGetTimeOfNextVarHit %
%
Расчет значения времени для следующей расчетной точки дискретной части %%
системы. %%
Функция рассчитывает время (абсолютное значение), по достижении которого %%
значения дискретной части системы передаютсяв Simulink-модель. %%
Функция используется только в случае моделирования дискретной части %%
системы с переменным шагом (variable discrete-time sample time). В этом %%
случае параметр ts функции mdlInitializeSizes должен быть задан как [-2 0]%%===========================================================================%
function sys=mdlGetTimeOfNextVarHit(t,x,u)
sampleTime = 1; % Пример: время срабатывания блока увеличивается
%
на 1 секунду.sys = t + sampleTime;
%
Окончание mdlGetTimeOfNextVarHit%
=========================================%% mdlTerminate %
% Функция, выполняющая завершение расчета %
%
=========================================%function sys=mdlTerminate(t,x,u)
sys = [];% Окончание mdlTerminate
16.7. Примеры S-функций языке MATLAB
16.7.1. Простейшая S-функция
Одним из самых простых примеров S-функций поставляемых с пакетом MATLAB является функция timestwo (файл timestwo.m). Данная S-функция выполняет умножение входного сигнала на коэффициент 2. Ниже приведен текст этой S-функции.
function [sys,x0,str,ts] = timestwo(t,x,u,flag)
%
% TIMESTWO - Пример S-функции. Выходной сигнал равен входному,
%
умноженному на 2:% y = 2 * u;
%
% Шаблон для создания S-функции - файл sfuntmpl.m .
%
% Copyright 1990-2001 The MathWorks, Inc.
% $Revision: 1.6 $
% Авторский перевод комментариев: Черных И.В.
%
switch flag, %
В зависимости от значения переменной flag происходит%
вызов того или иного метода:%===============%
%
Инициализация %%===============%
case 0
[sys,x0,str,ts]=mdlInitializeSizes;
%===========================================%
%
Расчет значений вектора выходных сигналов %%===========================================%
case 3
sys=mdlOutputs(t,x,u);
%=========================================%
%
Неиcпользуемые значения переменной flag %%=========================================%
% В примере не используются методы для завершения работы S-функции,
% нет непрерывных и дискретных переменных состояния,
%
поэтому значения переменной flag = 1, 2, 4, 9 не используются.%
Результатом S-функции в этом случае является пустая матрица.case { 1, 2, 4, 9 }
sys=[];
%======================================%
%
Неизвестное значение переменной flag %%======================================%
otherwise
error(['Unhandled flag = ',num2str(flag)]);
end
%
Окончание функции timestwo
%===============================================================%
% mdlInitializeSizes %
%
Функция инициализации %%
Расчет начальных условий, значений вектора шагов модельного %%
времени, размерности матриц %%=============================================================%
%
function [sys,x0,str,ts] = mdlInitializeSizes()
sizes = simsizes;
sizes.NumContStates = 0;
% Число непрерывных переменных состояния.sizes.NumDiscStates = 0;
% Число дискретных переменных состояния.sizes.NumOutputs = -1;
% Число выходных переменных (размерность выходного вектора).%
Динамическая размерность выходного вектора.sizes.NumInputs = -1;
% Число входных переменных (размерность входного%
вектора).%
Динамическая размерность входного вектора.sizes.DirFeedthrough = 1;
% Прямой проход. Есть проход входного сигнала%
на выход.sizes.NumSampleTimes = 1;
% Размерность вектора шагов модельного времени.sys = simsizes(sizes);
str = [];
% Параметр заразервирован для будущего%
использования.x0 = [];
% Задание вектора начальных значений переменных%
состояния.%
Переменных сомтояния нет, поэтому значение%
параметра - пустая матрица.ts = [-1 0];
% Матрица из двух колонок, задающая шаг%
модельного времени и смещение.%
Шаг наследуется из предшествуюшего блока.%
Окончание mdlInitializeSizes%
%========================================================%
% mdlOutputs %
%
Функция для расчета значений вектора выходных сигналов %%========================================================%
%
function sys = mdlOutputs(t,x,u)
sys = u * 2;
% Выходной сигнал блока есть входной сигнал, умноженный на%
коэффициент 2.%
Окончание mdlOutputsПример модели с S-функцией timestwo приведен на рис.16.4.
|
|
|
Рис. 16.4 Модель с S-функцией timestwo |
16.7.2. Модель непрерывной системы
Модель непрерывной системы, описываемой уравнениями пространства состояния дана в файле csfunc.m . Данная S-функция моделирует непрерывную систему с двумя входами, двумя выходами и двумя переменными состояния. Параметры модели (значения матриц A,В,С,D) задаются в теле S-функции и передаются в callback-методы через их заголовки в качестве дополнительных параметров.
Ниже приведен текст этой S-функции.
S-функция csfunc:
function [sys,x0,str,ts] = csfunc(t,x,u,flag)
% CSFUNC
Пример S-функции. Спомощью уравнений пространства состояния%
моделируется непрерывная система:%
% x' = Ax + Bu
% y = Cx + Du
%
%
Значения матриц передаются в callback-методы через их заголовки%
в качестве дополнительных параметров%
%
%
Шаблон для создания S-функции - файл sfuntmpl.m .%
% Copyright 1990-2001 The MathWorks, Inc.
% $Revision: 1.8 $
% Авторский перевод комментариев: Черных И.В.
%
Задание матриц:A=[-0.09 -0.01
1 0];
% Mатрица системы.B=[ 1 -7
0 -2]; % M
атрица входа.C=[ 0 2
1 -5];
% Mатрица выхода.D=[-3 0
1 0];
% Mатрица обхода.switch flag,
% В зависимости от значения переменной flag происходит%
вызов того или иного метода:%===============%
%
Инициализация %%===============%
case 0,
[sys,x0,str,ts]=mdlInitializeSizes(A,B,C,D);
%====================%
%
Расчет производных %%====================%
case 1,
sys=mdlDerivatives(t,x,u,A,B,C,D);
%===========================================%
%
Расчет значений вектора выходных сигналов %%===========================================%
case 3,
sys=mdlOutputs(t,x,u,A,B,C,D);
%=========================================%
%
Неиcпользуемые значения переменной flag %%=========================================%
% В примере не используются методы для завершения работы S-функции,
% нет дискретных переменных состояния,
%
поэтому значения переменной flag = 2, 4, 9 не используются.%
Результатом S-функции в этом случае является пустая матрица.case { 2, 4, 9 }
sys=[];
%======================================%
%
Неизвестное значение переменной flag %%======================================%
otherwise
error(['Unhandled flag = ',num2str(flag)]);
end
% Окончание csfunc
%
%===============================================================%
% mdlInitializeSizes %
%
Функция инициализации %%
Расчет начальных условий, значений вектора модельного времени,%%
размерности матриц %%===============================================================%
%
function [sys,x0,str,ts]=mdlInitializeSizes(A,B,C,D)
sizes = simsizes;
sizes.NumContStates = 2;
% Число непрерывных переменных состояния.sizes.NumDiscStates = 0;
% Число дискретных переменных состояния.sizes.NumOutputs = 2;
% Число выходных переменных (размерность выходного%
вектора).sizes.NumInputs = 2;
% Число входных переменных (размерность входного%
вектора).sizes.DirFeedthrough = 1;
% Прямой проход. Есть проход входного сигнала%
на выход.% (
матрица D не пустая).sizes.NumSampleTimes = 1; %
Размерность вектора шагов модельного времени.sys = simsizes(sizes);
x0 = zeros(2,1);
% Задание вектора начальных значений переменных%
состояния. Начальные условия нулевые.str = [];
% Параметр заразервирован для будущего%
использования.ts = [0 0];
% Матрица из двух колонок, задающая шаг модельного%
времени и смещение.%
Окончание mdlInitializeSizes%
%========================================================================%
% mdlDerivatives %
%
Функция для расчета значений производных вектора состояния непрерывной %%
части системы %%========================================================================%
%
function sys=mdlDerivatives(t,x,u,A,B,C,D)
sys = A*x + B*u;
%
Окончание mdlDerivatives%
%========================================================%
% mdlOutputs %
%
Функция для расчета значений вектора выходных сигналов %%========================================================%
function sys=mdlOutputs(t,x,u,A,B,C,D)
sys = C*x + D*u;
%
Окончание mdlOutputsПример модели с S-функцией csfunc приведен на рис.16.5.
|
|
|
Рис. 16.5 Модель с S-функцией csfunc |
16.7.3. Модель дискретнойной системы
Модель дискретной системы, описываемой уравнениями пространства состояния, дана в файле dsfunc.m . Данная S-функция моделирует дискретную систему с двумя входами, двумя выходами и двумя переменными состояния. Параметры модели (значения матриц A, В, С, D) задаются в теле S-функции и передаются в callback-методы через их заголовки в качестве дополнительных параметров.
Ниже приведен текст этой S-функции.
S-функция dsfunc:
function [sys,x0,str,ts] = dsfunc(t,x,u,flag)
% DSFUNC
Пример S-функции. С помощью уравнений пространства состояния%
моделируется дискретная система:% x(n+1) = Ax(n) + Bu(n)
% y(n) = Cx(n) + Du(n)
%
%
Значения матриц передаются в callback-методы через их заголовки%
в качестве дополнительных параметров%
%
Шаблон для создания S-функции - файл sfuntmpl.m .%
% Copyright 1990-2001 The MathWorks, Inc.
% $Revision: 1.8 $
% Авторский перевод комментариев: Черных И.В.
%
Задание матриц:A = [0.9135 0.1594
-0.7971 0.5947];
% Матрица системы.B = [0.05189 0
0.4782 0];
% Mатрица входа.C = [0 1
1 0];
% Mатрица выхода.D = [0.01 0
0 -0.02];
% Mатрица обхода.switch flag,
% В зависимости от значения переменной flag происходит%
вызов того или иного метода:%===============%
%
Инициализация %%===============%
case 0,
[sys,x0,str,ts] = mdlInitializeSizes(A,B,C,D);
%============================================================%
%
Расчет значений вектора состояний дискретной части системы %%============================================================%
case 2,
sys = mdlUpdate(t,x,u,A,B,C,D);
%=====================================================================%
%
Расчет значений вектора выходных сигналов непрерывной части системы %%=====================================================================%
case 3,
sys = mdlOutputs(t,x,u,A,C,D);
%=========================================%
%
Неиспользуемые значения переменной flag %%=========================================%
% В примере не используются методы для завершения работы S-функции,
% нет непрерывных переменных состояния,
%
поэтому значения переменной flag = 1, 4, 9 не используются.%
Результатом S-функции в этом случае является пустая матрица.case { 1, 4, 9 }
sys=[];
%======================================%
%
Неизвестное значение переменной flag %%======================================%
otherwise
error(['unhandled flag = ',num2str(flag)]);
end
%
Окончание dsfunc%
%===============================================================%
% mdlInitializeSizes %
%
Функция инициализации %%
Расчет начальных условий, значений вектора шагов модельного %%
времени, размерности матриц %%===============================================================%
%
function [sys,x0,str,ts] = mdlInitializeSizes(A,B,C,D)
sizes = simsizes;
sizes.NumContStates = 0; %
Число непрерывных переменных состояния.sizes.NumDiscStates = size(A,1);
% Число дискретных переменных состояния.sizes.NumOutputs = size(D,1);
% Число выходных переменных (размерность%
выходного вектора).sizes.NumInputs = size(D,2);
% Число входных переменных (размерность%
входного вектора).sizes.DirFeedthrough = 1;
% Прямой проход. Есть проход входного%
сигнала на выход (матрица D не пустая).sizes.NumSampleTimes = 1;
% Размерность вектора шагов модельного%
времени.sys = simsizes(sizes);
x0 = zeros(sizes.NumDiscStates,1); %
Задание вектора начальных значений%
переменных состояния.%
Начальные условия нулевыеstr = [];
% Параметр заразервирован для будущего%
использования.ts = [0.2 0];
% Матрица из двух колонок, задающая шаг%
модельного времени и смещение.%
Окончание mdlInitializeSizes%
%=========================================================================%
% mdlUpdate %
%
Функция для расчета значений вектора состояния дискретной части системы %%=========================================================================%
%
function sys = mdlUpdate(t,x,u,A,B,C,D)
sys = A*x+B*u;
%
Окончание mdlUpdate%========================================================%
% mdlOutputs %
%
Функция для расчета значений вектора выходных сигналов %%========================================================%
%
function sys = mdlOutputs(t,x,u,A,C,D)
sys = C*x+D*u;
%
Окончание mdlOutputsПример модели с S-функцией dsfunc приведен на рис.16.6.
|
|
|
Рис. 16.6 Модель с S-функцией dsfunc |
|
|