Пример. Рассмотрим в качестве примера, демонстрирующего использование процедуры интегрирования систем дифференциальных уравнений RKGS и сервисных процедур печати таблиц и графиков, программу решения системы уравнений, описывающих кинетику химического взаимодействия в соответствии с реакцией
![]()
Здесь Aj – символическое обозначение реагентов, k1 и k2 – константы скоростей соответствующих реакций.
В изотермических условиях константы скоростей постоянны и для режима идеального вытеснения
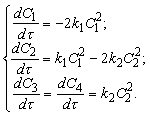
В приводимой программе решения системы дифференциальных уравнений предусмотрено разбиение всего интервала интегрирования на n участков длиной, равной шагу печати результатов. Ввод исходных данных осуществляется с помощью библиотечной функции ReadReal.
Program Kinetika;
Uses Mathlib, Crt;
(* Решение системы дифференциальных уравнений
первого порядка методом Рунге-Кутта *)
var
prmt : vector_5;
x : graph_x;
y : graph_y;
c, dery : vector_20;
aux : matrix_8_10;
k1, k2, k3, t0, tk, dt, nu,
sprint, empty : real;
i, j, ndim, n, ihlf : integer;
Procedure fct( x : real;
var c, dery : vector_20);
{Процедура, реализующая алгоритм вычисления производных }
begin
dery[1] := -2*k1*sqr(c[1]);
dery[2] := k1*sqr(c[1])-2*k2*sqr(c[2]);
dery[3] := k2*sqr(c[2]);
dery[4] := dery[3];
end;
begin
Clrscr;
nu := ReadReal('Число уравнений - ');
k1 := ReadReal('Константа скорости реакции k1 - ');
k2 := ReadReal('Константа скорости реакции k2 - ');
c[1] := ReadReal('Начальные условия: с[1] - ');
c[2] := ReadReal(' c[2] - ');
c[3] := ReadReal(' с[3] - ');
c[4] := ReadReal(' с[4] - ');
t0 := ReadReal('Начало отрезка интегрирования - ');
tk := ReadReal('Конец отрезка интегрирования - ');
dt := ReadReal('Начальный шаг интегрирования - ');
sprint := ReadReal('Шаг печати результатов - ');
ndim := Round(nu);
prmt[4] := 1.0E-3;
{ Начальная точка графика }
x[1] := t0;
for i := 1 to 4 do y[1,i] := c[i];
assign(output,'kinetika.res');
rewrite(output);
{ Вывод заголовка таблицы }
title(1,5,' t ',' c1 ',' c2 ',
' c3 ',' c4 ','','','','','');
{ Вывод строки с начальными условиями }
table(1,5,x[1],c[1],c[2],c[3],c[4],
empty,empty,empty,empty,empty);
n := Trunc((tk-t0)/sprint); { Число шагов расчета }
prmt[3] := dt; { Начальный шаг интегрирования }
prmt[5] := 0.0;
{ Интегрирование системы уравнений по шагам }
for i := 1 to n do begin
prmt[1] := (i-1)*sprint+t0;
prmt[2] := prmt[1]+sprint;
for j := 1 to ndim do
dery[j] := 1.0/ndim;
rkgs(prmt,c,dery,ndim,ihlf,fct,outp,aux);
{ Вывод строки таблицы для текущего шага }
table(1,5,prmt[2],c[1],c[2],c[3],c[4],
empty,empty,empty,empty,empty);
{ Накопление данных для графика }
x[i+1] := prmt[2];
y[i+1,1] := c[1];
y[i+1,2] := c[2];
y[i+1,3] := c[3];
end;
{ Вывод графика }
grafy(n+1,3,x,y);
end.
Результаты расчета будут иметь вид:
Т а б л и ц а 1
+---------+----------+-----------+----------+----------+
¦ ¦ ¦ ¦ ¦ ¦
¦ t ¦ c1 ¦ c2 ¦ c3 ¦ c4 ¦
¦ ¦ ¦ ¦ ¦ ¦
+---------¦----------¦-----------¦----------¦----------¦
¦ 0.0000 ¦ 1.0000 ¦ 0.1000 ¦ 0.0000 ¦ 0.0000 ¦
¦ 1.0000 ¦ 0.6250 ¦ 0.2703 ¦ 0.0086 ¦ 0.0086 ¦
¦ 2.0000 ¦ 0.4545 ¦ 0.3193 ¦ 0.0267 ¦ 0.0267 ¦
¦ 3.0000 ¦ 0.3571 ¦ 0.3259 ¦ 0.0478 ¦ 0.0478 ¦
¦ 4.0000 ¦ 0.2941 ¦ 0.3160 ¦ 0.0685 ¦ 0.0685 ¦
¦ 5.0000 ¦ 0.2500 ¦ 0.3000 ¦ 0.0875 ¦ 0.0875 ¦
¦ 6.0000 ¦ 0.2174 ¦ 0.2824 ¦ 0.1045 ¦ 0.1045 ¦
¦ 7.0000 ¦ 0.1923 ¦ 0.2650 ¦ 0.1194 ¦ 0.1194 ¦
¦ 8.0000 ¦ 0.1724 ¦ 0.2486 ¦ 0.1326 ¦ 0.1326 ¦
¦ 9.0000 ¦ 0.1562 ¦ 0.2334 ¦ 0.1442 ¦ 0.1442 ¦
¦ 10.0000 ¦ 0.1429 ¦ 0.2196 ¦ 0.1545 ¦ 0.1545 ¦
¦ 11.0000 ¦ 0.1316 ¦ 0.2071 ¦ 0.1636 ¦ 0.1636 ¦
¦ 12.0000 ¦ 0.1220 ¦ 0.1957 ¦ 0.1717 ¦ 0.1717 ¦
¦ 13.0000 ¦ 0.1136 ¦ 0.1853 ¦ 0.1789 ¦ 0.1789 ¦
¦ 14.0000 ¦ 0.1064 ¦ 0.1759 ¦ 0.1855 ¦ 0.1855 ¦
¦ 15.0000 ¦ 0.1000 ¦ 0.1673 ¦ 0.1913 ¦ 0.1913 ¦
+ - график функции F1(X)
# - график функции F2(X)
* - график функции F3(X)
X(I) Y(I)
0.0000 0.5000 1.0000
: : :
:+----:----:----:----:----:----:----:----:----:----:
0.00:* # +
1.00:* # +
2.00: * # +
3.00: * # +
4.00: * +#
5.00: * + #
6.00: * + #
7.00: * + #
8.00: * + #
9.00: * + #
10.00: + * #
11.00: + * #
12.00: + * #
13.00: + *
14.00: + *
15.00: + #*
:+----:----:----:----:----:----:----:----:----:----:
|
|