
Основные формулы для вычисления сумм последовательностей
Применение систем символьной математики особенно эффективно при решении задач математического анализа. Maple 7 обладает богатейшей базой данных по формулам математического анализа и может полноценно заменять тома книг со справочными данными. При этом важно, что Maple не только «знает» многие формулы, но и может успешно использовать их при решении достаточно сложных задач в аналитическом (символьном) виде.
Начнем рассмотрение таких операций с вычисления сумм последовательностей. Вычисление суммы членов некоторой последовательности f(k) при изменении целочисленного индекса k от значения m до значения n с шагом +1, то есть выражения:
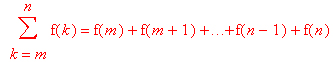
является достаточно распространенной операцией математического анализа. Для вычисляемой и инертной форм сумм последовательностей служат следующие функции:
sum(f.k): sum(f,k=m..n); sum(f,k=alpha):
Sum(f.k); Sum(f,k=m..n); Sum(f,k=a1pha);
Здесь f — функция, задающая члены суммируемого ряда, k — индекс суммирования, тип — целочисленные пределы изменения k, alpha — RootOf-выражение. Значение n может быть равно бесконечности. В этом случае для n используется обозначение ? или infinity.
Допустимо (а зачастую рекомендуется с целью исключения преждевременной оценки суммы) заключение f и k в прямые кавычки, например sum('f', 'k'=m. .n). Это сделано во всех примерах справочной системы Maple 7, относящихся к функции sum. Мы, однако, отказываемся от этого в тех случаях, когда результат идентичен при заключении f и k в кавычки и без такового. Во избежание путаницы, связанной с этой тонкостью синтаксиса функции sum, рекомендуется все примеры проверять после команды restart, убирающей предыдущие определения f и k.
Последовательности с заданным числом членов
Простейшими являются суммы последовательностей с фиксированным числом членов. Ниже даны примеры применения этих функций:
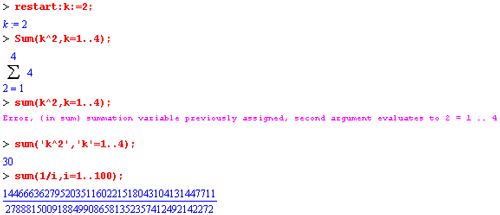
Обратите внимание, что во втором примере система отказалась от вычисления, а в третьем даже выдала сообщение об ошибке, связанной с тем, что переменной k перед вычислением сумм было присвоено численное значение 2. После заключения выражения и переменной индекса k в прямые кавычки ошибка исчезла, поскольку такая операция означает, что переменной придается неопределенное значение.
Особый класс образуют последовательности, у которых предел задается в общем виде значением переменной. Ниже представлен ряд последовательностей, у которых предел задается как 0.. n или 1.. n:

Такого рода последовательности, как видно из приведенных примеров, нередко имеют аналитические выражения для своего значения. Его вычисление намного проще, чем формирование заданной последовательности с прямым суммированием ее членов. Некоторые из таких сумм выражаются через специальные математические функции.
Суммы бесконечных последовательностей
Многие суммы бесконечных последовательностей сходятся к определенным численным или символьным значениям, и система Maple 7 способна их вычислять. Это поясняют следующие примеры:

Сумма от перемены мест слагаемых меняется!
Даже школьники хорошо знают, что от перестановки слагаемых сумма не изменяется. Однако Maple 7 (кстати, как и большинство других систем компьютерной математики) при вычислении сумм, увы, этому правилу не следует. Приведенные ниже примеры наглядно показывают этот просчет системы:

ВНИМАНИЕ
При вычислении сумм последовательностей надо строго соблюдать прямой (нарастающий) порядок задания значений индексной переменной суммы. Нарушение этого порядка чревато грубыми ошибками.
Могут встречаться множественные суммы по типу «сумма в сумме». Ограничимся приведением примера двойной суммы, имеющей аналитическое значение:

При конкретном значении N такую сумму нетрудно вычислить подстановкой:
> subs( N = 100, %);
8670850
Как видно из приведенных примеров, средства вычисления сумм последовательностей Maple 7 позволяют получать как численные, так и аналитические значения сумм, в том числе представляемые специальными математическими функциями.
Вычисление произведений членов последовательностей
Основные формулы для произведения членов последовательностей
Аналогичным образом для произведений членов f(i) некоторой последовательности, например вида:
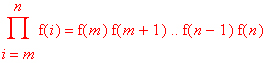
используются следующие функции:
product(f,k); product(f,k=m..n): product (f,k=alpha):
Product(f,k); Product(f,k=m..n): Product(f,k=alpha).
Обозначения параметров этих функций и их назначение соответствуют приведенным для функций вычисления сумм. Это относится, в частности, и к применению одиночных кавычек для f и k.
Примеры вычисления произведений членов последовательностей
Примеры применения функций вычисления произведений даны ниже:

Как и в случае вычисления сумм, вычисление произведений возможно как в численной, так и в аналитической форме — разумеется, если таковая существует. Это показывает следующий пример:

Нетрудно понять, что при i, стремящемся к бесконечности, перемножаемые члены последовательности стремятся к нулю, а потому к нулю стремится и их произведение. Вопросы доказательства подобных утверждений находятся за рамками данного учебного курса, ибо он посвящен не математике как таковой, а конкретной программе для математики — Maple 7.
От перемены места сомножителей произведение меняется!
Хотя произведение не зависит от порядка расположения сомножителей, их перестановка в Maple 7 недопустима. Это иллюстрируют следующие примеры:
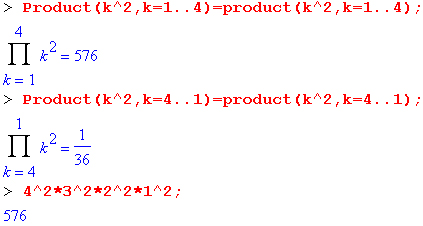
ВНИМАНИЕ
При вычислении произведений надо строго соблюдать прямой (нарастающий) поря-— док задания значений индексной переменной произведения. Нарушение этого порядка чревато грубыми ошибками.
Функции дифференцирования выражений diff и Diff
Вычисление производных функций fn(x) = dfn(x)/dxn n-го порядка — одна из самых распространенных задач математического анализа. Для ее реализации Maple 7 имеет следующие основные функции:
diff(a., xl, х2, .... xn) diff(a, [xl, х2, .... хn])
Diff(a, xl, x2, .... xn) Diff(a, [xl, x2, .... хn])
Здесь а — дифференцируемое алгебраическое выражение, властности функция f(xl. x2, .... хn) ряда переменных, по которым производится дифференцирование. Функция Diff является инертной формой вычисляемой функции diff и может использоваться для естественного воспроизведения производных в документах. Первая из этих функций (в вычисляемой и в инертной форме) вычисляет частные производные для выражения а по переменным xl, х2, ..., .хn. В простейшем случае diff(f(x),x) вычисляет первую производную функции f(x) по переменной х. При n, большем 1, вычисления производных выполняются рекурсивно, например diff (f (х), х, у) эквивалентно diff(diff (f(x), х), у). Оператор $ можно использовать для вычисления производных высокого порядка. Для этого после имени соответствующей переменной ставится этот оператор и указывается порядок производной. Например, выражение diff (f(x) ,x$4) вычисляет производную 4-го порядка и эквивалентно записи diff (f (х) ,х,х,х.х). A diff (g(x,y) ,x$2,y$3) эквивалентно diff(g(x,y),x,x.y,y,y) ;
Примеры вычисления производных:

Как видно из приведенных примеров, функции вычисления производных могут использоваться с параметрами, заданными списками. Приведенные ниже примеры показывают эти возможности и иллюстрируют дифференцирование функции пользователя для двух переменных:


Получаемые в результате дифференцирования выражения могут входить в другие выражения. Можно задавать их как функции пользователя и строить графики производных.
Для создания функций с производными может также использоваться дифференциальный оператор D. Порою он позволяет создавать более компактные выражения, чем функции diff и Diff. Дифференциальный оператор можно записывать в следующих формах: D(f) или D[i](f), где параметр f — выражение или имя функции, i — положительное целое число, выражение или последовательность. Оператор D(f) просто вычисляет имя производной от f, поскольку в этой форме он эквивалентен unnaplyCdiff (f (х) ,х) ,х). В форме D(f) (х) этот оператор подобен diff (f (x) ,x).
Приведем примеры дифференцирования функций, заданных только именами, и функций с одним параметром:

Следующий пример показывает дифференцирование функции пользователя fun с применением дифференциального оператора D и функции diff:
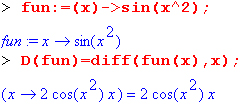
Дифференциальный оператор можно применять и для дифференцирования функций нескольких переменных по заданной переменной:
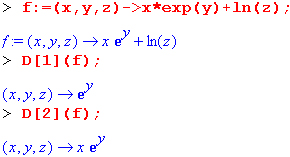
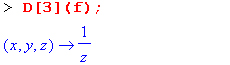
Пример применения дифференциального оператора для функции f, заданной программным объектом-процедурой, представлен ниже:

Этот пример показывает реализацию схемы Горнера для полинома b степени n от переменной х. При этом применение оператора дифференцирования возвращает процедуру. Ряд интересных возможностей по вычислению производных предоставляет пакет расширения student.
Вычисление неопределенных интегралов
Вычисление неопределенного интеграла обычно заключается в нахождении первообразной функции. Это одна из широко распространенных операций математического анализа.
Для вычисления неопределенных и определенных интегралов Maple V предоставляет следующие функции:
int(f.x); int(f.x=a..b); int(f.x-a..b,continuous):
Int(f.x); Int(f,x=a..b): Int(f,x=a..b,continuous):
Здесь f — подынтегральная функция, х — переменная, по которой выполняются вычисления, а и b — нижний и верхний пределы интегрирования, continuous — необязательное дополнительное условие.
Maple 7 старается найти аналитическое значение интеграла с заданной подынтегральной функцией, Если это не удается (например, для «не берущихся» интегралов), то возвращается исходная запись интеграла. Для вычисления определенного интеграла надо использовать функцию evalf(int(f ,х=а. .b)). Ниже приведены примеры вычисления интегралов:

Обратите внимание, что в аналитическом представлении неопределенных интегралов отсутствует произвольная постоянная С. Не следует забывать о ее существовании. Для вычисления кратных интегралов (двойных, тройных и т. д.) следует применять функцию int (или Int) внутри такой же функции, делая это столько раз, сколько нужно. В отличие от функции дифференцирования для функции интегрирования нельзя задавать подынтегральные функции в виде списка или множества. Возможно вычисление сумм интегралов и интегралов сумм, а также интегралов от полиномов:

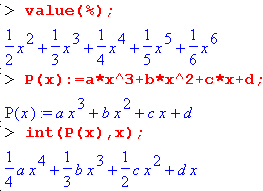
ПРИМЕЧАНИЕ
Maple 7 успешно берет большинство справочных интегралов. Но не всегда форма представления интеграла совпадает с приведенной в справочнике. Иногда требуется доводка ее до нужной формы, а иногда Maple 7 упорно дает иное выражение (в большинстве случаев правильное). Тем не менее следует помнить, что всегда может найтись интеграл, который окажется «не по зубам» и Maple 7.
Конвертирование и преобразование интегралов
В некоторых случаях Maple 7 не может вычислить интеграл. Тогда она просто повторяет его. С помощью функций taylor и convert можно попытаться получить аналитическое решение в виде полинома умеренной степени, что демонстрирует следующий характерный пример:

Естественно, что в этом случае решение является приближенным, но оно все же есть и с ним можно работать, например построить график функции, представляющей данный интеграл.
Система Maple непрерывно совершенствуется. Например, в Maple V R4 интеграл с подынтегральной функцией ехр(x^4) не брался, а система Maple 7 с легкостью берет его:
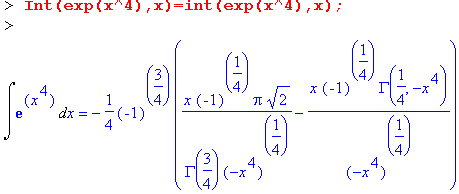
Хотя полученный результат, выраженный через гамма- функцию, нельзя назвать очень простым, но он существует и с ним также можно работать. Например, можно попытаться несколько упростить его, используя функцию simplify:
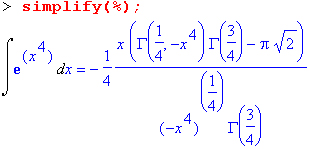
Разумеется, существует также множество иных возможностей и приемов для выполнения операции интегрирования. В дальнейшем мы неоднократно будем рассматривать и другие, более специфические функции для осуществления интегрирования и вычисления интегральных преобразований. В частности, ряд средств вычисления интегралов реализован в пакете student.
Вычисление определенных интегралов
Другой важной операцией является нахождение в аналитической или численной форме определенного интеграла:
Определенный интеграл удобно трактовать как площадь, ограниченную кривой f(x), осью абсцисс и вертикалями с координатами, равными а и b. При этом площадь ниже оси абсцисс считается отрицательной. Таким образом, значение определенного интеграла — это число или вычисляемое выражение.
Для вычисления определенных интегралов используются те же функции int и Int, в которых надо указать пределы интегрирования, например х=а.. b, если интегрируется функция переменной х. Это поясняется приведенными ниже примерами:


Как видно из этих примеров, среди значений пределов может быть бесконечность, обозначаемая как infinity.
Каверзные интегралы и визуализация результатов интегрирования
Выше мы уже сталкивались с примерами вычисления «каверзных» интегралов. Немного продолжим эту важную тему и заодно рассмотрим приемы визуализации вычислений, облегчающие понимание их сущности.
В Соросовском образовательном журнале (№ 6, 2000, с. 110) приводятся не совсем удачные примеры вычислений определенного интеграла с применением системы Mathematica, при которых якобы встречаются настолько большие трудности, что они не под силу любому калькулятору или компьютеру. При некоторых попытках вычисления этого интеграла он давал нулевое значение. Но Maple 7 (кстати, как и Mathematica 4) с легкостью берет этот интеграл и позволяет сразу и без какой-либо настройки вычислить для него как точное, так и приближенное значение:

Хотя первое из решений является самым кратким и, скорее всего, единственным точным решением, оно может и должно насторожить опытного пользователя. Дело в том, что в полученном выражении фигурируют большие числа, и потому для правильного приближенного решения (в виде вещественного числа в научной нотации) нужно заведомо использовать аппарат точной арифметики и ни в коем случае не полагаться на погрешность, заданную по умолчанию, — вот в чем основная ошибка в упомянутой статье.
Именно поэтому левая и правая части приближенного решения (выполненного с точностью до 30 цифр) заметно различаются. Знак равенства между ними вызывает чувство протеста у истинных математиков. На самом деле, не надо забывать, что знак равенства здесь был введен просто как текстовый комментарий, — вы можете попробовать сами заменить его на более приемлемый здесь знак приближенного равенства. Любопытно, что предшествующая версия Maple 6 при задании погрешности по умолчанию вычисляла значение этого интеграла также как 0, тогда как Maple 7 «поумнела» уже настолько, что дает значение 0.01835046770 даже в этом случае.
При таких условиях многие читатели могут сомневаться в корректности конечного результата. Между тем Maple 7 позволяет наглядно проиллюстрировать характер промежуточных вычислений подобных интегралов. Например, для этого можно вычислить неопределенный интеграл подобного вида:

Нетрудно заметить, что решение распадается на множество слагаемых, соответствующих общеизвестному интегрированию по частям. В каждом слагаемом имеются большие числа, и потому принципиально необходимо применение арифметики высокой точности (или разрядности). Maple 7 такими средствами, причем превосходными, обладает.
Продолжим изучение данного «каверзного» интеграла. Опробуем силы Maple 7 на интеграле более общего вида, где конкретный показатель степени заменен на обобщенный —п. Здесь нас ожидает приятный сюрприз — Maple 7 с легкостью выдает аналитическое решение для данного определенного интеграла:


Однако радоваться несколько преждевременно. Многие ли математики знают, что это за специальная функция — WhittakerM? Студенты, любящие подшучивать над своим профессором, могут попробовать спросить у него об этом. Скорее всего, профессор стушуется, а потом будет долго копаться в литературе, прежде чем найдет ее определение и сможет разъяснить, что это такое. Но хуже другое — Maple 7 при конкретном n = 20 дает грубо неверное решение — 0 (почему — уже объяснялось). Забавно, что при этом сама по себе функция WhittakerM вычисляется для n = 20 без проблем:
> WhittakerM(10,10.5.1);
6353509348
А теперь присмотритесь к новому результату вычисления злополучного интеграла. Оказывается, он уже не содержит больших чисел, свойственных прямому решению! Зная значение WhittakerM с погрешностью по умолчанию, можно уверенно вычислить приближенное численное значение интеграла с тойже погрешностью, уже не прибегая к арифметике высокой точности:
> (exp(-.5)*WihittakerM(10,10.5.1))/21;
01835046770
Итак, мы вычислили нужный интеграл несколькими разными способами. В этом и проявляется могущество современной математики, достойно представленной такими системами, как Maple 7. Заинтересованный читатель может попытаться найти еще ряд методов решения данного интеграла и преуспеть в этом! Мы же как торжество Maple 7 приведем график зависимости значений данного интеграла от показателя степени n при его изменении от 0 до 50 (рис. 8.1). Надо ли говорить о том, что полученный результат имеет куда более важное значение, чем вычисление нашего злополучного интеграла при конкретном n = 20? А плавный ход графика показывает, что в вычислении данного интеграла нет никаких признаков неустойчивости решения при изменении n, если соблюдать правило выбора погрешности вычислений.
Наличие у функции особых (сингулярных) точек нередко затрудняет выполнение с ней ряда операций, таких как численное интегрирование. В этом случае могут помочь соответствующие параметры. Например, вычисление следующего интеграла дает явно неудобное выражение в виде набора значений, разных для разных интервалов измененияа:

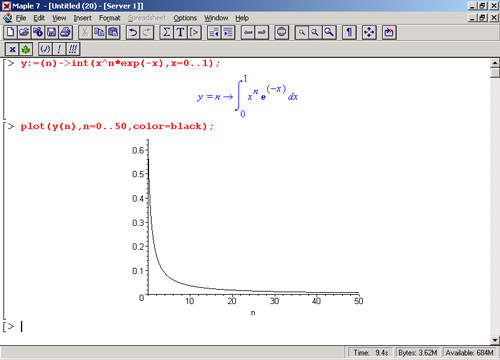
Рис. 8.1. Значение интеграла от х^n*ехр(-х) как функция n
Увы, попытка вычислить по этому выражению значение интеграла не всегда дает корректный результат. Например, при х от -2 до 0 получаются бесконечные значения. Да и график зависимости значения интеграла от параметра a имеет подозрительный вид (рис. 8.2). Это как раз тот случай, когда с ходу доверяться результатам Maple 7 рискованно.
В данном случае приходится констатировать давно известный факт — системы компьютерной математики (и Maple 7 в их числе) не всесильны и всегда можно найти интегралы даже с обманчиво простым внешним видом, которые поставят систему в тупик или дадут неверные результаты в той или иной области изменения аргументов. Особенно, опасны интегралы от кусочных функций с разрывами и интегралы, представляемые такими функциями. Именно к ним и относится обсуждаемый сейчас интеграл. Не меньше проблем вызывают интегралы от функций, области определения которых заданы некорректно или просто не изучены.
Между тем ситуация вовсе не является безнадежной. Надо просто знать, что предпринять, чтобы подсказать системе правильный путь решения. Например, в нашем случае, применив параметр continuous (в апострофах), можно получить куда более простое выражение:
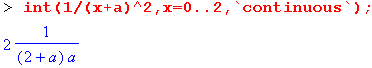

Рис. 8.2. Построение графика зависимости значений интеграла с подынтегральной функцией 1/(х+а)^2 от параметра а
Рисунок 8.3 показывает это решение с двумя важными дополнениями — оно представляется функцией пользователя, а ее график строится при изменении а от -10 до 10.
Приведем еще один пример «каверзного» интеграла довольно простого вида:
> int(l/x^3,x=-1..2);
undefined
Этот интеграл вообще не берется функцией int без указания параметров (в строке вывода сообщается об этом). Но введение параметра CauchyPrinci pal Value позволяет получить значение интеграла:
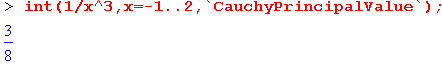
Возьмем еще один наглядный пример — вычисление интеграла от синусоидальной функции при произвольно больших пределах, но кратных 2я! Очевидно, что при этом (учитывая равность площадей положительной и отрицательной полуволн синусоиды) значение интеграла будет равно 0. Например:
> int(sin(x),x-1000*pi..l000*pi);
0
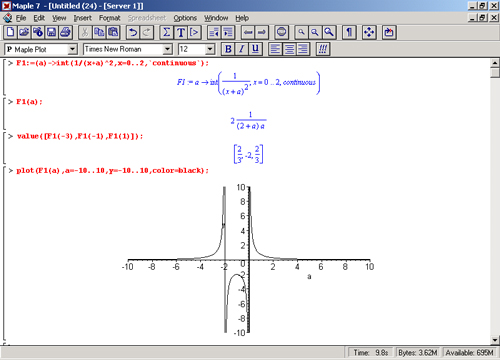
Рис. 8.3. Зависимость значения интеграла с подынтегральной функцией 1/(х+а)^2 и пределами от 0 до 2 от параметра а
Однако распространение этого правила на бесконечные пределы интегрирования является грубейшей ошибкой. Интеграл такого рода уже не берется (или говорят, что он не сходится), и Maple 7 дает соответствующий результат:
> int(sin(x),x=-infinity..infinity);
undefined
Во многих областях техники часто употребляются выражения «затухающая синусоида» или «нарастающая синусоида». Иногда говорят и о «синусоиде с уменьшающейся или возрастающей амплитудой». Бесполезно утверждать, что эти названия принципиально ошибочны — в рамках допущений, принятых в технических расчетах, такие утверждения весьма наглядны и эта, в частных случаях вполне оправданная, наглядность с позиций математики идет в ущерб точности фундаментальных определений.
Возьмем, к примеру, широко распространенную функцию: y(t) = exp(-t)sin(2*Pi*t). Построим ее график и вычислим определенный интеграл от этой функции с пределами от 0 до oo (рис. 8.4).
С первого взгляда на график видно, что Каждая положительная полуволна функции (затухающей «синусоиды») явно больше последующей отрицательной полуволны. К тому же осцилляции функции быстро затухают и через десяток-другой периодов значение функции становится исчезающе малым. Вот почему Maple 7 уверенно вычисляет интеграл с такой подынтегральной функцией. Ее свойство — неопределенность при t->oo исчезает.
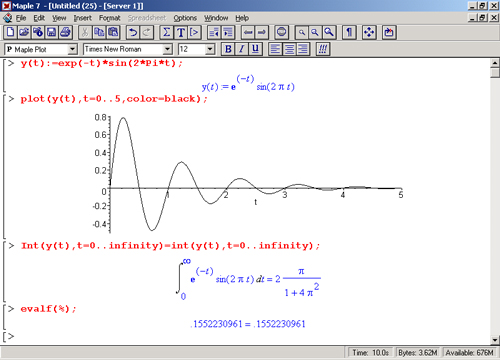
Рис. 8.4. График «затухающей синусоиды» и интеграл от нее с пределами от 0 до oo
Однако называть такую функцию «затухающей синусоидой», безусловно, неточно. Умножение sin(2pt) на множитель, зависящий от времени t, лишает функцию главного свойства синусоиды — ее строгой симметрии. Так что exp(-t)sin(2pt) — это совсем новая функция со своими отличительными свойствами. Главные из них — несимметрия при малых t и исчезающе малые значения при больших t. Ни тем, ни другим свойством обычная синусоида не обладает. А теперь возьмем антипод этой функции — «синусоиду с экспоненциально нарастающей до стационарного значения 1 амплитудой». Такая функция записывается следующим образом:
Y(t) - (1 - exp(-t)) sin(2*Pi*t).
Ее график и попытки вычисления интеграла с такой подынтегральной функцией приведены на рис. 8.5.
Обратите внимание на то, что здесь прямое вычисление интеграла к успеху не привело, хотя из графика функции видно, что каждая положительная полуволна в близкой к t = 0 области явно больше по амплитуде, чем последующая отрицательная полуволна. Однако в отличие от предыдущей функции при больших значениях аргумента данная функция вырождается в обычную синусоиду с неизменной (и равной 1) амплитудой. Вот почему трудяга Maple 7 честно отказывается вычислять интеграл от такой коварной функции.
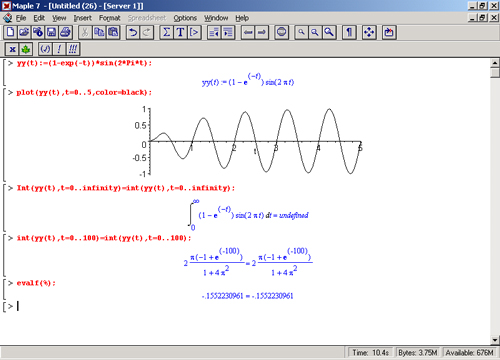
Рис. 8.5. График «экспоненциально нарастающей синусоиды» и интеграл от нее с пределами от 0 до oo
На этом примере очень четко отслеживается разница в мышлении инженера и математика. Инженер скажет, что интеграл с такой функций должен быть, поскольку вначале положительные площади явно меньше отрицательных, а в дальней области они выравниваются, и потому площадь каждого «периода» функции становится примерно нулевой. По-своему инженер прав — если его не интересует точное определение подынтегральной области в заоблачных высотах бесконечности, то мы должны получить то же значение интеграла, что в предшествующем примере, но со знаком «минус». И в самом деле (см. рис. 8.5), интегрируя в пределах от 0 до100п, мы получаем именно это значение (опять-таки в пределах погрешности по умолчанию).
И все же прав здесь математик — переход от интегрирования с конечным (да еще и кратным 2тс) пределом к интегрированию с бесконечным пределом — далеко не простая операция. Она требует учета поведения функции при значении аргумента, стремящегося к бесконечности, а тут говорить о нулевой алгебраической площади синусоиды некорректно, ибо никакой кратности величине 2л у бесконечности нет! Остается лишь радоваться тому, что система Maple 7 может примирить математиков и инженеров, дав им в руки средства, позволяющие решать подобные задачи с приближениями, приемлемыми для тех или иных категорий пользователей.
Мы подробно рассмотрели этот класс задач потому, что многие важные интегральные преобразования (например, преобразование Фурье) оперируют с подобными подынтегральными функциями и надо тщательно разбираться в областях их применения.
ПРИМЕЧАНИЕ
Приведенные выше примеры показывают, что интегрирование является гораздо более тонким делом, чем это кажется на первый взгляд. Тут уместно напомнить, что и студент вуза, и профессор математики университета должны очень внимательно исследовать возможности вычисления интегралов того или иного типа разными математическими системами. Иными словами, применять системы компьютерной математики должны только пользователи, обладающие не столько учеными званиями и степенями, сколько культурой выполнения математических вычислений.
Интегралы с переменными пределами интегрирования
К интересному классу интегралов относятся определенные интегралы с переменными пределами интегрирования. Если обычный определенный интеграл представлен числом (или площадью в геометрической интерпретации), то интегралы с переменными пределами являются функциями этих пределов.
На рис. 8.6 показано два примера задания простых определенных интегралов с переменным верхним пределом (сверху) и обоими пределами интегрирования (снизу).
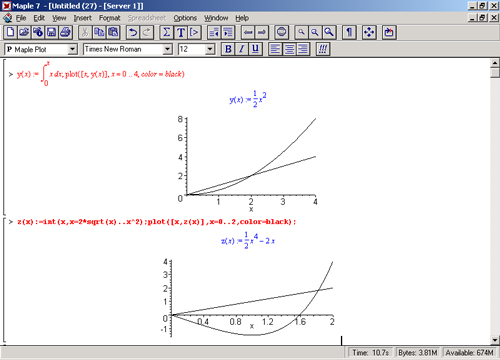
Рис.8.6. Примеры интегралов с переменными пределами интегрирования
На этом рисунке построены также графики подынтегральной функции (это наклонная прямая) и функции, которую задает интеграл.
Функции int и Int могут использоваться для вычисления кратных интегралов, например двойных и тройных. Для этого функции записываются многократно:

Обратите внимание на нечеткую работу функции evalf в последнем примере. Эта функция уверенно выдает значение evalf (Pi) в форме вещественного числа с плавающей точкой, но отказывается вычислить значение интеграла, в которое входит число Pi. Этот пример говорит о том, что отдельные недостатки у Maple 7 все же есть, как и поводы для ее дальнейшего совершенствования.
Описанная возможность вычисления кратных интегралов функциями Int и int не является вполне законной. В пакете расширения student имеются дополнительные функции интегрирования, которые дополняют уже описанные возможности. В частности, в этом пакете есть функции для вычисления двойных и тройных интегралов.
Для вычисления пределов функции f в точке х =а используются следующие функции:
limit(f,x=a); limit(f,x=a.dir);
Limit(f.x=a); Limit(f.x-a.dir);
Здесь f - алгебраическое выражение, х - имя переменной, dir - параметр, указывающий на направление поиска предела (left — слева, right — справа, real — в области вещественных значений, complex — в области комплексных значений). Значением а может быть бесконечность (как положительная, так и отрицательная). Примеры применения этих функций для вычисления пределов в точке приведены ниже:

Обратите внимание на то, что в первом примере фактически дано обозначение предела в самом общем виде. Рисунок 8.7 показывает вычисление пределов функции tan(x) в точке х=n/2, а также слева и справа от нее. Для указания направления используются опции right (справа) и left (слева). Видно, что в самой точке предел не определен (значение undefined), а пределы справа и слева уходят в бесконечность.
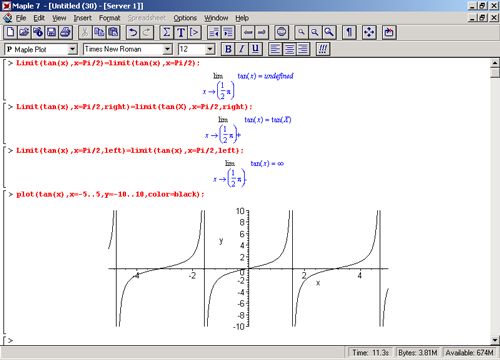
Рис. 8.7. Пример вычисления пределов функции tan(x) и построение ее графика
Показанный на рис. 8.7 график функции tan(x) наглядно подтверждает существование пределов справа и слева от точки х = П/2 и отсутствие их в самой этой точке, где функция испытывает разрыв от значения +oo до -oo.
Огромное разнообразие функций давно заставляло математиков задумываться над возможностями их приближенного, но единообразного представления. К таким представлениям относятся различные ряды, сходящиеся к значениям функций в окрестности заданной точки. Для разложения функции или выражения ехрr в обычный степенной ряд служат функции series(ехрr, eqn) и series(expr, eqn, n). Здесь ехрr — разлагаемое выражение, eqn — условие (например, в виде х=а) или имя переменной (например, х) и n — необязательное и неотрицательное целое число, задающее число членов ряда (при его отсутствии оно по умолчанию берется равным 6, но может переустанавливаться системной переменной Order). Если в качестве eqn задано имя переменной, то это соответствует разложению по этой переменной в области точки с ее нулевым значением. Задав eqn в виде х=х0, можно получить разложение по переменной х в окрестности точки х = х0.
Разложение получается в форме степенного многочлена, коэффициенты которого задаются рациональными числами. Остаточная погрешность задается членом вида 0(х)^n. При точном разложении этот член отсутствует. В общем случае для его удаления можно использовать функцию convert. Ниже представлены примеры разложения различных выражений в ряд:

Здесь видно, что член, обозначающий погрешность, отсутствует в тех разложениях, которые точны, например, в разложениях степенных многочленов. Для визуализации приближения рядами заданных аналитических зависимостей очень полезно построить на одном графике кривые аналитической зависимости и разложения в ряд. Мы это покажем чуть позже на примере ряда Тейлора.
Разложение в ряды Тейлора и Маклорена
Для разложения в ряд Тейлора используется функция taylor(expr, eq/nm, n). Здесь ехрr — разлагаемое в ряд выражение, eq/nm — равенство (в виде х=а) или имя переменной (например, х), n — необязательный параметр, указывающий на порядок разложения и представленный целым положительным числом (при отсутствии указания порядка он по умолчанию принимается равным 6). При задании eq/nm в виде х=а разложение производится относительно точки х =а. При указании eq/nm в виде просто имени переменной разложение ищется в окрестности нулевой точки, то есть фактически вычисляется ряд Маклорена.
Ниже представлены примеры применения функции taylor:
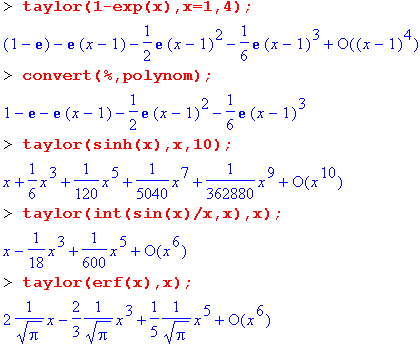
Не все выражения (функции) имеют разложение в ряд Тейлора. Ниже дан пример такого рода:
> taylor(l/x+x^2,x,5):
Error, does not have a taylor expansion, try seriesQ
> series(l/x+x^2,x,10);
je-4*2
> taylor(l/x+x*2,x=l,5);
2 +x - 1 + 2(x - 1f - (x - 1 )3 +(x - 1 )4 +O((x- 1 )5)
Здесь Maple 7 отказалась от вычисления ряда Тейлора в окрестности точки х = 0 (по умолчанию) и предложил воспользоваться функцией series. Однако эта функция просто повторяет исходное разложение. В то же время в окрестности точки х = 1 ряд Тейлора вычисляется.
Для разложения в ряд Тейлора функций нескольких переменных используется библиотечная функция mtaylor:
mtaylor(f. v)
mtaylorCf. v. n)
mtaylor(f. v, n, w)
Здесь f — алгебраическое выражение, v — список имен или равенств, n — необязательное число, задающее порядок разложения, w — необязательный список целых чисел, задающих «вес» каждой из переменных списка v. Эта функция должна вызываться из библиотеки Maple 7 с помощью команды readlib:

Для получения только коэффициента при k=м члене ряда Тейлора можно использовать функцию coeftayl (expr,var,k). Если ехрr — функция нескольких переменных, то k должен задаваться списком порядков коэффициентов.
Пример документа — разложение синуса в ряд
Полезно сочетать разложение выражений (функций) в ряд Тейлора с графической визуализацией такого разложения. Рассмотрим документ, в котором наглядно показаны возможности представления функции рядами Тейлора и Маклорена. На рис. 8.8 показана первая часть документа. Она дает пример разложения в ряд Тейлора функции sin(x) с построением ее графика и графика по разложению в ряд. Поскольку выбрано разложение относительно точки х = 0, то полученный ряд является рядом Маклорена. Это хороший пример визуализации результатов математических вычислений — здесь наглядно видно, что при малых значениях х график ряда практически повторяет разлагаемую функцию, но затем начинает сильно от нее отходить.
Обратите внимание, несмотря на то что мы задали шестой порядок ряда, последний член имеет только пятый порядок. Это связано со спецификой данного разложения — в нем просто отсутствуют члены четного порядка. Можно буквально в считанные секунды попробовать изменить число членов ряда или диапазон изменения переменной х, что и показано на рис. 8.9 (вторая часть документа). При этом легко убедиться в том, что при больших х поведение ряда не имеет ничего общего с поведением разлагаемой в ряд функции, в частности нет и намека на периодичность разложения, которая присуща тригонометрической функции sin(x).
В заключительной (третьей) части этого документа (рис. 8.10) представлено уже истинное разложение синуса в ряд Тейлора в окрестности смещенной от нуля точки х = 1. При смещении точки, относительно которой ведется разложение, выражение для ряда Тейлора существенно изменяется. В нем, во-первых, появляются члены четных степеней, а во-вторых, фигурирует аргумент вида (х- 1)n. Нетрудно заметить, что даже при представлении такой «простой» функции, как sin(x), приемлемая погрешность представления одного периода достигается при числе членов ряда Тейлора порядка 10 и более. Однако существенное повышение порядка ряда нецелесообразно из-за резкого возрастания вычислительных погрешностей. Кроме того, серьезным недостатком аппроксимации рядом Тейлора является непредсказуемое поведение полинома вдали от точки, относительно которой задается представление. Это хорошо видно на всех трех приведенных примерах.

Рис. 8.8. Разложение функции sin(x) в ряд Маклорена 6-го порядка и построение ее графика
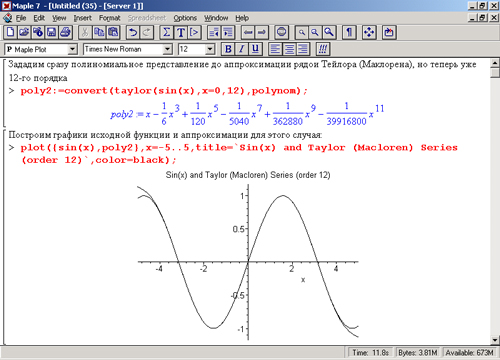
Рис. 8.9. Разложение функции sin(x) в ряд Маклорена 12-го порядка и построение ее графика
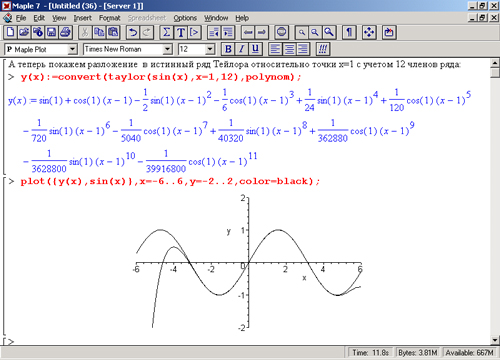
Рис. 8.10. Разложение функции sin(x) в ряд Тейлора 12-го порядка относительно точки х = 1 и построение ее графика
Помимо указанных выше разложений в ряд Maple 7 имеет множество функций для иных разложений. Например, в пакете numapprox имеется функция laurent(expr,var,n), позволяющая получить разложение в ряд Лорана, функция chebyshev(expr, eq/nm, eps) дает разложение в форме полиномов Чебышева и т. д.
Решение уравнений и неравенств
Решение линейных и нелинейных уравнений и неравенств — еще одна важная область математического анализа. Maple 7 имеет мощные средства для такого решения. Так, для решения линейных и нелинейных уравнений в аналитическом виде используется достаточно универсальная и гибкая функция solve(eqn, var) или so1ve({eqnl,eqn2,.. .}.{varl,var2,...}), где eqn — уравнение, содержащее функцию ряда переменных, var — переменная, по которой ищется решение, Если при записи eqn не используются знак равенства или знаки отношения, считается, что solve ищет корни уравнения eqn=0.
Характер решений можно изменить с помощью глобальных переменных:
В решениях могут встречаться следующие обозначения:
В форме solve[subtopic] возможны параметры subtopic функции solve следующих типов:
floats functions identity ineq linear
radical scalar series system
При решении систем уравнений они и список переменных задаются как множества, то есть в фигурных скобках. При этом и результат решения получается в виде множества. Чтобы преобразовать его к обычному решению, нужно использовать функцию assign, которая обеспечивает присваивание переменным значений, взятых из множества.
Функция solve старается дать решение в аналитическом виде. Это не означает, что ее нельзя использовать для получения корней уравнений в численном виде. Просто для этого придется использовать функции evalf или convert. Если результат решения представлен через функцию RootOf, то зачастую можно получить все корни с помощью функции all values.
Решение одиночных нелинейных уравнений
Решение одиночных нелинейных уравнений вида f(x) = 0 легко обеспечивается функций solve(f,(x),x). Это демонстрируют следующие примеры:

Часто бывает удобно представлять уравнение и его решение в виде отдельных объектов, отождествленных с определенной переменной:
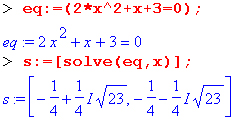
В частности, это позволяет легко проверить решение (даже если оно не одно, как в приведенном примере) подстановкой (subs):

Сводящиеся к одному уравнению равенства вида f1(x)=fl(x) также решаются функцией solve(fl(x)=f2(x),x):

Обратите внимание в этих примерах на эффективность применения функции evalf, позволяющей получить решения, выраженные через функцию RootOf, в явном виде.
Решение тригонометрических уравнений
Функция solve может использоваться для решения тригонометрических уравнений:

Однако из приведенных примеров видно, что при этом найдено только одно (главное) решение. Периодичность тригонометрических функций и связанная с этим множественность решений оказались проигнорированы. Однако можно попытаться найти все периодические решения, выполнив следующую команду:
> _EnvAllSolutions:=true;
EnvAllSolutions := true
Указанная в ней системная переменная отвечает за поиск всех периодических решений, когда ее значение равно true, и дает поиск только главных решений при значении false, принятом по умолчанию. Так что теперь можно получить следующее:

На рис. 8.11 показан более сложный случай решения нелинейного уравнения вида f1(x)=f2(x). где f1(х) = sin(x) и f2(x) = cos(x) - 1. Решение дано в графическом виде и в аналитическом для двух случаев — нахождения главных значений корней и нахождения всех корней.
В решениях встречаются переменные _В1- и _Z1~, означающие ряд натуральных чисел. Благодаря этому через них можно представить периодически повторяющиеся решения.
Примеры решения уравнений с обратными тригонометрическими функциями показаны ниже:
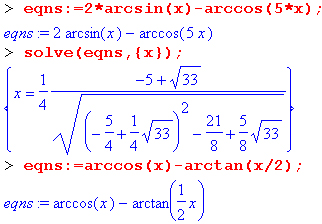
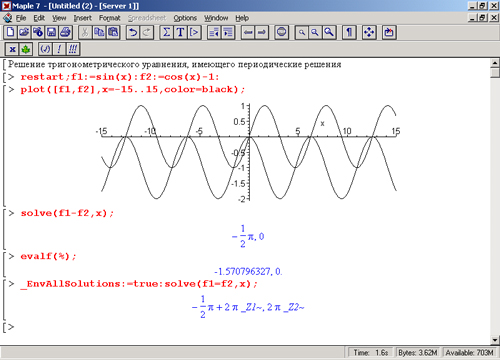
Рис. 8.11. Пример решения уравнения, имеющего периодические решения
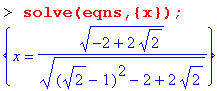
Решение систем линейных уравнений
Для решения систем линейных уравнений созданы мощные матричные методы, которые будут описаны отдельно. Однако функция solve также может с успехом решать системы линейных уравнений. Такое решение в силу простоты записи функции может быть предпочтительным. Для решения система уравнений и перечень неизвестных задаются в виде множеств (см. приведенные ниже примеры).
Рисунок 8.12 дает два примера решения систем из двух линейных уравнений. В первом примере функция solve возвращает решение в виде значений неизвестных х и у, а во втором отказывается это делать.
В чем дело? Оказывается, в том, что во втором случае система просто не имеет решения. Импликативная графика пакета расширения plots дает прекрасную возможность проиллюстрировать решение. Так, нетрудно заметить, что в первом случае геометрическая трактовка решения сводится к нахождению точки пересечения двух прямых, отображающих два уравнения. При этом имеется единственное решение, дающее значения х и у.
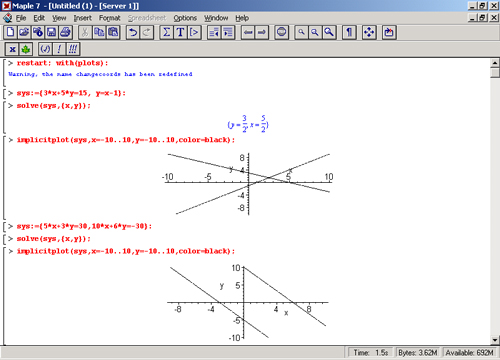
Рис. 8.12. Примеры решения системы из двух линейных уравнений с графической иллюстрацией
Во втором случае решения и впрямь нет, ибо уравнения задают параллельно расположенные прямые, которые никогда не пересекаются. Рекомендуем читателю самостоятельно проверить и третий случай — бесконечного множества решений. Он имеет место, если оба уравнения описывают одну и ту же зависимость и их графики сливаются в одну прямую.
Решение систем из трех линейных уравнений также имеет наглядную геометрическую интерпретацию — в виде точки, в которой пересекаются три плоскости, каждая из которых описывается функцией двух переменных. Для наглядности желательно представить и линии пересечения плоскостей. Это позволяет сделать функция импликативной трехмерной графики tmplicitplotSd, что и показано на рис. 8.13. Для объединения графиков площадей использована функция display.
Некоторые проблемы с решением систем из трех линейных уравнений иллюстрируют примеры, приведенные на рис. 8.14, В первом примере решения вообще нет. График показывает, в чем дело, — линии пересечения плоскостей идут параллельно и нигде не пересекаются. Во втором примере все три плоскости пересекаются по одной линии.
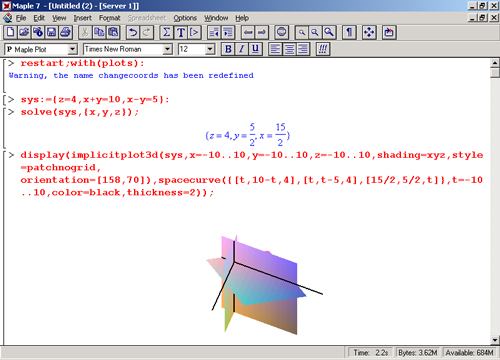
Рис. 8.13. Пример решения системы из трех линейных уравнений с графической иллюстрацией решения
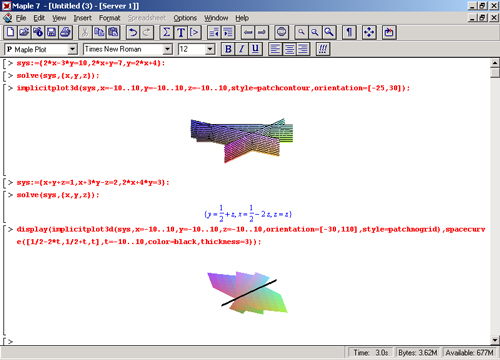
Рис. 8.14. Графическая иллюстрация особых случаев решения системы из трех линейных уравнений
Следующий пример показывает решение системы из четырех линейных уравнений:
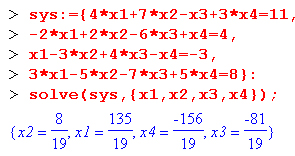
Эта система имеет решение, но его простая графическая иллюстрация уже невозможна.
Случай решения неполной системы уравнений (уравнений — 3, а неизвестных — 4) иллюстрирует следующий пример:
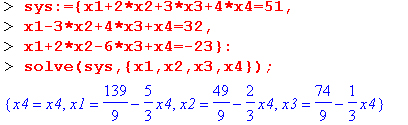
Как видно из приведенных примеров, функция solve неплохо справляется с решением систем линейных уравнений.
Решение систем нелинейных и трансцендентных уравнений
Функция solve может использоваться для решения систем нелинейных и трансцендентных уравнений. Для этого система уравнений и перечень неизвестных задаются в виде множеств. Ниже приведены примеры решения уравнений:

В этих примерах хорошо видна техника работы с функциями solve и assign. В конце примеров показано восстановление неопределенного статуса переменных х и у с помощью функции unassign и снятие определения переменных с помощью заключения их в прямые апострофы.
В решениях уравнений нередко появляется функция RootOf, означающая, что корни нельзя выразить в радикалах. Эта функция применяется и самостоятельно в виде RootOf(ехрr) или RootOf(ехрr, х), где ехрr — алгебраическое выражение или равенство, х — имя переменной, относительно которой ищется решение. Если х не указана, ищется универсальное решение по переменной _Z. Когда ехрr задано не в виде равенства, решается уравнение ехрr=0. Для получения решений вида RootOf в явном виде может использоваться функция all values. Примеры применения функции RootOf:

Итак, функция RootOf является эффективным способом представления решения в компактном виде. Как уже отмечалось, наряду с самостоятельным применением она часто встречается в составе результатов решения нелинейных уравнений.
Решение уравнений со специальными функциями
К важным достоинствам Maple 7 относится возможность решения уравнений, содержащих специальные функции как в записи исходных выражений, так и в результатах решения. Приведем несколько примеров такого рода:

Неравенства в математике встречаются почти столь же часто, как и равенства. Они вводятся знаками отношений, например: > (больше), < (меньше) и т. д. Решение неравенств существенно расширяет возможности функции solve. При этом неравенства задаются так же, как и равенства. Приведенные на рис. 8.15 примеры поясняют технику решения неравенств.
Из приведенных примеров очевидна форма решений — представлены критические значения аргумента, вплоть до не включаемых значений области действия неравенства (они указываются словом Open). Всегда разумным является построение графика выражения, которое задает неравенство, — это позволяет наглядно убедиться в правильности решения. Приведем еще несколько примеров решения неравенств в аналитической форме:

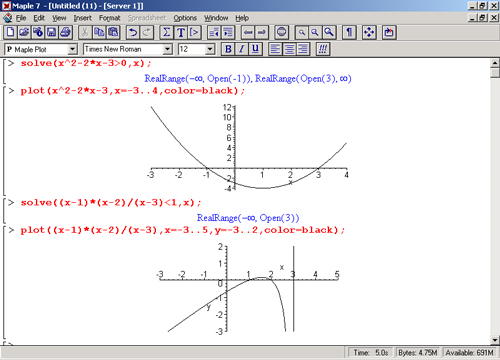
Рис. 8.15. Примеры, иллюстрирующие решение неравенств

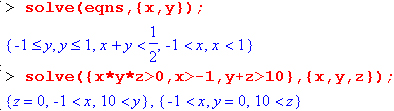
В последних примерах показано решение систем неравенств." При этом выдаются области определения нескольких переменных.
Решение функциональных уравнений
Решение функционального уравнения, содержащего в составе равенства некоторую функцию f(x), заключается в нахождении этой функции. Для этого можно использовать функцию solve, что демонстрируют приведенные ниже примеры:

Решение уравнений с линейными операторами
Maple 7 позволяет решать уравнения с линейными операторами, например с операторами суммирования рядов и дифференцирования. Ограничимся одним примером такого рода:


Решение в численном виде — функция fsolve
Для получения численного решения нелинейного уравнения или системы нелинейных уравнений в форме вещественных чисел удобно использовать функцию:
fsolve( eqns. vars. options )
Эта функция может быть использована со следующими параметрами:
Функция fsolve дает решения сразу в форме вещественных или комплексных чисел, что и показывают следующие примеры:

Заметим, что локализация поиска корней в заданном интервале позволяет отыскивать такие решения, которые не удается получить с помощью функций solve и fsolve в обычном применении. В последнем из приведенных примеров дается решение системы нелинейных уравнений, представленных уравнениями f и д.
Чтобы еще раз показать различие между функциями solve и fsolve, рассмотрим пример решения с их помощью одного и того же уравнения erf(x) = 1/2:
> so1ve(erf(x)=l/2,x);
RootOf(2erf(_Z)-l)
> fsolve(erf(x)=l/2);
.4769362762
Функция solve в этом случае находит нетривиальное решение в комплексной форме через функцию RootOf, тогда как функция fsolve находит обычное приближенное решение.
Решение рекуррентных уравнений — rsolve
Функция solve имеет ряд родственных функций. Одну из таких функций — fsolve — мы рассмотрели выше. В справочной системе Maple 7 можно найти ряд и других функций, например rsolve для решения рекуррентных уравнений, isolve для решения целочисленных уравнений, msolve для решения по модулю m и т. д. Здесь мы рассмотрим решение уравнений важного класса — рекуррентных. Напомним, что это такие уравнения, у которых заданный шаг решения находится по одному или нескольким предшествующим шагам.
Для решения рекуррентных уравнений используется функция rsolve:
rsolve(eqns, fens) ,
rsolve(eqris. fens, 'genfunc'(z))
rsolve(eqns, fens, 'makeproc')
Здесь eqns — одиночное уравнение или система уравнений, fens — функция, имя функции или множество имен функций, z — имя, генерирующее функциональную переменную.
Ниже представлены примеры применения функции rsolve:

А теперь приведем результат вычисления функцией rsolve n-го числа Фибоначчи. Оно задается следующим выражением:
> eql :- (f(n+2) = f(rn-l) + f(n) . f(0) - 1 . f(l) - 1}:
eql~{f(n+2) = f(n + \) + f(n),f(0)=\,f(l)=l}
В нем задана рекуррентная формула для числа Фибоначчи — каждое новое число равно сумме двух предыдущих чисел, причем нулевое и первое числа равны 1. С помощью функции rsolve можно получить поистине ошеломляющий результат:
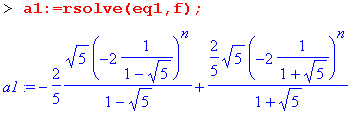
Числа Фибоначчи — целые числа. Поэтому представленный результат выглядит как весьма сомнительный. Но на самом деле он точный и с его помощью можно получить числа Фибоначчи. Ниже показан процесс получения чисел Фибоначчи для n = 5, 7, 10 и 20:
> [normal(subs(n=5,al).expanded).normal(subs(n-7.al).expanded).
normal(subs(n=10,al),expanded),normal(subs(n=20.al),expanded)];
[8,21,89,10946]
Решение уравнений в целочисленном виде — isolve
Иногда бывает нужен результат в форме только целых чисел. Для этого используется функция isolve(eqns, vans), дающая решение в виде целых чисел. Приведем примеры ее применения:
> iso1ve({2*x-5=3*y}):
{x = 4 + 3_Zl,y=\ + 2_Z1]
> iso1ve(yA4-z"2*y*2-3*x*z*y*2-xA3*z);
Во втором из приведенных примеров в выводе появилась вспомогательная переменная %1, которая упрощает запись результата при текстовом формате его вывода (Character Notation). Напоминаем, что в стандартной математической нотации вспомогательная переменная вида %N не формируется. В этом случае упомянутый пример будет выглядеть следующим образом:
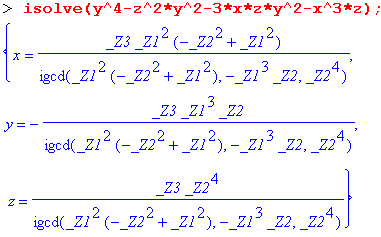
Результат вычислений одинаков при любом формате вывода, но иногда вывод в текстовом формате с выделением вспомогательных переменных имеет преимущество, поскольку выглядит более компактным.
Функция msolve(eqns,vars.m) или msolve(eqns,m) обеспечивает решение вида Z mod m (то есть при подстановке решения левая часть4 при делении нат дает остаток, равный правой части уравнения). При отсутствии решения возвращается объект NULL (пустой список).
Ниже даны примеры использования функции msolve:
> mso1ve({3*x-4*y=l,7*x+y=2}.12);
{у = 5,х=3}
> msolve(2^i=3.19);
{(=13 + 18_Z7~}
> mso1ve(8*j-2,x,17);
{/ = 3 + 8*}
На этом мы завершаем рассмотрение функций для решения уравнений, неравенств и систем с ними.
В этом уроке мы научились:
|
|