 (21)
(21)
При анализе монохромного изображения при использовании преобразования Радона, как описано ранее, исходное изображение отображается в некоторое пространство признаков (так для (k,b) – преобразования это пространство параметров прямой k и b, а для нормального – ρ и θ соответственно). Затем по виду результирующего изображения можно судить о наличии на исходном изображении определённых объектов, их формы и т.д. Как отмечалось ранее, при реализации такого преобразования появляются определённые сложности, связанные с необходимостью “подгонять” значения аргументов под рассматриваемые параметры. Такой необходимости не будет, если анализировать не исходное изображение, а результирующее пространство. Каждой точке его можно поставить в соответствие счётчик, и затем, анализируя результаты аналогичного преобразования наращивать счётчики. Таким образом, анализируя счётчик каждой точки результирующего пространства, представляющей собой ни что иное, как представление фигуры интереса (искомой фигуры, кривой и т.д.), можно судить о наличие фигур с задаваемыми параметрами.
Такое преобразование называется преобразованием Хафа. Его идея состоит в выявлении кривых заданных определёнными параметрами:
 (21)
(21)
Пространство, содержащее результирующее изображение называют фазовым. Его образуют параметры семейства кривых а1,а2,...an, задаваемого формулой (19).
Алгоритм поиска заданных прямых очень прост и состоит лишь в вычислении значений счётчиков фазового пространства, а затем, в поиске наибольших их значений.
Существует несколько модификаций вычисления преобразования Хафа.
Преобразование Хафа может применяться там, где необходимо анализировать формы кривых. Это всевозможные системы распознавания образов, таких как рукописный шрифт, анализ изображений микросхем, аэрокосмических снимков а также системы слежения (рис. 10).
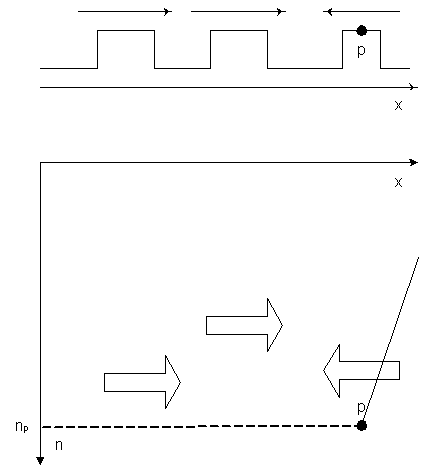
Пусть х – одномерная последовательность, полученная после предварительной обработки видео изображения. Значение n определяет номер кадра. Траектория движения точки p – некоторая кривая.
Если движение точки равномерно, то кривая есть прямая линия, задаваемая уравнением:
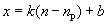 (22)
(22)
Таким образом, пространственно-временное преобразование, описанное в [5], построенное на основании принципов преобразования Хафа было применено в системе слежения.
|
|