Проблема использования оптического излучения для диагностики внутренних органов всегда привлекала исследователей. Основная причина – безвредность оптического излучения для человека. Не мало важную роль играют и относительная дешевизна источников и приемников оптического диапазона, особенно по сравнению с рентгеновскими или ЯМР системами. Множество экспериментальных фактов указывало на возможность применения оптического излучения для просвечивания биотканей. Нетрудно самостоятельно убедиться в том, что кожа и подкожные ткани частично прозрачны для излучения в видимом и ближнем ИК-диапазонах. Поэтому был проявлен интерес к установлению того факта, можно ли по наблюдаемой картине, полученной в результате диафаноскопии (просвечивания) не слишком толстых биологических тканей указать на патологию, и существует много очевидных доказательств в поддержку этой развивающейся области диагностики. Метод найдет применение при обследованиях молочной железы, а также в дифференциальной диагностике кистозных (доброкачественных) поражений и злокачественных опухолей. Кисты (заполненные жидкостью) видны как области с повышенной яркостью, если жидкость, заполняющая их, не является кровью, в то время как затемненные области в диафаноскопическом изображении с большой вероятностью указывают на наличие злокачественной опухоли. Фиброаденомы дают изображение, окрашенное в интенсивный вишнево-красный цвет. Аналогично проводится дифференциальная диагностика плотных злокачественных опухолей и кист при заболеваниях мошонки. Еще одной потенциальной областью применения метода является исследование головного мозга новорожденного.
Однако роль метода диафанографии в диагностике молочной железы вызывает сомнение, и его необходимо сопоставить с такими конкурирующими методами, как маммография, ультразвуковая диагностика и биопсия. Диафанография с хорошим качеством аппаратуры представляет собой новейший метод, апробированный пока лишь в нескольких центрах, и то в различном техническом исполнении, и, хотя он является многообещающим методом, общепринятая точка зрения в его пользу до сих пор не сложилась. Однако для определенности следует заметить, что существует относительно немного работ, посвященных сравнению этого метода с другими методами диагностики, причем даже полученные выводы неоднозначны. Основным аргументом против рентгеновской маммографии как метода скрининга является опасность накопления большой дозы облучения, и в этом отношении диафанография представляет собой альтернативный метод, безвредный для пациента. Однако низкое пространственное разрешение диафаноскопической визуализации делает этот метод слабым конкурентом, если целью клинического обследования является определение микроструктурных образований у пациентов, заболевание которых протекает бессимптомно. Тем не менее при массовом скрининге выявляют 10% опухолей, возникающих в течение года после проведения маммографии и получения отрицательных показаний (эти опухоли называют интервальными); в этом отношении диафанография предлагает полезное дополнение к индивидуальному мониторингу методом пальпации или более рискованной маммографии, увеличивая выявляемость при массовых обследованиях. Если при просвечивании обнаруживается какая-либо аномалия, то пациента можно обследовать методом маммографии или сделать биопсию для подтверждения диагноза. В случае обследования плотной груди у молодых женщин маммографии присущи свои ограничения, что является еще одним стимулом к развитию диафанографии. К сожалению, (неизбежные) сравнения возможностей методов визуализации обычно проводятся на пациентах, уже имеющих признаки или симптомы заболевания, и в этом смысле они не позволяют оценить относительную эффективность методов при массовых обследованиях. Не следует также игнорировать тот факт, что при опросе 95% женщин отдали предпочтение диафанографии, если имелась необходимость в последующих обследованиях.
Необходимо также напомнить, что физические основы метода диафанографии в значительной степени отличаются от конкурирующих с ней методов диагностики, поскольку диафанография позволяет получать информацию о различных свойствах биотканей, важная роль которых до конца еще не установлена. Таким образом, целесообразно продолжить разработку этого метода, а также изучение биологических механизмов поглощения, затухания и рассеяния излучения в видимом и ИК-диапазонах.
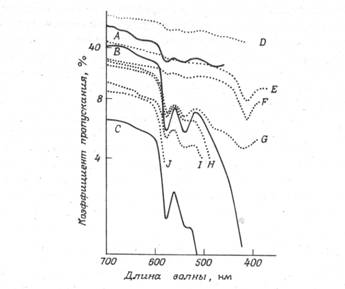
Коэффициент пропускания света биотканями зависит от длины волны излучения, вида просвечиваемой биоткани и ее толщины. Надежные данные об оптических характеристиках биоткани практически отсутствуют. Известно, что щека толщиной

кривые А — С относятся к злокачественным новообразованиям; кривая Е — к свиному жиру; кривая О — к ткани молочной железы в норме; все остальные кривые относятся к фиброаденомам. Препараты имели различные толщины: А —5 мм, В —
Рисунок 7.1. Кривые пропускания для образцов биоткани молочной железы, удаленных в ходе хирургической операции:
Цвета в изображении зависят также и от спектра падающего света. В естественных условиях множество красных кровяных телец можно рассматривать как систему фильтров. Кроме того, в экспериментах предполагается, что удельное содержание эритроцитов в нормальных тканях молочной железы составляет около
Основным показателем при диафанографии молочной железы является дифференциальная прозрачность ее тканей для света, поэтому была разработана математическая модель взаимодействия электромагнитной волны с биосредой. В биоткани свет может как по-' глощаться, так и рассеиваться, что приводит к диффузному пропусканию. Рассеяние обусловлено вариациями показателя преломления в микроскопических и макроскопических областях, тогда как поглощение — электронными переходами и возбуждением, связанными с колебательными и вращательными процессами в атоме. При этом закон Бера
![]() (7.1)
(7.1)
связывающий интенсивность падающего света I0 с интенсивностью прошедшего света I, коэффициентом поглощения mа и толщиной просвечиваемого слоя х и справедливый для прозрачных сред, в данном случае непригоден и должен быть заменен решением стационарного уравнения диффузии
![]() (7.2)
(7.2)
где,
D—коэффициент диффузии:
![]() (7.3)
(7.3)
Здесь w — среднее значение косинуса угла рассеяния, a ms — коэффициент рассеяния. Для изотропного рассеяния (w = 0), которое предполагается в тканях молочной железы (см. разд. 7.3), решение уравнения (7.1) записывается в виде
![]()
где

Величина L называется диффузионной длиной или глубиной проникновения. Другая модель, известная как модель Кубелки — Мунка, приводит к весьма похожему заключению о том, что интенсивность проходящего через биоткань света описывается простым экспоненциальным законом, причем скорость поглощения определяется значениями коэффициентов поглощения и рассеяния. Эти коэффициенты были экспериментально измерены для тканей молочной железы и использовались для модельных расчетов контраста в диафанографии. Заметим, что ms = 0 выражение (7.3) с точностью до постоянных переходит в закон Бера, иллюстрируя аналогию с законами затухания рентгеновского излучения.
Наконец, метод просвечивания органов излучением в ближней ИК-области был применен в другом контексте, а именно для степени насыщения кислородом головного мозга и мышц у новорожденных. Гипоксия клеток головного мозга у новорожденных является основной причиной задержки развития нервной системы, особенно у недоношенных детей. Была разработана аппаратура для получения на просвет цифровых изображений на длине волны 658 ± 50 нм, что бы продемонстрировано снимками головы и кисти руки. Было уставлено, что для просвечиваемых тканей толщиной больше нескольких сантиметров разрешение может быть низким, однако с помощью метода обращения свертки качество изображения можно повысить.
Очевидно, что метод диафанографии должен занять свое место в визуализации, однако его значимость по сравнению с другими методами получения изображения в настоящее время еще не определена. В речение последующих нескольких лет его роль могла бы быть уточнена.
На указанных принципах была предложена система компьютерной томографической диафанографии, разработанная с целью повышения контраста изображения. Сконструирован механизм, с помощью которого оптические источник и компьютер способны вращаться в диапазоне углов 180° (127 дискретных положений), а также линейно перемещаться на расстояние
При исследовании процесса распространения света в рассеивающих случайно-неоднородных средах решают, как правило, две основные задачи. Первая связана с определением оптических свойств среды по результатам измерения рассеянного поля определенной структуры. Вторая – с определением структуры светового поля, проникающего в рассеивающую среду при известных ее оптических свойствах. Эти задачи решаются, как правило, с использованием спектрометрических методов, при этом определяются либо интегральные характеристики, либо свойства искомой величины в малом объеме.
Представляет интерес использование томографических методов, позволяющих получать значения искомой величины в сечении исследуемого объема для решения задач диагностики сред и оптического излучения. В рассмотренных ранее схемах при томографическом анализе объект зондировался коллимированным пучком с различных направлений, и регистрировалась прошедшая часть излучения. Эти данные служили исходными для последующей обработки, заключающейся в решении обратной задачи, которая описывается интегральным уравнением Радона. Такие многоракурсные схемы использовались для измерения локальных значений коэффициента поглощения внутри исследуемого объекта. В них регистрировалось и обрабатывалось лишь прошедшее излучение; рассеянным же светом либо пренебрегали, либо его отфильтровывали.
В настоящем разделе предлагается проводить анализ неоднородных сред и световых полей по излучению, рассеянному средой. Возможность проведения таких исследований рассматривается в настоящее время рядом авторов. Например, в работах новосибирских ученых задача ставится в общем случае, когда трехмерный объект зондируется со всех сторон излучением с заданными характеристиками и задано распределение интенсивности рассеянного поля на границах объекта. При этом в общем случае доказывается единственность и существование решения обратной задачи.
При анализе возможности восстановления внутренней структуры объекта по рассеянному им излучению для конкретной схемы исследования необходимо решить следующие задачи: 1) выбрать модель среды, отвечающую заданным физическим характеристикам объекта; 2) записать уравнение распространения излучения в среде для выбранной модели среды при заданной схеме зондирования; 3) определить уравнение, связывающее измеряемые параметры рассеянного излучения с исследуемыми характеристиками среды, т. е. получить основное интегральное уравнение; 4) получить формулу обращения или выбрать алгоритм решения интегрального уравнения; 5) определить условия, при которых регистрация рассеянного излучения позволит получить полный набор данных, необходимый для решения интегрального уравнения. Решение последней задачи позволит сформулировать основные требования к схеме зондирования и регистрации рассеянного излучения.
При исследовании возможности восстановления структуры объекта по рассеянному излучению наибольший интерес представляет схема (рисунок 7.2), в которой объект освещается только одним пучком, направленным вдоль оси z, и для последующей обработки используется излучение, рассеянное в плоскости ху (перпендикулярной к падающему пучку) и регистрируемое с различных направлений.
Ниже мы рассмотрим решение указанных задач для различных моделей среды и сформулируем условия, при которых для заданной схемы зондирования возможно восстановление либо внутренней структуры рассеивающей среды (распределение коэффициента экстинкции), либо распределение интенсивности в сечении потока проникающего излучения.
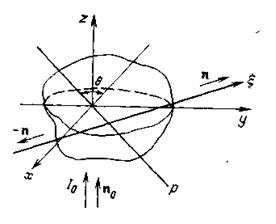
Рисунок 7.2. Схема зондирования объекта
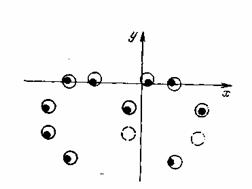
Рисунок 7.3 Восстановленное изображение
рассеивающих частиц
Для описания процесса распространения света в случайно-неоднородной среде воспользуемся уравнением переноса излучения. Рассмотрим два варианта рассеивающих сред с малой плотностью частиц. В качестве первой модели выберем среду, представляющую собой набор дискретных рассеивателей, что достаточно часто встречается на практике. Такими средами являются, например, двухфазные потоки, частицы в газах и жидкостях и т. п. Если концентрация рассеивателей в исследуемом объеме достаточно мала, то поле издающего излучения, рассеянного какой-либо неоднородностью, не испытывает практически вторичного рассеяния на других неоднородностях в любом направлении. Данный случай соответствует однократному рассеянию без учета затухания рассеянной волны. Легко показать, что плотность рассеивателей приближается к плотности идеального газа, при этом относительные флуктуации параметров среды могут быть достаточно велики. В этом случае уравнение переноса излучения имеет очень простой вид:
![]() (7.4)
(7.4)
где
I0(ξ,n0) – интенсивность падающего поля в направлении n0;
I(ξ,n) –интенсивность поля, рассеянного в направлении n;
σ1(ξ) – дифференциальное сечение рассеяния при n-n0=π/2;
σ0(ξ) – полное сечение рассеяния или коэффициент экстинкции.
Решение простого линейного дифференциального уравнения (7.4) имеет вид:
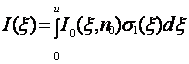 (7.5)
(7.5)
где
0,u – граничные точки сечения.
Учитывая, что выражение (7.5) представляет собой интегрирование искомой функции вдоль прямой ξ, можно представить интенсивность рассеянного поля в каждой точке на регистраторе в виде преобразования Радона от функции Io(x,y)σ1(x,y):
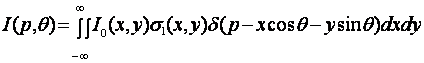 (7.6)
(7.6)
Регистрируя рассеянное поле под различными углами в плоскости, перпендикулярной к направлению зондирующего пучка, можно набрать полный набор данных, необходимый для восстановления значений I0σ1. При условии зондирования исследуемого сечения полем с известным распределением интенсивности в сечении I0(х,у) нетрудно определить дифференциальное сечение рассеяния σ1(х,у).
С целью проверки возможности томографических измерений двухфазных сред были проведены модельные эксперименты. Тест-объектом служили 10 рассеивающих центров, расположенные в одной плоскости. Они освещались лазерным пучком, перпендикулярным к плоскости рассеивателей. Для выделения составляющей, перпендикулярной к регистратору, использовалась система оптической фильтрации. Восстановление производилось по упрощенному алгоритму обратных проекций. Обратное проецирование выполнялось последовательно, что позволило легко исключить ошибки измерений. Этот алгоритм может быть легко реализован в оптоэлектронном процессоре. На рисунке 7.3 представлено изображение, полученное по 12 проекциям (из 18 измеренных). Черные точки – истинное расположение рассеивателей, сплошные окружности–восстановленное изображение, штриховые – артефакты, в которых пересеклись 6 проекций. Как показали проведенные эксперименты, алгоритм обратного проецирования позволяет получать координаты рассеивателей достаточно точно. Артефакты, которые возникают при этом, обусловлены малым числом проекций, существенно меньшим по величине (в нашем случае –
В качестве второй модели рассеивающей среды выберем такую,
в которой параметры среды представляют собой непрерывную функцию с малой дисперсией флуктуации в исследуемом сечении объекта. При этом мы по-прежнему будем считать рассеяние однократным, но будем учитывать затухание рассеянной волны вдоль пути распространения. Такое приближение называется первым приближением многократного рассеяния. В этом случае изменение интенсивности рассеянного поля в направлении n (рисунок 7.2), вызванное неоднородностями, лежащими на оси ξ, будет обусловлено двумя факторами: приростом интенсивности за счет рассеяния в направлении n первоначального поля и ослаблением интенсивности за счет рассеяния при распространении вдоль оси во все направления. В силу приближения однократного рассеяния излучением, пришедшим от других неоднородностей, не лежащих на выделенной оси наблюдения ξ, можно пренебречь. Тогда уравнение переноса излучения запишется в виде:
![]()
![]() (7.7)
(7.7)
Решение данного линейного дифференциального уравнения ищется в виде:![]()
![]()
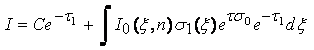
где
С - определяется с помощью подстановки в уравнение граничных условий. Граничные условия в нашей задаче таковы, что интенсивность рассеянного поля в точке ξ = 0 равна I(0)=I0(0). Поэтому мы получаем значение С = 0. В этом случае решение (7.7) запишется в виде:
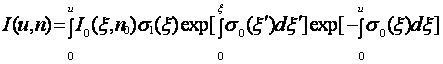 (7.8)
(7.8)
где
0 и u – граничные точки сечения.
Для определения коэффициента экстинкции рассеивающих сред в исследуемом сечении ху будем использовать излучение с известным распределением интенсивности в этом сечении Io(ξ). Предположим также, что индикатриса рассеяния f1=σ1(σ)/σ0(σ) известна и обладает свойством однородности, т. е. f1 = const для каждой точки среды.
Заметим, что в выражении (7.8) присутствует интеграл с переменным верхним пределом от искомой функции σ0(х,у), поэтому решение интегрального уравнения относительно σ0 невозможно. Покажем, что оптические свойства среды можно определить, выбирая в качестве исходных данных интенсивность поля, рассеянного в противоположных направлениях (n и -n), т. с. используя сумму:
![]()
![]()
Выражение для I(0,-n), также полученное решением уравнения переноса излучения, имеет вид, аналогичный выражению (7.8):
 (7.9)
(7.9)
Тогда
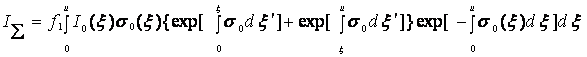 (7.10)
(7.10)
При дальнейшем анализе предположим, что при распространении поля в исследуемой среде учитывается только однократное рассеяние и затухание поля невелико, т. е.
 (7.11)
(7.11)
Раскладывая сумму экспонент в выражении (7.10) в ряд, после несложных преобразований получаем:
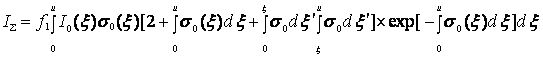 (7.12)
(7.12)
Считая, что интенсивность зондирующего излучения постоянна в плоскости ху, т. е. Io = const, и вспоминая условие f1 = const, получаем:
![]() (7.13)
(7.13)
Предположим, что член R2/4 равен по величине погрешности измерений IΣ, которая, как правило, при томографических измерениях составляет около 5%, т. е. R2/4≤0,5(2+R). Максимально допустимое значение R в этом случае будет равно 0,7. Полагая, что затухание в среде не превышает найденного значения, что справедливо для широкого класса объектов, переписываем уравнение (7.12) при условии I0 = const в виде:
![]() (7.14)
(7.14)
Таким образом, измеренная величина IΣ представляет собой не которую функцию от интеграла искомого распределения σ0(x,y) по выбранной прямой наблюдения ξ. Учитывая это, перейдем к нормальной записи луча наблюдения xcosθ+ysinθ = p и перепишем уравнение (7.14) в виде:
![]() (7.15)
(7.15)
где
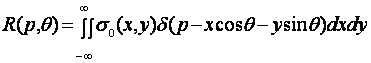 (7.16)
(7.16)
—преобразование Радона функции σ0(х,у).
Следовательно, измеренные проекции IΣ(p,θ) связаны с преобразованием Радона коэффициента экстинкции σ0(х,у) нелинейным уравнением (7.15). Функция (2R+R2)e-R является двузначной; однако в нашем случае двузначность исчезает, так как при R≤21/2 функция (2R + R2)e-R монотонно возрастающая. Решая (7.15) относительно преобразования Радона R(p,θ) для каждой пары (p,θ), можно затем восстановить σ0(х,у) с помощью алгоритмов вычислительной томографии.
Таким образом, измеряя в диапазоне углов 0≤θ<2π суммарную интенсивность поля, которое рассеяно в плоскости, перпендикулярной к падающему полю, мы получаем набор данных, необходимый для решения обратной задачи, т. е. для определения оптических свойств среды. Рассмотренные частные случаи имеют в первую очередь методическую ценность, т.к. показывают принципы решения задач томографии рассеивающих сред, но, к сожалению, не позволяют решить задачу в общем случае.
В настоящее время медико-биологические приложения оптической томографии достаточно бурно развиваются в самых различных направлениях. Она используется не только для исследования макрообъектов -, но и для изучения объектов на микро- уровне. Так называемая микротомография является современным перспективным направлением в микроскопии, открывающим потенциально новые возможности исследования внутренней структуры микрообъектов. Прежде чем подробно остановиться на схемах оптических микротомографов рассмотрим два вопроса, во-первых,основы взаимодействия оптического излучения с биологическим микрообъектом, и, во-вторых, основы построения современных микроскопов.
Задача микроскопии на современном этапе - измерение параметров микрообъектов вообще и живой клетки в частности. При этом не только морфометрических параметров, но и характеристик отражающих ее жизнедеятельность. Взаимодействие оптического излучения с живой клеткой и формирование в оптическом микроскопе ее изображения имеет некоторые особенности, которые мы рассмотрим в данном разделе.
Оптическое излучение, которое используется в микроскопии в качестве зондирующего, представляет собой электромагнитное поле в диапазоне длин волн от 0.4 мкм (синий свет) до 0.8 мкм (красный свет). Данное поле имеет несколько характеристик, изменяющихся при прохождении через микрообъект.
Две основные характеристики - амплитуда и фаза поля описывают пространственно-временное распределение поля. Как правило они обозначаются А(x,y), j(x,y).
До объекта расположенного в предметной плоскости x, y, распределение амплитуды и фазы поля в микроскопии считается постоянным. A(x,y)=const, j(x,y)=const.После объекта происходит модуляция этих составляющих поля A(x,y)=var, j(x,y)=var.
Собственно изменения в амплитуде и фазе поля и несут информацию о клетке. Задача микроскопа донести эту модуляцию поля до глаза человека при визуальном наблюдении или до регистратора с минимальными искажениями. Этот процесс носит название формирование изображения микрообъекта.
Необходимо отметить, что в оптике возможна регистрация только интенсивности света, которая пропорциональна квадрату амплитуды поля I(x,y)=A(x,y)2. Поэтому в различных типах микроскопов происходит преобразование амплитуды и фазы, если есть необходимость визуализировать другие составляющие поля. Об этом будет рассказано позднее на конкретных примерах.
Существует еще одна характеристика электромагнитного излучения - поляризация, которая связана с векторным характером поля и определяет направление электромагнитных колебаний в пространстве. Этот параметр достаточно широко используется в поляризационной микроскопии биообъектов и он также визуализируется при помощи специальной приставки к микроскопу.
В последнее время при анализе тканей и клеток начала применятся такая характеристика поля, как когерентность. Данный параметр используется в интерференционной микроскопии. Это вызвано тем, что в биологии и медицинской практике стали применяться лазеры, излучение которых обладает высокой степенью когерентности. Не вдаваясь в детали можно сказать, что когерентность определяет взаимную согласованность электромагнитных колебаний (света) во времени и разных точках пространства.
Рассмотрим живую клетку, как чисто физический объект и определим каким образов вещество, из которого она состоит, взаимодействует с оптическим излучением.
Каждому веществу, в том числе и составляющему клетку, присущи две характеристики, определяющие его взаимодействие со светом, - коэффициент (показатель) поглощения К и показатель преломления n. Обе они зависят от плотности вещества, но описывают различные виды взаимодействия оптического излучения с веществом. Поглощение света представляет собой уменьшение его интенсивности при прохождении через среду за счет взаимодействия с ней. Показатель поглощения величина обратная расстоянию, которое прошел свет через среду. Из определения видно, что процесс поглощения приводит к изменению (модуляции) амплитуды света.
Преломление света представляет собой явление, при котором уменьшается скорость распространения излучения в среде, относительно скорости света в вакууме. В разных веществах скорость распространения света, естественно, различна. Показатель преломления есть отношение скоростей распространения света в двух различных средах n= V1/V2, где V1 и V2 есть скорости распространения света в двух различных средах. Как правило, в качестве одной из сред используют вакуум и рассматривают показатель преломления относительно вакуума, т.н. абсолютный показатель преломления n=C/V, здесь С - скорость света в вакууме.
Практически измеряют скорость света в воздухе. Величина показателя преломления безразмерная, т.к. скорость света в среде всегда меньше скорости в вакууме, то показатель преломления всегда больше единицы. Этот процесс также обусловлен взаимодействием оптического излучения со средой. Однако, свет при этом не ослабевает, т.е. нет модуляции амплитуды, а изменяется фаза света. На границе раздела двух сред свет изменяет направление распространения - преломляется. Угол преломления зависит от угла падения света на границу раздела двух сред. При нормальном падении - свет не изменяет направление распространения. В следующем разделе мы подробно рассмотрим процесс преломления света.
Существует еще одно свойство некоторых органических веществ, которое получило название оптическая активность. Суть его заключается в том, что при прохождении света через них изменяется (вращается) его поляризация. Угол поворота вектора поляризации зависит от концентрации вещества. К таким органическим веществам относятся, в частности, растворы сахарозы и глюкозы, а также растворы всех без исключения белков. Поэтому это явление используется для измерения их концентрации.
Поляризация света изменяется также и в веществах обладающих свойством двойного лучепреломления. Когда пучок плоскополяризованного света распространяется в такой среде, то, как правило, он разлагается на два луча, которые поляризованы во взаимно перпендикулярных плоскостях. Показатель преломления у таких веществ зависит от поляризации света. Один из лучей называется обыкновенным. Он проходит через объект, подчиняясь обычному закону преломления. Другой – необыкновенный, распространяется в среде с другой скоростью. Различия между этими двумя лучами на выходе из объекта позволяет судить о свойствах вещества. К биологическим объектам, обладающим этим свойством, относятся, в частности, клетки мышечных волокон.
Перечисленные свойства присущи, как однородным, так и неоднородным веществам. Очевидно, что клетка представляет собой пространственно неоднородную структуру с переменной плотностью. Такими неоднородностями служат мембраны клетки и ее органел и сами органелы, находящиеся внутри клетки. Плотность различных органел клетки изменяется в достаточно широких пределах и, следовательно, достаточно сильно изменяются ее оптические свойства. Оптическое излучение в однородной среде распространяется прямолинейно. Это приближение носит название геометрической оптики. В неоднородной среде свет при распространении начинает отклоняться от прямолинейного распространения.
Необходимо выделить два разных случая.
1.Если оптическая неоднородность не сильно отличается по плотности от окружающей среды и изменения плотности происходят плавно, то мы можем считать, что свет продолжает распространяться по лучу, который может при этом отклониться от прямолинейной траектории. Это явление получило название рефракции света. В нашем случае это соответствует распространению излучения внутри цитоплазмы, ядра и других органел, размер которых превышает 1-2 микрона.
2. В том случае, когда однородность меньше микрона или границы ее резкие наблюдается такое явление, как дифракция света на оптических неоднородностях. Причем чем больше неоднородность отличается по плотности от окружающей среды, тем существеннее дифракционные эффекты. На резких границах отклонение очень существенное. Дифракция света тесно переплетается с явлениями рассеяния света в неоднородных средах. Поэтому часто в литературе эти эффекты не различают. В клетке таким структурам соответствуют в первую очередь мембраны, а также мелкие (меньше микрона) включения.
Для наглядности на рисунке 7.4 схематично представлено распространение оптического излучения через клетку.
Все рассмотренные виды взаимодействия света с веществом не изменяли длины волны излучения, выходящего из объекта. Однако в микроскопии широко применяется такое явление как люминесценция или флуоресценция. Суть его заключается в достаточно длительном собственном свечении объекта. Оно может быть вызвано двумя различными механизмами. Во-первых, природа вещества, составляющего клетку или внедренного в нее такова, что обладает способностью к собственному свечению. Но этот эффект наблюдается довольно редко. Во-вторых, свечение вещества внутри клетки под действием внешнего излучения. При этом длина волны вторичного излучения, как правило, больше внешнего. Направление распространения собственного излучения произвольно. На рисунке данный вид взаимодействия света с веществом клетки иллюстрируется лучом 1.
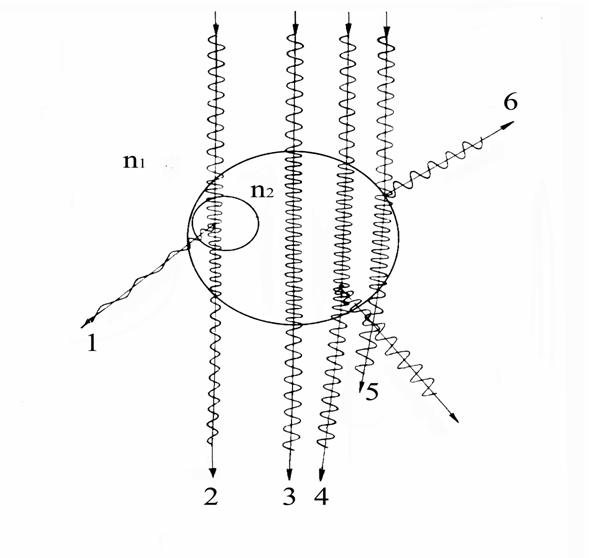
1 - люминесценция
2 – поглощение
3 – идеальный случай
4 – рассеяние
5 – преломление
6 - отражение
Рисунок 7.4 - Схематическое изображение преломления, рассеяния, поглощения и отражения лучей при их прохождении через микроскопический биологический объект
Прежде, чем перейти к ключевому вопросу микроскопии - процессу формирования изображения живой клетки, мы должны определить физическую модель объекта, т.е. его оптические и геометрические параметры.
Морфологические характеристики самых различных клеток изучены очень хорошо и подробно описаны в литературе. Как известно, они отличаются довольно широкой вариабельностью размеров и форм. Для определенности выберем клетки крови, так как в дальнейшем именно на них мы будем проводить большинство измерений.
 |
Рисунок 7.5.
Представим клетку в виде эллипсоида размером 8х15х15 мкм. Размеры различных органел клетки известны также достаточно и некоторые из них приведены в таблице 7.1.
Живая клетка, с точки зрения оптики, представляет собой трехмерное распределение вещества с переменной плотностью, окруженное достаточно плотной оболочкой.
Как уже указывалось вещество, составляющее клетку характеризуется двумя физическими величинами- показатели поглощения и преломления.
Известно, что в видимой области спектра живые одиночные клетки практически не поглощают излучения. В отдельных случаях, когда они содержат пигментные зерна, хлорофилл или иные подобного типа вещества возможно наблюдение заметного эффекта поглощения. Именно поэтому в микрофотоцитометрии используют специальные красители для исследования количественных характеристик концентрации вещества внутри клетки по показателю поглощения. Избирательное поглощение существует только в ультрафиолетовой и инфракрасной областях спектра, которые не визуализируются в световом микроскопе. В этой связи мы при дальнейшем анализе прохождения оптического излучения через клетку можем не учитывать поглощения клетки.
Таблица 7.1
| поз. |
название |
форма и размеры (усредненные) |
плотность, г/см3 |
Dn |
| 1 |
цитоплазма |
0,06 |
0,011 |
|
| 2 |
ядро |
эллипсоид, 5х8х8 мкм |
0,1 |
0,018 |
| 3 |
ядрышко |
шар, диаметр 1 мкм |
0,16¸0,19 |
0,029¸ 0,034 |
| 4 |
митохондрии |
нити. толщина 0,5 мкм |
0,09¸0,11 |
0,0016¸ 0,020 |
| 5 |
гранулы |
шары, диаметр 0,5¸1 мкм |
0,12 |
0,022 |
Таким образом, основной физической величиной, определяющей прохождение оптического излучения через клетку, является показатель преломления, значения которого изменяются внутри клетки в существенных пределах. Напомним, что в таких объектах изменяется только фаза света, поэтому они получили название фазовых объектов. В дальнейшем понятие показателя преломления будет очень широко использоваться в нашей книге, поэтому остановимся подробнее на этой ключевой для нас физической характеристике вещества.
Раздел оптики изучающий свойства показателя преломления различных веществ называется рефрактометрией, Это понятие ввел в науку еще Ньютон в своем трактате "Оптика". Он же установил связь между показателем преломления и плотностью вещества. Эта эмпирическая формула многократно уточнялась различными исследователями. Для нашей задачи-рефрактометрии живых клеток, представляющих собой некоторый раствор, больше всего подходит формула Гладстона -Дейла
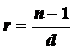 ,
,
где
d - плотность вещества, n - показатель преломления,
r - удельная рефракция. Эта величина представляет собой постоянный коэффициент характерный именно для данного вещества и определяется его молекулярным строением.
Необходимо отметить, что эта величина изменяется для различных веществ в небольших пределах.
Более точной формулой, описывающей связь между плотностью и показателем преломления, считается уравнение Лорентц-Лоренца.
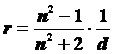
Однако, для растворов в интервале показателей преломления от 1.3 до 1.6, которые соответствуют показателям преломления живой клетки, данное выражение практически не отличается от уравнения Гладстона -Дейла. Позднее было введено понятие молекулярной рефракции
![]() ,
,
Здесь М- молекулярный вес вещества.
Остановимся немного подробнее на тех физических эффектах, которыми обусловлен процесс рефракциии. Под действием электромагнитного поля, которым является свет, происходит смещение электронов в атомах составляющих молекулы вещества. Возникает так называемая поляризуемость молекул. Причем каждое вещество характеризуется своей мерой поляризуемости - a. Каждый поляризованный атом излучает новое поле, которое взаимодействует со старым и изменяет его. Это изменение эквивалентно сдвигу фазы первоначального поля, что приводит к замедлению распространения света в веществе, уменьшение скорости света в среде и есть, по сути, рефракция или преломление. Очевидно, что изменение фазы зависит также от количества молекул на пути следования излучения, т.е. толщины среды и концентрации вещества, в результате на выходе из объекта исследования мы получаем некоторую суммарную задержку фазы.
На основании электромагнитной теории было показано, что R= 2,52×10 -24 ×a , где а - постоянный коэффициент, определяющийся поляризуемостью молекул. Т.е. рефракция зависит от числа атомов или молекул данного вещества и меры их поляризуемости.
Взаимодействие происходит на электронном уровне и поэтому эффект взаимодействия суммируется и это позволяет сделать вывод об аддитивности молекулярной рефракции. Это значит, что если мы рассматриваем смесь двух материалов, то показатель преломления смеси равен не просто сумме показателей. Для его определения необходимо учитывать поляризуемость каждой составляющей и числа молекул данного типа. Например, если рассматриваем два вещества с поляризуемостью a1 и a2, то согласно условию аддитивности
aS×N=a1×N1+ a2×N2,
где
N1, N2 - число молекул каждого вещества.
Однако более удобно воспользоваться уравнением Гладстона-Дейла и записать:
![]()
Здесь
n1, n2, n - показатели преломления каждого вещества и их смеси,
d1, d2 - плотности компонентов,
р - весовые проценты.
Правило аддитивности носит достаточно универсальный характер. Оно очень хорошо выполняется для газов и растворов, содержащих простые молекулы. Для сложных молекул, таких, например, как молекулы белка, справедливость данного правила нуждается в доказательстве, т.к. оно не учитывает изменения химического состояния вещества.
Приведенные выше уравнения носят универсальный характер и применяются практически для всех веществ в любом агрегатном состоянии. Как известно, при применении тех или иных методов исследования в каждой новой области складывается своя система терминов и обозначений. Не составило исключения применение рефрактометрии в цитологии. В рефрактометрическом анализе клеток нашла применение следующая запись формулы Гладстона-Дейла
![]() (7.17)
(7.17)
где
n - показатель преломления раствора
nr - показатель преломления растворителя
С - концентрация растворенного вещества в граммах на 100мл раствора,
a - удельный инкремент (приращение) показателя преломления, т.е. величина прироста показателя преломления при увеличении концентрации раствора на 1%. Эта величина и характеризует поляризуемость растворенных веществ.
Такая запись применяется в рефрактометрии биообъектов в первую очередь потому, что определение удельного инкремента показателя преломления для растворов органических веществ экспериментально определить достаточно просто. Эти измерения проводились, наиболее интенсивно начиная с середины 50-х годов. О них мы расскажем в следующем разделе. Знание инкремента является необходимым, но не достаточным условием для определения плотности и показателя преломления клетки и ее органел, а именно это нам необходимо, чтобы описать процесс распространения оптического излучения в веществе.
Плотность и показатель преломления цитоплазмы, ядра других органел клетки анализировались многими исследователями. При этом различные физические методы измерений позволяют определять, как плотность, так показатель преломления составляющих клетки.
Показатель преломления определяется только оптическими методами, а плотность может быть измерена также при помощи гисторентгенографии. Этот метод основан на измерении поглощения рентгеновского излучения веществом клетки.
Учитывая, что органелы клетки представляют собой сгустки вещества в цитоплазме, перепад или, как говорят, градиент показателя преломления может составлять 0,1-0,01. В таблице 7.1 приведены значения градиентов показателя преломления, рассчитанные по измеренным данным плотности вещества внутри клетки. Знание градиента очень важно для анализа процесса распространения оптического излучения через живую клетку.
В предыдущем разделе мы говорили о плотности и показателе преломления клеточного вещества, не останавливаясь на вопросе из чего собственно состоит живая клетка. Рассмотрим это подробнее.
Живую клетку можно рассматривать как водный солевой раствор, в котором находятся различные органические вещества. Вода составляет около 70% всей массы клетки. По концентрации солей внутриклеточная вода практически совпадает с физиологическим раствором. Показатель преломления ее принимают равным 1,334. Концентрация растворенных в клетке органических веществ составляет 20-30%. Их иногда называют сухой массой клетки. Для таких растворов хорошо применима уравнение Гладстона-Дейла в виде представленном формулой (7.17). Согласно этому уравнению, для того чтобы определить концентрацию органических веществ в клетке, что является нашей основной задачей, необходимо измерить ее показатель преломления и определить инкремент показателя преломления неводных компонент. Как измерять показатель преломления живой клетки мы будем говорить в других разделах, а здесь рассмотрим проблему определения инкремента веществ, составляющих клетку. Согласно определению, эта величина равна приросту показателя преломления при увеличении концентрации вещества на 1%. Очевидно, что измерить ее непосредственно в живой клетке невозможно. Поэтому инкремент различных составляющих живой клетки определяют путем косвенных расчетов и экспериментально на выделенных субстратах.
Сухая масса клетки состоит из органических и минеральных веществ. Большую часть сухой массы составляют макромолекулы-белки, нуклеиновые кислоты и полисахариды. Их молекулярная масса составляет от 10 тыс. до 1 млн. В процессе жизнедеятельности клетки они синтезируются из малых молекул: аминокислот, нуклеотидов и сахаров. Из примерного состава клетки млекопитающего видно , что основную часть сухой массы-65% составляют белки + ДНК и РНК, 7%- полисахариды, 15%- липиды.
Многочисленные исследования показали, что данная величина для различных белков практически одинакова и составляет 0.00185см3/г. Отклонения не превышают 5-6%.
Для углеводов (сахароза, крахмал) удельный инкремент показателя преломления меньше и составляет 0.0014-0.0015 см3/г. Однако, как показали исследования более высокие молекулярные соединения - полисахариды, а также углеводы связанные с белками имеют инкремент близкий к белку- 0.0017-0.00178 см3/г.
Липиды в свободном виде также имеют более низкий инкремент (в среднем 0.014 см3/г). Однако, в комплексных соединениях их инкремент также близок к характеристикам белка.
Удельный инкремент показателя преломления минеральных солей варьируется в широких пределах: хлорид натрия 0.163, хлорид кальция
В результате анализа различных компонент клетки можно было с достаточным основанием принять значение удельного показателя преломления всех неводных компонент клетки равным
С(в граммах на 100 мл)![]()
Данное выражение будет ключевым при дальнейшем анализе и интерпретации измерений проводимых при микроскопии живых клеток.
Прежде чем провести анализ хода оптических лучей в клетке с учетом разработанной нами модели рассмотрим изображения живых неокрашенных клеток, полученных в обычном световом микроскопе.
| а) |
б) |
|
|
|
а – эритроцита
б - эпителиальной ядерной клетки
Рисунок 7.6
В качестве примера на рисунке 7.6 а и б представлены изображения двух различных клеток: эритроцита и эпителиальной ядерной клетки соответственно. Живые клетки находились в физиологическом растворе, показатель преломления которого был равен показателю преломления внутриклеточной воды. На изображении хорошо видна модуляция интенсивности, т.е. возникает впечатление, что клетка поглотила часть проходящего излучения. Однако мы знаем, что длина волны 0.6328 мкм, которая использовалась в микроскопе при получении данных изображений, практически не поглощается живой не окрашенной клеткой. Следовательно, модуляция, которую мы наблюдаем в изображении, вызвана другими причинами. Чтобы ответить на этот вопрос мы должны рассмотреть процесс регистрации света. Существующие в природе позволяют приемники оптического излучения позволяют регистрировать только его интенсивность, которая представляет собой квадрат комплексной амплитуду света. Поэтому такие приемники называются квадратичными. Комплексная амплитуда электромагнитного поля записывается в виде:
E=A×exp(-ij),
где
А - амплитуда,
j - фаза поля.
Интенсивность поля определяется выражением:
I=êE ê2= A×exp(-ij)× A×exp(+ij)=A2.
Таким образом, интенсивность света, которая фиксируется квадратичным регистратором, пропорциональна квадрату амплитуды поля. То есть мы не можем напрямую зарегистрировать изменение фазы поля прошедшего через объект, а в наблюдаемом изображении микрообъекта мы видим модуляцию интенсивности вызванную другими причинами. Постараемся выявить эту причину, анализируя процесс распространения света через вещество клетки с учетом явлений рефракции и дифракции. Рассмотрим в качестве примера модель эритроцита. Он представляет собой безъядерную клетку с постоянным распределением вещества-гемоглобина внутри, показатель преломления которого n1. Пусть эта клетка расположена в среде с показателем преломления n2¹n1. Тогда лучи будут преломляться на границе раздела двух сред, а т.к. поверхность эритроцита имеет форму тора, которая в сечении представляет собой "гантель", то каждая ее половинка будет работать как маленькая линза, т.е. немного фокусировать свет. В результате этого происходит перераспределение энергии за счет рефракции света и данный эффект мы наблюдаем в виде изменения яркости изображения на регистраторе.
Другой пример эпителиальная ядерная клетка. На рисунке 7.6 б мы также видим модуляцию интенсивности, однако, причины ее несколько другие. Часть оптического излучения, также как и в случае с эритроцитом преломляется на плавных неоднородностях сравнительно большого размера внутри ядра и цитоплазмы - точки А и В. Некоторые лучи встречают на своем пути мелкие неоднородности, которые меньше длины волны. К ним относятся мембрана, толщина которой составляет всего около 5 нм, мелкие гранулы и т.п. На этих неоднородностях происходит дифракция света, в результате чего эти включения можно рассматривать, как источник вторичных волн.
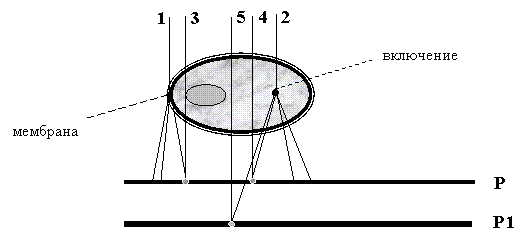 |
Рисунок 7.7.
На рисунке 7.7 схематически представлен процесс дифракции на мембране и мелком включении - лучи 1 и 2.
В некоторых книгах при описании этого процесса используют понятия рассеяния света в среде. Дифрагированное излучение выходит из объекта и на регистраторе в плоскости Р взаимодействует с не рассеянным светом, прошедшим через другие участки клетки - лучи 3 и 4. При этом наложении происходит пространственное перераспределение энергии оптического излучения, которое называется интерференцией света. Необходимо отметить, что данное явление наблюдается только при регистрации интенсивности поля. Возникшая в результате интерференции модуляция изображения не имеет отношения к поглощению света в живой клетке, а определятся наличием маленьких, но достаточно плотных включений. Наблюдаемый на рис. 1.4б ореол вокруг клетки определяется дифракцией на мембране. Нетрудно проверить наши заключения. При расфокусировке, т.е. смещении плоскости регистрации на рис. 1.5 в положение Р1, должно изменяться изображение, т.к. дифрагированный луч интерферирует с другим не отклоненным лучом. На рис.1.6 представлено два изображения той же эпителиальной клетки, но с различными фокусировками микроскопа. Нетрудно заметить различия в изображениях, вызванные эффектом дифракции света на мембране клетки.
Простейшие соображения, которые мы использовали для описания процесса распространения света в неоднородной среде, не позволяют, конечно, получать количественные данные о структуре живой клетки. Для этого необходимо использовать более строгие физические модели, которые позволили бы связать некоторой формулой параметры оптического излучения, прошедшего через объект с его внутренней структурой.
Процесс распространения оптического излучения в неоднородной среде описывается достаточно сложным дифференциальным уравнением - волновым уравнением Гельмгольца. Решением данного уравнения является искомое нами выражение, определяющее связь между параметрами объекта и поля, прошедшего через него. Общих методов решения этого волнового уравнения для произвольного объекта не существует. Поэтому при исследовании трехмерных микрообъектов используются наиболее простые модели среды и процесса распространения, которые и определяют вид решения данного волнового уравнения. Далее мы остановимся подробнее на двух основных методах описания процесса распространения света в неоднородной среде, которые соответствуют двум различным моделям объектов: теория однократного рассеяния и метод геометрической оптики.
Приближение однократного рассеяния впервые применил М. Борн в квантовой механике. Поэтому данное приближение в литературе называется борновским. В оптике задолго до этого Релей применил похожий метод для анализа рассеяния света на прозрачных телах и, поэтому, иногда указанное приближение называют релеевским. Данный метод описания распространения оптического излучения в среде используется для такого вида объектов, которые отвечают следующим условиям:
- флуктуации параметров среды относительно среднего уровня достаточны слабы
- рассеянное поле мало по сравнению с полем первичной волны
При нарушении указанных условий необходимо учитывать двух- , трех- и т.д. кратное рассеяние света. Однако, такая теория очень сложна и практически не применяется. Приведем некоторые уравнения описывающие процесс однократного рассеяния. Пусть оптическое излучение Е0 падает на объект, занимающий объем V(![]() ) , с распределением показателя преломления внутри его n (
) , с распределением показателя преломления внутри его n (![]() ). Согласно первому условию представим распределение показателя преломления внутри объекта:
). Согласно первому условию представим распределение показателя преломления внутри объекта:
![]()
где
![]() - среднее значение,
- среднее значение,
![]() - флуктуация n.
- флуктуация n.
Полагая, согласно второму условию, что рассеянное поле E1<<E0 , можно записать решение уравнения Гельмгольца в виде:
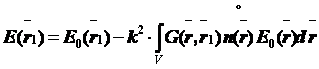 ,
,
где
![]() - волновое число,
- волновое число,
l - длина волны света.
Функция  носит название функции Грина и в нашем случае, как видно из уравнения, представляет собой поле точечного источника. Таким образом, приближение однократного рассеяния представляет объект набором точечных рассеивателей, на которых происходит дифракция падающей волны. В области наблюдения рассеянное поле взаимодействует с падающим излучением и формирует изображение объекта. На нашей модели, представленной на рисунке 7.7 это соответствует, например, лучам 4 и 2. Нетрудно заметить, что в приближении однократного рассеивания нет ограничений на градиент показателя преломления внутри микрообъекта. Оно очень хорошо описывает процессы дифракции на мембранах клетки и клеточных структур и малых органелах, поэтому данная теория применяется для описания процесса формирования изображения в фазовоконтрастной микроскопии.
носит название функции Грина и в нашем случае, как видно из уравнения, представляет собой поле точечного источника. Таким образом, приближение однократного рассеяния представляет объект набором точечных рассеивателей, на которых происходит дифракция падающей волны. В области наблюдения рассеянное поле взаимодействует с падающим излучением и формирует изображение объекта. На нашей модели, представленной на рисунке 7.7 это соответствует, например, лучам 4 и 2. Нетрудно заметить, что в приближении однократного рассеивания нет ограничений на градиент показателя преломления внутри микрообъекта. Оно очень хорошо описывает процессы дифракции на мембранах клетки и клеточных структур и малых органелах, поэтому данная теория применяется для описания процесса формирования изображения в фазовоконтрастной микроскопии.
Теория однократного рассеивания позволяет описывать процесс дифракции на плоских объектах, поэтому она получила очень широкое распространение для описания процесса формирования изображения оптическими системами. Аббе на основании этих уравнений разработал дифракционную теорию формирования изображения в микроскопии, которая лежит в основе современных методов оценки качества оптических систем и изображений ими формируемыми.
В тех случаях, когда неоднородности внутри объекта слабо изменяются в пределах длины волны света, т.е. они являются гладкими, рассеяние на большие углы пренебрежимо мало. Поэтому изменения зондирующего излучения определяются теми неоднородностями, которые лежат на пути волны, т.е. в окрестности луча, соединяющего место входа излучения в объект с точкой выхода. Очевидно, что в данном случае нельзя использовать гипотезу об однократном рассеянии, т.к. свет фактически многократно рассеивается на очень малый угол. Обычно в таком случае правильнее говорить не о дифракции света на пространственных неоднородностях, а о его рефракции. Для описания процесса распространения света в таких объектах применяют метод геометрической оптики. Основными условиями, накладываемыми на характеристики объекта, необходимыми для применимости данного метода являются:
-малое изменение параметров сред в пределах длины волны;
-относительные флуктуации параметров среды достаточно малы.
Решение уравнение Гельмгольца для модели объекта, отвечающей указанным условиям, было предложено Р.Дебаем в1911 г. Согласно приближению геометрической оптики поле E(x,y,z) в каждой точке внутри объекта имеет структуру плоской волны:
![]()
где
А - амплитудa,
j - фаза волны и ее градиент медленно изменяются на расстоянии, сравнимым с длиной волны, по сравнением с самими величинами А и j.
Используя данное представление поля можно получить приближенное уравнение, которое связывает фазу поля прошедшего через объект с распределением показателя преломления внутри его:
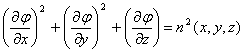 . (7.18)
. (7.18)
Это уравнение получило название уравнение эйконала. Решение данного дифференциального уравнения возможно только в том случае, когда известна траектория лучей, по которым распространяется излучение. В общем случае эта траектория удовлетворяет принципу Ферма. В простейшем случае он гласит: свет всегда распространяется в пространстве между двумя точками по тому пути, вдоль которого время его прохождения наименьшее. В общем случае свет распространяется по некоторой кривой. Если тем или иным способом траектория распространения света s известна, то эйконал j находится по формуле:
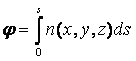 (7.19)
(7.19)
Данное выражение устанавливает связь между фазой прошедшей волны и показателем преломления внутри объекта.
Нетрудно заметить основное различие между выражениями, описывающими связь между распределением показателя преломления внутри объекта и полем на его выходе, в случае однократного рассеяния и метода геометрической оптики. В первом случае интегрирование ведется по всему объекту, а во втором только вдоль одной линии s внутри его.
Напомним, что объекты, которые изменяют фазу зондирующего оптического излучения, называют фазовыми. Измерение фазы прошедшего излучения позволяет получить информацию, по которой можно судить о распределении вещества внутри клетки. Однако, это возможно только в том случае, когда уравнение, описывающее зависимость между показателем преломления и фазой света известно, т.е. известна траектория распространения света внутри объекта. В общем случае определить отклонение траектории от прямолинейной не представляется возможным. В микроскопии живых клеток используются такие условия, когда можно пренебречь рефракцией и дифракцией зондирующего излучения. Предполагается, что свет распространяется прямолинейно через клетку, распределение показателя преломления внутри которой n(x,y,z). В этом случае поле, прошедшее через объект, для падающей на него плоской монохроматической волны может быть представлено в виде:
![]()
где
A0 - амплитуда падающей волны,
j0 - начальная фаза.
Величина

представляет собой интеграл от переменного внутри клетки показателя преломления вдоль невозмущенного луча. Для фазовых объектов эта величина определяет эйконал или оптическую длину пути света. Понятие оптической длины пути очень важное и понадобится нам в дальнейшем. Поэтому поясним его на простом примере. Пусть у нас есть объект в виде пластины равной толщины с постоянным показателем преломления внутри n2, которая находится в среде с постоянным показателем преломления n1.
Монохроматическое оптическое излучение прошедшее через данный объект по нормали к поверхности изменит свою фазу относительно луча, проходящего вне его, на величину j =(n1-n2)×L, т.е. изменение фазы или оптическая длина пути всегда определяется произведением показателя преломления на размера объекта. Таким образом, не зная размер клетки нельзя по фазе определить ее показатель преломления и наоборот. Распределение фазы поля на выходе из фазового объекта измерить невозможно без использования специальной техники. Эта задача решается при помощи специализированных приставок к микроскопам, которые обеспечивают перенос фазового распределения из плоскости В в плоскость приемника излучения без искажений с требуемым увеличением и специальную интерференционную регистрацию. Заметим, что формирование фазового изображения имеет свои особенности, которые мы рассмотрим позднее. Анализ распределения плотности внутри клетки по фазовым измерениям лег в основу такого метода количественной цитохимии, как микроинтерферометрия.
Метод геометрической оптики применяется в основном для анализа фазовых объектов, когда поглощением света в объекте можно пренебречь. Однако, при исследовании окрашенным препаратов, а также при наличии в микрообъекте пигментов поглощение света может быть существенным. Распространение оптического излучения в поглощающем объекте, в случае отсутствия рассеяния света, определяется уравнением Бугера-Бера. Данный закон основан на уравнении переноса излучения и описывает распространение интенсивности света в среде без учета волновых эффектов. Запишем этот закон для произвольного распределения концентрации поглощающего вещества внутри клетки с(x,y,z). В этом случае математическая запись его имеет вид:
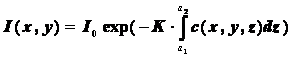 ,
,
где
K - удельный показатель поглощения, определяемый свойствами вещества,
Io- интенсивность освещающего пучка, I - интенсивность прошедшего излучения.
В такой записи данное уравнение можно интерпретировать следующим образом. На точку а1 на поверхности клетки (рисунок 7.8) падает луч интенсивности I0, который распространяется вдоль линии L, и выходит в точке а2. В каждой точке внутри клетки поглощение пропорционально концентрации поглощающего вещества с(x,y,z), но в процессе распространения оно накапливается, т.е. интегрируется. При этом очевидно, что концентрация поглощающего вещества усредняется вдоль траектории распространения излучения. Таким образом измерение интенсивности прошедшего через клетку излучения на выходе из нее в плоскости XY (рисунок 7.8) позволяет определять среднюю концентрацию поглощающего вещества. Задача микроскопа в данном случае сводится к переносу распределения интенсивности из плоскости XY в плоскость регистратора без искажений, но с требуемым увеличением.

Рисунок 7.8
Закон Бугера-Бера лег в основу метода цитоспектрометрии, который является одним из важных методов количественной цитохимии.
Подчеркнем , что для его применения необходимо выполнение двух условий. Во-первых, наличие поглощающего оптическое излучение вещества внутри клетки, и, во-вторых, выполнение для него закона Бугера-Бера.
Если сравнить эйкональное уравнение с законом Бугера-Бера, то не трудно заметить, что в них много общего. Необходимо только всегда помнить, что в первом случае измеряется интенсивность прошедшего поля, а, во втором, - фаза. Главное, что общего в обоих уравнениях - условие прямолинейности распространения излучения в среде. Данное условие общепринято сейчас для микроскопии живых клеток. Это позволяет проводить количественную обработку результатов измерений интенсивности и фазы прошедшего излучения и судить по ним о внутренней структуре клетки.
Флуоресцентное излучение возникает внутри исследуемого объекта и носит эмиссионный характер. Каждый источник такого излучения можно рассматривать как точечный, т.е. излучающий равномерно во все стороны. При этом он может быть расположен в любой точке внутри объема живой клетки. Флуоресцентное излучение является монохроматическим, но полностью некогерентным, поэтому можно измерять только его интенсивность. При описании процесса распространения флуоресцентного излучения среде не учитывают его поглощения и преломления. Это оправдано, т.к. поглощение в живой клетке практически отсутствует, а преломление не сказывается на изменении интенсивности излучения. При наблюдении мы регистрируем все излучение, вышедшее из клетки. На рисунке 7.9 схематически представлен ход лучей в эмиссионном объекте.
B
![]()

Рисунок 7.9.
Из рисунка видна, что в каждую точку плоскости В на выходе объекта приходят лучи из различных излучающих точек расположенных внутри трехмерного объекта. Очевидно, что в плоскости В получается сильно размытое изображение. Но это характерно только для объемных микрообъектов. В тех случаях, когда мы исследуем плоские препараты, плоскость B совмещена с объектом, и мы наблюдаем во флуоресцентном микроскопе резкое изображение. Для исследования живых клеток, которые являются трехмерными объектами, при измерении концентрации флюоресцирующего вещества в различных точках внутри клетки приходится применять, в качестве приставки к микроскопу, специальную сканирующую технику. Это легло в основу такого метода количественной цитохимии, как микроспектроскопия.
В объектах, обладающих указанным свойством, для их исследования измеряется разность фаз между обыкновенным и необыкновенным лучами. Каждый из них распространяется в среде независимо. Поэтому двулучепреломляющий объект можно рассматривать, как два фазовых объекта с различными распределениями показателя преломления no и ne. Для описания процесса распространения света в них используются такие же законы распространения, как и в фазовых объектах, т.е. предполагается прямолинейное распространение излучения и используется эйкональное уравнение (7.18 ). В этом случае разность в значениях фаз для обыкновенного и необыкновенного лучей на выходе из объекта будет описываться выражением:
j=(n0-ne)×l,
где
l- размер объекта вдоль луча.
Необходимо только учитывать, что мы должны регистрировать разность фаз между лучами, поляризованными в двух взаимно перпендикулярных направлениях. Для этого в микроскопии используются специальные приспособления, которые обеспечивают измерение указанной величины.
Методы исследования биологических объектов при помощи микроскопов имеют очень давнюю историю и позволили за это время получить ряд фундаментальных важнейших результатов. Несмотря на то, что оптическая микроскопия насчитывает более 300 лет она не утратила свои позиции, а введение новых методов и техники исследований (флуоресцентная микроскопия, конфокальная микроскопия, микроскопия ближнего поля) определяет ее приоритетное значение в настоящее время.
Микроскоп вошел в практику научных исследований с того момента, как были подмечены увеличительные свойства воды. И хотя увеличительные стекла и другие виды простейших микроскопов все еще применяются в настоящее время, область микроскопии столь велика, что вряд ли первые исследователи могли себе такое представить. Первые наблюдения микроорганизмов были сделаны А.Левенгуком еще в 1673 году. За три столетия микроскоп, конечно существенно преобразился, но его суть, как прибора для получения увеличенных изображений объектов невидимых невооруженным глазом осталась неизменной. Микроскоп и сейчас является главным инструментом исследователя морфолога и врача-лаборанта. Несмотря на значительные успехи полученные другими методами исследования клеток, для анализа живых одиночных клеток наиболее перспективна оптическая микроскопия. С этим связан буквально бум, который происходит в последние годы, в появлении принципиально-новых схем и методов оптической микроскопии. Можно сказать, что развитие биологических наук в некоторой степени зависит от создания нового класса микроскопов и техники, однако наиболее популярным на сегодняшний день является микроскоп, имеющий такую же оптическую конструкцию, как и те микроскопы, которые создавались в первой половине 20-го столетия. Эти микроскопы все еще широко применяются, так как они сравнительно не дороги, просты в использовании и надежны для повседневных, рутинных исследований, составляющих основу любой научной работы. В настоящем разделе мы, наряду с изложением традиционных вопросов микроскопии, постарались осветить современные разработки в данной области, которые уже нашли применение прижизненной цитологии клетки. Сделана также попытка с одной стороны, указать на те перспективные направления в микроскопии, которые представляют наибольший интерес для медицины и, с другой стороны, на возможность удовлетворения этого интереса современными методами оптоэлектроники и компьютерного анализа оптической информации.
Методы исследования биологических объектов при помощи микроскопов имеют очень давнюю историю и позволили за это время получить ряд фундаментальных важнейших результатов. Первые наблюдения микроорганизмов были сделаны А.Левенгуком еще в 1673 году. За три столетия микроскоп, конечно существенно преобразился, но его суть, как прибора для получения увеличенных изображений объектов невидимых невооруженным глазом осталась неизменной. Микроскоп вошел в практику научных исследований с того момента, как были подмечены увеличительные свойства воды. И хотя увеличительные стекла и другие виды простейших микроскопов все еще применяются в настоящее время, область микроскопии столь велика, что вряд ли первые исследователи могли себе такое представить.
Можно сказать, что развитие биологических наук в некоторой степени зависит от создания нового класса микроскопов и техники, однако наиболее популярным на сегодняшний день является микроскоп, имеющий такую же оптическую конструкцию, как и те микроскопы, которые создавались в первой половине 20-го столетия. Микроскоп и сейчас является главным инструментом исследователя морфолога и врача-лаборанта. Несмотря на значительные успехи полученные другими методами исследования клеток, для анализа живых одиночных клеток наиболее перспективна оптическая микроскопия. С этим связан буквально бум, который происходит в последние годы, в появлении принципиально-новых схем и методов оптической микроскопии. В настоящем разделе мы, наряду с изложением традиционных вопросов микроскопии, постарались осветить современные разработки в данной области, которые уже нашли применение в прижизненной цитологии клетки. Сделана также попытка с одной стороны указать на те перспективные направления в микроскопии, которые представляют наибольший интерес для медицины и, с другой стороны, на возможность удовлетворения этого интереса современными методами оптоэлектроники и компьютерного анализа оптической информации.
Современные микроскопы выглядят достаточно сложными, автоматизированными и многофункциональными системами. Однако, знание основных узлов микроскопа и понимание принципов их действия необходимы для освоения этих сложных приборов. Поэтому рассмотрим оптическую схему наиболее типичного микроскопа, представленную на рисунке
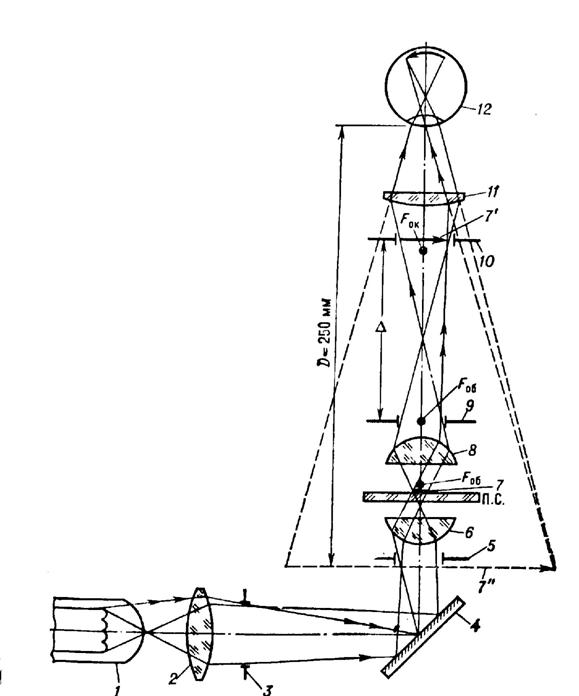
Рисунок 7.10 – Принципиальная оптическая схема микроскопа
Условно микроскоп можно разбить на четыре узла: осветительная система позиции 1-6 рисунка, препарат 7, с плоскостью препарата сопряжена полевая диафрагма окуляра 10 и полевая осветительная диафрагма 3, апертурная диафрагма 9,с корой сопряжена ирисовая диафрагма 5, окуляр 12. Рассмотрим ход лучей в микроскопе. Объект 7, обозначенный стрелочкой, расположен на предметном столике 7 перед микробъективом 8, на расстоянии несколько большем его фокусного расстояния Fоб. Он строит действительное, увеличенное и перевернутое изображение 7' в плоскости диафрагмы 10. Данное промежуточное изображение расположено за передним фокусом окуляра 12. Поэтому окуляр строит мнимое увеличенное изображение 7'' на расстоянии D= 250 мм от глаза наблюдателя. Такое расстояние считается наилучшим с точки зрения физиологических свойств глаза. Если мы хотим получить действительное изображение объекта на телевизионном приемнике или фотопленке, то достаточно окуляр сдвинуть так, чтобы изображение 7' оказалось перед фокусом окуляра. Основные характеристики микроскопа: видимое увеличение Г, линейное поле зрения 2y, числовая апертура NА.
Видимое увеличение микроскопа равно произведению увеличения микрообъектива Гоб и окуляра Гок. Увеличение объектива определяют выражением
Гоб=![]() ,
,
а увеличение окуляра
Гок=![]() ,
,
где
fоб, fок - их фокусные расстояния,
D - расстояние между задним фокусом микрообъектива и передним фокусом окуляра.
Линейное поле зрения микроскопа 2y зависит от углового поля окуляра 2w': y'=fок× tgw', а также увеличения микроскопа Г.
2y=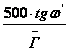
Из формулы видно, что при больших увеличениях микроскопа линейное поле зрения мало.
Числовая апертура микроскопа определяет его основные характеристики: светосилу и разрешающую способность. Числовой апертурой называют произведение показателя преломления среды, в которой находится объект, на синус апертурного угла:
NА=n×sinq.
где q- угол между оптической осью и крайним лучом, попадающим в объектив из фокуса микрообъектива.
Основными узлами микроскопа являются осветительная система, микрообъектив, предметный столик и окуляр.
Осветительная система микроскопа состоит из источника оптического излучения и оптической системы, обеспечивающей равномерное освещение объекта. Сложности возникающие при создании осветительных систем вызваны тем, что в микроскопах, особенно с большим увеличением, необходимо применять яркие источники света. Тело накала таких источников, например нить лампы, имеет неравномерную яркость поэтому оно проецируется оптической системой, которая называется конденсором, не точно в плоскость предмета, а ближе или дальше. При таком освещении образуется много рассеянного света, который ухудшает условия наблюдения. Другой проблемой является то, что числовая апертура конденсора должна быть больше или равна числовой апертуры объектива. В противном случае снижается разрешающая способность микроскопа. Решение этих задач привело к созданию различных типов осветительных систем микроскопа. Наибольшее распространение получила схема освещения по Келлеру, которая представлена на рисунке 7.10 позициями 1-6. Она применяется во всех отечественных микроскопах. Не вдаваясь в подробности принципа ее работы можно сказать, что данная схема освещения позволяет получить равномерное освещение поля микроскопа от источника с неравномерной яркостью светящего тела без ухудшения качества изображения. В современных микроскопах, например, конфокальных, а также при использовании лазерных источников излучения применяются другие схемы освещения.
Микробъектив является важнейшей частью микроскопа, определяющей качество изображения и светосилу. Он представляет собой многолинзовую систему, в которой исправлены аберрации искажающие изображение. В зависимости от вида исправленных аберраций объективы делят на следующие основные виды: ахроматы, апохроматы, планахроматы, планапохроматы. Основными характеристиками объектива микроскопа являются увеличение и числовая апертура. Последняя определяет разрешающую способность микроскопа - чем больше числовая апертура, тем лучше разрешающая способность. В зависимости от увеличения и числовой апертуры объективы микроскопов можно разбить на три группы, представленные в таблице 7.2
Таблица 7.2
| малых увеличений и апертур |
Г£10х |
NA£0.2 |
| средних увеличений и апертур |
Г£40х |
NA£0.65 |
| больших увеличений и апертур |
Г>40х |
NA>0.65 |
Числовая апертура объектива зависит от показателя преломления среды, в которой находится препарат. Поэтому для увеличения NА используют иммерсию: воду или масло, показатель преломления которых больше единицы. Микрообъективы, которые могут работать в таких условиях, называют иммерсионными. Современные микрообъективы имеют увеличение до 100х и числовую апертуру до 1.6.
Окуляр представляет собой более простую оптическую систему, чем объектив. Его роль в формировании изображения микрообъекта гораздо менее важная и поэтому требования к нему более низкие. Основной характеристикой окуляра является увеличение, которое изменяется в зависимости от типа от 4х до 15-ти крат.
Предметный столик и другие юстировочные узлы микроскопа составляют основу его механической части. Предметный столик должен решать две задачи: во-первых, обеспечивать крепление препарата и легкий доступ к нему наблюдателя, во-вторых, точное перемещение препарата по двум координатам. В современных микроскопах требуемая точность перемещения составляет от одного до нескольких микрон, а величена перемещения 2-3 сантиметра. В настоящее время применяется автоматическое перемещение кареток столика по двум координатам, управляемое от ЭВМ. Другим важным механическим узлом микроскопа является устройство, обеспечивающее его фокусировку. Как правило, фокусировка микроскопа производится передвижением тубусодержателя, в котором крепится объектив и окуляр, с помощью грубого и микротрендного механизмов. При помощи них тубус, как единое целое, приближается или удаляется от объекта до тех пор пока оператор не принимает решение о наилучшей фокусировке на препарат.
Понятие качество изображения применительно к микроскопии определяет способность его оптической системы создавать геометрически подобные предмету изображения, в которых отдельные детали и контраст воспроизведены с достаточной точностью. Качество изображений, формируемых микроскопом, в идеальном случае определяется законами дифракционной оптики, однако, в действительности оно зависит от таких особенностей прибора, как остаточные аберрации микрообъектива, освещенность и контраст предметов, наличие дефектов в оптическом стекле, ошибки изготовления и сборки, а также особенности приемника.
В микроскопии общепринято использовать для оценки качество изображения понятие разрешающей способности. Различают два вида разрешения: латеральное (поперечное) и аксиальное (продольное)- вдоль оптической оси. Остановимся подробнее на этих понятиях. При формировании изображения любой оптической системой в том числе и микроскопом каждая бесконечно малая светящаяся точка в объекте преобразуется в эллипсоид, вытянутый вдоль оптической оси. В сечении перпендикулярном оптической оси, изображение точки представляет собой яркое пятно, которое получило название диск Эри, с концентрическими темными и светлыми кольцами постепенно убывающими по яркости в изображении. Процесс формирования данного пятна и колец его окружающих хорошо описывается законами дифракционной оптики. В диске Эри сосредоточено 84% всей энергии и его размер определяется выражением:
![]()
где
NA- числовая апертура микрообъектива,
l- длина волны света.
Предел разрешения микроскопа определяется при сближении двух светящихся точек до такого расстояния, когда в пространстве изображений падение освещенности между ними становится незаметным для глаза и визуально две точки сливаются в одну. Для количественного определения этого предела используется критерий Рэлея. Согласно критерию Релея изображения двух близких самосветящихся (некогерентных) точек можно еще считать раздельными, если центр дифракционного пятна, соответствующего одной точке, совпадает с первым дифракционным минимумом для второй точки.
В этом случае поперечная разрешающая способность объектива равна:
![]() (7.19)
(7.19)
Расчеты показывают, что при таком расстоянии между точками в промежутке между ними освещенность составляет 80% от освещенности в максимуме. Известно, что человеческий глаз способен различать контраст в освещенности 4%. Этому соответствует расстояние между точками ![]() , т.е. разрешающая способность лучшая, чем по критерию Рэлея. Из формулы видно, что определяющую роль в разрешающей способности играет числовая апертура объектива. Для ее повышения в микроскопии используют иммерсионную жидкость с показателем преломления n>1, которой заполняют пространство между микрообъективом и препаратом. Это позволяет довести числовую апертуру до значения 1.4, в то время как "сухие" объективы имеют NA~0.95. Нетрудно рассчитать, что разрешающая способность в видимой области может достигать 0.2 мкм.
, т.е. разрешающая способность лучшая, чем по критерию Рэлея. Из формулы видно, что определяющую роль в разрешающей способности играет числовая апертура объектива. Для ее повышения в микроскопии используют иммерсионную жидкость с показателем преломления n>1, которой заполняют пространство между микрообъективом и препаратом. Это позволяет довести числовую апертуру до значения 1.4, в то время как "сухие" объективы имеют NA~0.95. Нетрудно рассчитать, что разрешающая способность в видимой области может достигать 0.2 мкм.
Однако, все это справедливо только для абсолютного контраста, когда мы рассматриваем две яркие точки на темном поле. Для полутонового объекта оценка качества изображения по разрешающей способности не отражает всей картины и необходимо использовать более сложные и не столь наглядные характеристики оптических систем. В качестве такой характеристики наиболее часто используют оптическую передаточную функцию (ОПФ) или, как ее еще называют, частотно-контрастную характеристику (ЧКХ). Рассмотрим это понятие подробнее.

Вверху – распределение освещенности в плоскости изображения ;
0,1 – дифракционные максимумы;
a,b – апертурная диафрагма
Рисунок .7.11 –Схема образования изображения несамосветящегося объекта по Аббе.
Пусть объект (рисунок.7.11 ), который мы рассматриваем в микроскоп, представляет собой решетку с абсолютным контрастом и синусоидальным пропусканием амплитуды поля, т.е. описывается выражением
![]()
где
d1 -период решетки,
К=1-коэффициент контраста.
На него перпендикулярно плоскости, к которой он расположен, падает плоская волна света (центральное освещение по Келлеру) с амплитудой А0. На решетке происходит дифракция света при этом свет "расщепляется" на три составляющие, которые получили название нулевого(0), плюс первого (+1) и минус первого (-1) порядков дифракции. Нулевой порядок распространяется без отклонений, а (+1) и (-1) порядки распространяются под углами +sinq1=l /d1 и -sinq1=l/d1 к оптической оси. Угол дифракции зависит от периода решетки и длины волны света.
Из рисунка 7.11 видно, дифрагированное излучение не попадает целиком в объектив, если период решетки достаточно большой. Это приводит к тому, что контраст изображения решетки будет меньше, чем исходный, т.е. К<1. Если мы построим зависимость контраста от пространственной частоты решетки w=1/d, то получим функцию представленную на рис.2.4. Данная функция получила название ОПФ или ЧКХ и она позволяет полностью определять качество изображения, формируемого любой оптической системой. Нетрудно заметить, что для некоторой частоты решетки wкр=1/dкр дифракционные порядки пойдут под таким большим углом к оптической оси, что не попадут в объектив микроскопа с числовой апертурой NA. Тогда контраст в изображении решетки будет равен нулю и она не будет разрешаться данным прибором. Нетрудно заметить, что dкр =l/sinqкр с точностью до константы совпадает с разрешающей способностью микроскопа, а sinqкр равняется числовой апертуре его объектива. Фактически wкр. определяет разрешающую способность микроскопа. Согласно теории рядов Фурье каждый объект может быть представлен в виде суммы синусоидальных решеток различной частоты и контраста. Таким образом ОПФ определяет искажение каждой частоты составляющей объект и всего объекта в целом при формировании изображения оптической системой микроскопа. В оптике принято считать, что ОПФ наиболее полно определяет качество изображения и позволяет судить о том, какие детали изображения искажаются в большей степени. Как правило, ОПФ определяют экспериментально для каждого конкретного прибора, что позволяет учитывать аберрации, недостатки сборки и стекла и т.д. Вид ОПФ может существенно изменяться от прибора к прибору, при этом wкр и разрешающая способность остаются неизменными при неизменной числовой апертуре объектива. Поэтому микроскопы различных фирм с одинаковой разрешающей способностью строят различные по качеству изображения. Тем ни менее в повседневной практике использование ОПФ не очень удобно и применяется понятие разрешающей способности.
Исследования в области радиофизических и оптических измерений показали, что при достаточно точной регистрации рэлеевский предел может быть существенно превзойдён. Было доказано, что разрешающая способность микроскопа определяется не аппаратными свойствами самого прибора, т.е. его ОПФ, а точностью измерения выходного сигнала. Следовательно, при высокоточных измерениях изображения принципиально возможно достижение сверхразрешения в оптической микроскопии.
Восстановление изображения со сверхвысоким разрешением представляет собой двухэтапный процесс. На первом этапе осуществляется регистрация изображения с максимально высокой точностью. На втором этапе на ЭВМ решается обратная задача редукции к идеальному прибору, которая сводится к компенсации ОПФ. Такая реконструкция изображений осуществляется при знании передаточной функции с использованием специальных алгоритмов. Теоретические оценки и экспериментальные исследования данного метода показали возможность получения разрешающей способности в оптическом микроскопе » 0.1 – 0.01 мкм. Фактически появляется возможность изучения микрообъектов с детализацией аналогичной электронной микроскопии на базе оптического микроскопа.
Однако, получение сверхразрешения выдвигает высокие требования к прибору: во-первых, необходима высокая точность регистрации изображений в микроскопе, и, во-вторых, полная автоматизация процесса измерения.
Продольное разрешение микроскопа в литературе иногда называют глубиной резкого изображения. Оно характеризует возможные пределы перемещения плоского объекта без заметного ухудшения резкости изображения. Определить продольное разрешение можно по аналогии с поперечным - по размеру диска Эри вдоль оптической оси. Дифракционная теория формирования изображения дает следующую величину:
![]()
Из данного выражения видно, что разрешающая способность по глубине обратно пропорциональна квадрату числовой апертуры микрообъектива. Поэтому для микрообъективов с большой числовой апертурой глубина резкости составляет величину порядка длины волны, что требует очень точной фокусировки при анализе изображений. Нетрудно заметить, что определить аксиальную разрешающую способность по аналогии с критерием Релея невозможно, т.к. при наблюдении двух светящихся объектов, расположенных вдоль оптической оси, они будут затенять друг друга, и различить их практически нельзя.
Приведенные выражения для разрешающей способности были получены для плоских объектов согласно дифракционной теории формирования изображения. Их использование для оценки качества изображений трехмерных объектов, каковыми являются живые клетки, требует большой осторожности. В частности, для исследования фазовых объектов, ход лучей в которых описывается эйкональным уравнением, необходимо применять другие оценки.
Принципиальная оптическая схема микроскопа, рассмотренная нами в предыдущем разделе, позволяет реализовать целый ряд методов наблюдения микрообъектов. Выбор того или иного метода обусловлен в первую очередь теми задачами, которые ставит перед собой наблюдатель, а также классом исследуемых объектов. Мы в настоящем разделе остановимся в основном на тех методах, которые нашли наибольшее применение в микроскопии биологических объектов.
Данный метод в проходящем через объект свете наиболее распространен. Ему соответствует схема микроскопа на рисунке 7.10. Его используют для исследования поглощающих объектов. Модуляция амплитуды зондирующего оптического излучения происходит в результате поглощения и рассеяния света на различных неоднородностях внутри объекта. В тех местах, где поглощение отсутствует, свет проходит без изменения и образует в плоскости изображения светлый фон, а поглощающие участки выглядят темными. Контраст в изображении тем лучше, чем больше поглощение. Мы уже указывали, что живые микрообъекты практически прозрачны, и для их исследования методом светлого поля необходимо использовать предварительное окрашивание специальными красителями.
При исследовании сильнорассеивающих микрообъектов малого размера, например, бактерий используется метод темного поля. В данном методе используется специальная схема освещения объекта, которая представлена на рисунке 7.12.

1 – конденсор; 2- препарат; 3- объектив
Рисунок 7.12 – Метод темного поля в проходящем свете
Из рисунка видно, что объект освещается наклонным пучком, а в микрообъектив 3 попадает только излучение, рассеянное микрообъектом 2. Свет, прошедший через те части препарата, где отсутствуют рассеивающие центры, не попадает в микрообъектив и не участвует в построении изображения. Поэтому на этих участках изображение выглядит темным, а рассеивающие объекты светлыми. Конечно, по изображению нельзя определить прозрачны частицы или нет, больший или меньший их показатель преломления по сравнению с окружающей средой.
Метод ультрамикроскопии основан на том же принципе освещения. Только направление освещающего излучения выбирается перпендикулярно направлению наблюдения. Данный метод при использовании ярких источников света позволяет наблюдать микрообъекты, размер которых составляет 0.002 мкм. При этом, конечно, мы не получаем сверхразрешение. Определить размер и форму объекта невозможно, т.к. изображение частицы имеет вид дифракционного пятна.
Как уже отмечалось в предыдущем разделе, живая клетка изменяет только фазу зондирующего оптического излучения. Поэтому для ее исследования были разработаны специальные методы микроскопии- фазовый и интерференционный контраст. Остановимся на первом из них. Метод фазового контраста был предложен Ф.Цернике в 1934 году, который развил теорию метода и применил его на практике. Суть его нетрудно понять, если вспомнить процесс распространения оптического излучения в веществе. При наличии неоднородности в исследуемом объекте в результате дифракции часть света отклоняется от своего прямолинейного распространения. Таким образом, излучение, прошедшее через клетку можно условно разбить на две составляющие: дифракционную и прямолинейную или нулевую. При регистрации изображения происходит интерференция этих двух составляющих поля. В обычном микроскопе эта интерференция практически не заметна. Цернике показал, что, если изменить фазу нулевой составляющей на l/4, то в результате интерференции возникнет довольно контрастная модуляция интенсивности в плоскости изображения. При этом значение интенсивности в каждой точке изображения будет в некотором приближении пропорционально искомому изменению значения фазы поля соответствующей областью объекта. Цернике предложил также простую оптическую схему, реализующую указанное преобразование оптического излучения. На рисунке 7.13 изображена принципиальная схема микроскопа, позволяющего наблюдать фазово-контрастные изображения.

1 – апертурная диафрагма; 2 –конденсор; 3- препарат; 4 – объектив; 5 – фазовая пластинка; 6 - изображение
Рисунок 7.13 –Метод фазового контраста в проходящем свете
Было разработано множество модификаций и усовершенствований данного метода.
Перечислим основные из них.
Темный (негативный) фазовый контраст. В данном случае фазовая пластина совпадает с изображением кольцевой диафрагмы конденсора. При этом части объекта, показатель преломления которых выше показателя преломления среды, выглядят светлее фона.
Светлый (позитивный) фазовый контраст. При этой схеме фазовый слой, осуществляющий сдвиг фазы части поля, покрывает ту часть объектива, которая не совпадает с изображением диафрагмы. Тогда те части объекта, которые плотнее выглядят темнее окружающего фона.
Амплитудный фазовый контраст. Для повышения чувствительности и увеличения контрастности изображения применяют частично поглощающее покрытие в области изображения кольцевой диафрагмы конденсора. Это приводит к ослаблению прямого излучения, что при водит к усилению влияния дифрагированного света и, как следствие, повышению контраста фазового изображения.
Аноптральный контраст. Данная разновидность амплитудного фазового контраста предполагает наличие сильного поглощения в области фазового кольца до 90-98% прямого излучения. Эта модификация метода дает особенно хорошие результаты при анализе бактерий, размер которых составляет несколько микрон.
Многочисленные последующие исследования позволили детально оценить все возможности данного метода. Отметим некоторые особенности изображений, получаемых в фазово-контрастной микроскопии, которые возникают в результате отличий реальных оптических систем от теории построения фазовых изображений.
1. Края объектов окружены ореолом, который выглядит ярким в позитивном фазовом контрасте и темным в негативном.
2. Наиболее ярко выделяются те части изображения живой клетки, где есть значительные изменения показателя преломления внутри ее: мелкие включения, границы клетки и ее органел. Указанное обстоятельство позволяет достаточно просто проводить определение морфометрических характеристик живых клеток по фозовоконтрастным изображениям. Те области объекта, в которых присутствует малое изменение плотности практически не визуализируются, и выглядят однородным фоном на изображении
3. Анализ условий формирования фазово-контрастных изображений показал, что оно позволяет определять только качественную картину распределения фазы поля. Количественное определение фазы в каждой точке поля прошедшего через объект практически невозможно. Это связанно с тем, что распределение интенсивности в фазово-контрастном изображении прозрачного объекта не находится в простой функциональной связи с распределением фазы поля, прошедшего через объект. Указанное обстоятельство не позволило использовать данный метод в аналитический цитохимии.
Тем ни менее простая конструкция микроскопов, реализующих метод фазового контраста сделала их незаменимым инструментом для наблюдения живых микрообъектов.
Интерференционная микроскопия является в настоящее время основным методом измерения плотности вещества внутри живой клетки. Он основан на измерении распределения фазы поля прошедшего через микрообъект. Как следует из названия метода определение фазы основано на эффекте интерференции света. Однако в отличии от фазового контраста, в котором оба итерферирующих пучка света проходят через объект, в интерференционном контрасте каждый пучок формируется отдельным оптическим каналом.
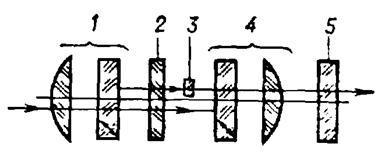
1 –конденсор; 2 – среда в которой находится объект 3, 4 – объектив; 5 -
Рисунок 7.14 Метод интерференционного контраста
На рисунке 7.14 схематически показан принцип действия любого интерференционного прибора в том числе и микроскопа.
Оптическое излучение Е, вышедшее из конденсора, делится в точке 1 на два световых потока
![]()
![]()
где
А1 и А2 - амплитуда поля,
к=2p /l- волновое число.
Распределение фазы в каждом из них одинаково и, как правило, равно константе, т.е. j1(x,y)=j2(x,y)=const. Разделение света производится специальным элементом интерферометра. Один поток проходит через объект с некоторым распределением показателя преломления и он называется - сигнальным, а другой через среду с постоянным показателем преломления и называется - опорным.. Затем оба потока объединяются в точке 2 и направляются по одному пути на регистратор. Очевидно, что все эти преобразования света осуществляются оптическими элементами, вид которых определяет особенности и назначения интерферометра. На них мы остановимся при анализе схем конкретных приборов. Таким образом на регистратор попадает два поля Е'1 и E'2 :
![]()
![]()
где
![]() ,
,
![]() .
.
Переменное распределение фазы во втором потоке и несет информацию о показателе преломления внутри объекта. Эту величину мы и должны измерить для того, чтобы исследовать структуру объекта. Мы уже отмечали, что наблюдение интерференции возможно только при наличии регистрации. В различных приборах используются разные типы регистраторов. Наиболее простой из них- глаза наблюдателя. В современных приборах используется видеокамера. Рассмотрим процесс регистрации подробнее.
Пусть ![]() интенсивность света, которая регистрируется приемником. Представим ее в виде
интенсивность света, которая регистрируется приемником. Представим ее в виде
![]()
![]()
![]() (7.20)
(7.20)
Из формул (7.20) видно, что получение интерферограммы возможно только при наличии двух и более пучков света. Поэтому в интерферометре необходимо разделение исходного излучения и сведение пучков на регистраторе. Из последнего выражения следует, что определение неизвестной фазы ![]() есть задача определения аргумента
есть задача определения аргумента ![]() . Однозначное его восстановление возможно только при известном j1. Различают два типа интерференционных приборов, в зависимости от вида задания фазы опорного потока
. Однозначное его восстановление возможно только при известном j1. Различают два типа интерференционных приборов, в зависимости от вида задания фазы опорного потока ![]() .
.
1. ![]() = const. В этом случае в интерферометре формируются полосы равной толщины и, говорят, что он настроен на "нулевую" полосу. Интерференционная картина описывается следующим выражением:
= const. В этом случае в интерферометре формируются полосы равной толщины и, говорят, что он настроен на "нулевую" полосу. Интерференционная картина описывается следующим выражением:
![]()
2. ![]() . В этом случае опорный пучок направляется под углом a на регистратор и в интерферометре формируются полосы равного наклона. Интерференционная картина описывается следующим выражением:
. В этом случае опорный пучок направляется под углом a на регистратор и в интерферометре формируются полосы равного наклона. Интерференционная картина описывается следующим выражением:
![]()
Наличие данного члена в уравнение приводит к возникновению полос с постоянным периодом на интерферограмме. а наличие переменной фазы приводит к искривлению этих полос. На рисунке 7.15 представлено изображение интерферограммы эритроцита при настройке интерферометра на полосы равного наклона.

Рисунок 7.15
Применение того или иного метода формирования интерферограмм обусловлено в первую очередь методом расшифровки интерферограмм. Под расшифровкой в данном случае понимается восстановление распределения фазы поля сигнального пучка из интерференционной картины. Из уравнения интерферограммы видно, что фазу можно измерять либо в долях длины волны l, либо в угловых градусах. Для измерения разности или сдвига фазы в отдельных точках изображения микрообъекта используют различные приставки к микроскопам, которые называют компенсаторами, например, компенсатор Сенармона. Суть их работы заключается в визуальном сравнении яркости изображения, в измеряемой точке, при двух различных положениях компенсатора. Подробнее с его работой можно познакомиться в паспорте конкретного прибора. Такого рода приставки позволяют проводить измерения сдвига фазы с точностью l/100-l/300. К сожалению, указанные приспособления не позволяют автоматизировать процесс восстановления распределения фазы всего волнового фронта. Отметим еще одну особенность формирования интерференционной картины. Четкие контрастные полосы можно получить только при когерентном излучении. Таким свойством, как мы уже говорили, обладает лазерное излучение. Однако, получение интерферограмм в лазерном свете имеет свои недостатки, поэтому часто в микроинтерферометрах используют обычные (тепловые) монохроматические источники излучения с малой когерентностью. Это приводит к необходимости очень точно выравнивать оптическую длину пути опорного и сигнального каналов, чтобы уменьшить разность фаз между ними. Для этого в приборах используют специальные оптические компенсаторы.
Оптических схем интерференционных микроскопов, использующих описанные принципы, разработано много. Мы остановимся только на трех схемах, которые дают принципиально разные результаты. Это микроскоп Лейтца, дифференциальные интерференционные или ширинг-системы и микроскоп Линника. Большинство экспериментальных результатов в нашей книге получено на последнем микроскопе, поэтому его схему мы подробно опишем в следующем разделе, а здесь остановимся на первых двух.
В ширинг (сдвиговых) микроскопах (рисунок. 7.16) разделение и сведение лучей осуществляется двояко преломляющими элементами - кристаллическими пластинами.
Рисунок. 7.16
Как правило, в качестве них используют призмы Волластона 3 и 7. Оптическое излучение от источника 1 проходит через поляризатор 2 и направляется на призму 3, в которой происходит разделение лучей в направлении перпендикулярном оптической оси. Затем оба луча, поляризованных в двух взаимно перпендикулярных направлениях, при помощи конденсора 4 направляются на препарат 5. Через него проходят оба луча, но каждый через свою область препарата. При этом стараются так выбрать зону наблюдения, чтобы в одной области был микрообъект, а другая была без него. Микрообъектив 6 и вторая призма 7 совмещают оба изображения на регистраторе 8, где наблюдается интерференционная картина. Сдвиг между изображениями, т.е. расстояния между зонами наблюдения на препарате может составлять от 20 до 100 микрон, в зависимости от типа прибора и микрообъектива. Очевидны недостатки данной схемы. Во-первых, достаточно трудно выбрать область наблюдения на препарате, т.к. нужно найти изолированную клетку в окружении достаточно однородного фона. Во вторых, практически невозможно автоматизировать процесс расшифровки интерфереграмм.
Своеобразное решение первой задачи нашел Номарский, который предложил дифференциальный интерференционный контраст (ДИК). В его схеме смещение между сигнальным и опорным пучками выбирается близким к разрешающей способности микроскопа, т.е. очень малое. При этом не наблюдается двоения изображения, а происходит сравнение фаз в двух соседних точках волнового фронта, прошедшего через объект. Это эквивалентно дифференцированию распределения фазы. Отсюда и название метода. Уравнение описывающее интерферограмму в данном случае имеет вид:
![]() (7.21)
(7.21)
где
Dх - величина смещения между сигнальным и опорным пучками в плоскости препарата.
Предложенный метод позволяет получать прекрасные фазовые изображения.
Однако, автоматизированных методов расшифровки интерференционных картин такого типа еще не разработано.
Данный вид микроскопии применяется для исследования анизотропных сред в поляризованном свете. Как уже отмечалось, некоторые биологические объекты, например, мышечные волокна обладают свойством двулучепреломления, измерение которого позволяет определять особенности строения живых клеток. На рисунке 7.17 представлена принципиальная схема поляризационного микроскопа.
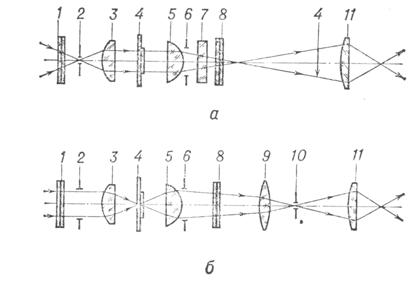
а – для ортоскопического наблюдения; б – для коноскопического наблюдения;
1- поляризатор; 2, 6 – диафрагмы; 3- конденсор; 4 – препарат; 5 – объектив; 7 – компенсатор;8 – анализатор;9 – линза Бертрана; 10- фокальная плоскость окуляра; 11- окуляр.
Рисунок 7.17 –Принципиальная схема поляризационного микроскопа
При ортоскопическом ходе лучей (рисунок 7.17, а) в фокальную плоскость окуляра 11 проецируется изображение 4' препарата 4. Наблюдаемая при этом интерференция поляризованых лучей локализована в плоскости препарата. Пучок лучей, прошедших через поляризатор 1, ограничивается апертурной диафрагмой 2 конденсора 3 с помощью поворотного анализатора 8 и компенсаторов различных типов 7 производится измерение величины двойного лучепреломления, углов поворота плоскости поляризации, определение углов погасания поляризации других характеристик. При коноскопическом ходе лучей (рис. 7.17, б) апертурная диафрагма 2 открывается, а наблюдение интерференционной картины, локализованной в бесконечности, производится с помощью линзы Бертрана 9, которая проецирует выходной зрачок 6 в фокальную плоскость 10 окуляра. Получаемые при этом изображения дают возможность определить знак двойного лучепреломления, количество осей объекта, их ориентацию и величину угла между осями.
Современные поляризационные приставки к микроскопам позволяют измерять разность фаз, вызванных двойным лучепреломлением с точностью l/ 100 по всему полю зрения.
Одним из самых быстроразвивающихся направлений в современной оптической микроскопии (включая конфокальную, многофотонную и ближнего поля) является флуоресцентная микроскопия. Данный вид микроскопии использует для формирования изображения оптическое излучение, возникшее внутри микрообъекта в результате явления фотолюминисценции. Можно выделить два механизма возникновения такого рода излучения
1.Собственное свечение веществ, входящих в состав клетки, которое возникает после возбуждения ее внешним излучением определенной длины волны. Это называется самофлуоресценцией, Примером такого явления может служить
2.Свечение веществ специально введенных в клетку, под действием внешнего оптического излучения определенной длины волны. Это явление называется вторичная люминесценция. В качестве такого рода веществ может применятся химический или биологический препарат, который избирательно связывается с веществами внутри клетки и вызывает их свечение, он называется флуоресцентным зондом или флуорофором. Примером такой микроскопии является
Флуоресцентный микроскоп должен отвечать следующим требованиям:
- возбуждение флуоресценции в препарате должно быть эффективным и желательно, чтобы оно происходило на частоте оптического излучения близкой максимальной частоте поглощения света флурофором, т.е. освещение препарата должно осуществляться на строго определенной длине волны.
- микроскоп должен собирать как можно больше света при флуоресценции, при этом постороннее излучение приводит к образованию нежелательного фона в изображении.
Вторичное оптическое излучение имеет длину волны отличную, как правило большую, от длины волны излучения, возбуждающего объект. Поэтому оптическая схема флуоресцентного микроскопа отличается от обычного наличием двух светофильтров. Первый находится в осветительной системе и выделяет из всего спектра источника освещения объекта возбуждающее излучение требуемой длины волны. Второй, расположенный после микрообъектива, пропускает только свет флуоресценции, поглощая возбуждающее излучение. Как правило, использование флуоресцентного метода предполагает использование микроскопа в котором оптическая система монтируется за образцом так, что область над образцом легко доступна для манипуляций.
. Исследователь выбирает тот флуорофор, который наиболее четко и ярко способен выделить интересующую его область. Существуют зонды флуоресцирующие только в присутствии кальция, калия, натрия. С использованием таких зондов, например, по уровню флуоресценции в присутствии кальция можно оценить активность клетки. Число потенциально используемых флуорофоров насчитывает тысячи и постоянно увеличивается.
Основной недостаток данного метода в том, что введение постороннего химического вещества в клетку может изменить ее химический состав и нарушить сбалансированную работу ее отдельных компонентов. При этом иногда трудно оценить степень данного влияния. Другой недостаток в том, что трудно произвести количественную интерпретацию получаемых данных. В настоящее время этот метод микроскопии развивается наиболее быстро и является очень перспективным для исследования процессов происходящих в живых клетках.
“Обычные оптические световые микроскопы столь важное средство для исследований, что они не устарели ”,- утверждает менеджер компании Leica Inc. Эти микроскопы все еще широко применяются, так как они сравнительно не дороги, просты в использовании и надежны для повседневных, рутинных исследований, составляющих основу любой научной работы.
Несмотря на то, что оптическая конструкция микроскопов не изменилась, разработчики сделали акцент на улучшение качества используемой оптики, а также на простоту эксплуатации. Недавно многие крупные компании представили конструкции микроскопов с ручным и компьютерным управлением.
Претерпел изменение и внешний дизайн микроскопа: он рассчитан на максимальное удобство при длительном использовании. Новое расположение ручек управления (например, фокусировки) не приводит к сильному напряжению рук исследователя и они (ручки) могут быть легко найдены даже в затемненном помещении. Наклон окуляра изменяется, что удобно при работе разных пользователей – высоких и низких.
Новое направление в микроскопии – применение “инфинитной” оптики. При использовании “финитной” оптики расположение объектива и окуляра определяется конечными размерами тубуса микроскопа так, что лучи собираемые объективом должны быть сфокусированы в центре диафрагмы окуляра. Основная проблема заключается в том, что введение новых оптических элементов в тубус требует корректировки пути луча так, чтобы свет фокусировался на диафрагме окуляра, а это в свою очередь приводит к появлению дисторсии и другим нежелательным эффектам. Решением было создание области за объективом, в которой лучи идут параллельно друг другу. Эта область, названная как “инфинитная”, позволяет использование дополнительных оптических элементов, введение которых не приводит к искажению изображения исследуемого объекта.
Вместе с использованием “инфинитной” оптики, улучшилась конструкция и качество материала линз. Крупные производители микроскопов заявляют, что достижение наилучших результатов при использовании “инфинитной” оптики во многом определяется выбором конструкции микроскопа, а также использованием широкого ряда дополнительных средств, разработанных специально для данного микроскопа. Такое быстрое освоение компаниями новых видов техники и отказ от производства старой приводит к тому, что те кто купили микроскоп буквально три года назад не могут достать к нему запчастей. Особенно сильной критике подвергается компания Nikon Inc. которая переделала выпускаемые микроскопы столь радикально, что новые и старые микроскопы не совместимы. Менеджер по продажам этой компании сказал, что целью этого было улучшение качества изображения и функциональных возможностей данных микроскопов, за счет увеличения длины тубуса до 200 мм и диаметра до 60 мм. “Мы уверены, что новая конструкция позволит сделать высококачественный микроскоп более доступным”,- заявил он.
Еще одна важная проблема, представляющая интерес для многих исследователей – проблема совместимости. В 1857 году Британское Королевское Общество по микроскопии представило промышленные стандарты для выпуска микроскопов, а к середине 20-го века они стали общими для многих фирм и способствовали некоторой взаимозаменяемости выпускаемых компонентов. Например, в течении ряда лет объективы фирмы Carl Zeiss подходили для микроскопов фирмы Leica и наоборот. Сейчас новые оптические схемы столь разнообразны, что их компоненты уже давно не взаимозаменяемы.
Отсутствие совместимости между микроскопами разных фирм - результат индивидуальности подходов каждой из них к созданию высококачественной оптики. Несмотря на “неклассические” подходы в создании новых оптических систем, имеющих поразительно высокое разрешение, обычные световые микроскопы все еще занимают лидирующее место и остаются главным рабочим средством во многих областях. Кроме традиционного применения в биологии, они используются и во многих других исследованиях.
Необходимость в автоматизации процесса исследования биологических объектов, осуществляемых микроскопами, сейчас не вызывает никаких сомнений. Практически все фирмы, занимающиеся выпуском оптических микроскопов, предлагают полный набор систем автоматического сбора данных и различных пакетов программ обработки. Применение автоматизации обусловлено двумя обстоятельствами. Во-первых, широким распространением персональных компьютеров, которые вошли в рутинную практику врачей лаборантов и исследователей. Во-вторых, применением обычных, достаточно дешевых видеокамер на ПЗС (прибор с зарядовой связью) или по-английски - CCD структурах для визуализации изображений на экране телевизора в традиционных микроскопах, с последующим вводом этих изображений в персональный компьютер.
Принцип ее действия достаточно прост и понятен из рисунка. Изображение препарата формируется микроскопом в плоскости приемного элемента телекамеры, регистрируется им и преобразуется в телевизионный электрический сигнал. При необходимости этот сигнал может быть записан на видеомагнитофон, отображен на экране телевизора и т.д. Для ввода изображения в компьютер используется специальная плата стыковки (frame grabber), которая преобразует телевизионный сигнал в набор чисел. Характеристики всей системы анализа изображения можно разделить на технические и программные. Технические возможности системы регистрации и ввода изображений в компьютер определяются характеристиками телекамеры. В настоящее время наибольшее распространение получили телекамеры, удовлетворяющие телевизионному стандарту:
- число элементов разложения в изображении 700х450
- число градаций яркости для черно-белого изображения 256
- время регистрации изображения 1/25 секунды.
Очень важной характеристикой телекамеры является ее чувствительность, т.к. именно эта характеристика определяет силу света источника освещения препарата. Особенно данная характеристика важна для флюоресцентной микроскопии, когда свечение объекта невелико. Чувствительность телекамеры указывается в ее паспортных данных.
Заметим, что развитие микроэлектроники идет достаточно быстрыми темпами, поэтому технические характеристики телекамер все время улучшаются.
Программные возможности современных систем компьютерной обработки изображений микрообъектов достаточно велики. Они содержат большой пакет прикладных программ рутинной обработки изображений микрообъектов. Эти программы работают, как правило, в интерактивном режиме, т.е. требуют присутствия оператора. Каждая фирма , производящая автоматизированные микроскопы, снабженные системой обработки изображений, обычно использует собственное программное обеспечение, имеющие свои особенности и возможности. Тем ни менее, нетрудно классифицировать и выделить общие направления в обработке изображений микрообъектов, которые присущи практически всем современным системам, и тот класс задач, решение которых обеспечивается этими программными комплексами.
Оптическая плотность клетки и ее органел может быть измерена путем сравнения количества света прошедшего через части клетки и прошедшего через чистое поле. С помощью телекамеры и программного обеспечение мы получаем величину светового потока, прошедшего через клетку, в виде чисел от 0 до 255. Это не абсолютное значение величины светового потока, а относительная величина. Для того, чтобы измерять абсолютную величину светового потока необходимо провести калибровку и получить кривую по которой пересчитывается величина яркости в абсолютное значение светового потока. Необходимо отметить, что для проведения денситометрических измерений необходима калибровка всего комплекса. Для того чтобы обеспечить воспроизводимость и достоверность результатов необходимо составление специальной методики по калибровке и проведению измерений. Методика должна включат в себя правила регулировки и выбора параметров всех узлов комплекса, включая микроскоп, телекамеру, плату ввода изображений и программу.
Колориметрия - это измерение цветовых характеристик на изображении. Если диагностика строится на основе анализа цвета и оттенков цветов клеток и тканей, то без измерения цветовых характеристик трудно поставить точный диагноз. Компьютерная обработка может с большой точностью определять цветовые характеристики изображения, и это может стать основой для более постановки диагноза. При работе с цветными изображениями возможны два варианта - ввод изображения с помощью цветной или черно/белой телевизионной камеры. Удобство работы с цветной камеры состоит в том. что видно сразу все цвета в изображении. Применение цветной телекамеры позволяет провести простой спектральный анализ в трех спектральных областях - красной, зеленой и синей, так как цветное изображение состоит из трех соответствующих изображений. Недостаток цветных камер - низкая чувствительность. Так, в частности, для анализа флюоресцентных объектов, которые излучают различные длины волн, у обычных цветных камер не нахватает чувствительности для регистрации и ввода в компьютер их изображений. При работе с флуоресценцией необходимы специальные цветные телекамеры, работающие в режиме накопления, которые достаточно дороги. При использовании черно/белых камер чувствительности хватает. Для того, чтобы синтезировать в компьютере цветное изображение при помощи черно-белой камеры достаточно получить три моноцветных изображения, пропуская излучение от объекта последовательно через красный, синий и зеленый светофильтры. Для более точного спектрального анализа изображений используются интерференционные фильтры. Они пропускают очень узкий диапазон длин волн оптического излучения, что позволяет получить набор одноцветных изображений в различном спектральном диапазоне. При этом с помощью подбора фильтров можно выделить любое количество спектральных линий в области спектральной чувствительности телекамеры - от 0. 4 мкм до 1 мкм. Как правило используют до 10 фильтров.
Необходимо подчеркнуть, что в обоих случаях речь не идет об абсолютных измерениях цветовых и спектральных характеристиках изображений. Возможно определение только соотношений в интенсивности различных цветов, т.е. относительные измерения. Переход к абсолютным измерениям возможен только при соответствующей калибровке и аттестации прибора. Эта процедура длительная и дорогостоящая и применяется для серийных приборов крайне редко.
Наиболее широко применяются программы, которые позволяют проводить измерения размеров объектов с высокой точностью. Наиболее часто измеряемыми параметрами являются следующие:
- площадь клетки или ядра клетки
- периметр клетки
- линейные размеры
- коэффициент вытянутости ( отношение двух главных моментов)
- коэффициент формы ( степень отличия от круга)
- отношение площади ядра клетки к площади цитоплазмы
Существует два основных способа измерения признаков - ручной и автоматический. При ручном режиме измерения пользователь с помощью мышки обводит на изображении необходимую клетку, и программа автоматически измеряет все необходимые признаки для данной клетки. При автоматических измерениях программы с помощью пороговой обработки автоматически выделяет все объекты на изображении а затем для всех выделенных объектов рассчитывает значения необходимых признаков. Автоматические измерения применимы не всегда. Обычно автоматические измерения эффективны для анализа простых частиц (клеток) четко выделяющихся от фона. В случае обработки гистологических препаратов, когда границы клеток не являются резко выраженными, обычно удобнее пользоваться ручными методами измерения
Программы анализа изображений включают в себя процедуры для подсчета количества клеток в поле зрения микроскопа. Кроме подсчета программа может для каждой клетки вычислить необходимые морфологические признаки. Итогом работы программы является построение гистограммы распределения клеток по необходимому признаку. Например распределение клеток по площади. Кроме этого программа может рассортировать клетки по классам. Например, если клетки разных классов различаются по площади, то можно подсчитать количество больших и количество маленьких клеток. В тех случаях когда количество клеток в поле зрения превышает несколько десятков, то подсчет становится затруднительным и неточным.
Все перечисленные программы можно отнести к рутинным. Составление их не представляет большой сложности, а их отличия заключаются лишь в оболочке и в большей или меньшей степени проработке сервисных функций.
Гораздо больший интерес представляют системы эвристической обработки изображений. Это в первую очередь программы, использующие алгоритмы распознавания образов. Построение системы автоматизированной обработки изображений клеток, включающей в себя их распознавание, представляет собой сложную задачу, которая требует объединения усилий биологов и врачей с одной стороны и математиков-программистов с другой.
Особенностью методов распознавания является то, что невозможно подобрать единый алгоритм для анализа изображений различных типов. Поиск информационных признаков для каждого класса образов, выбор решающего правила и т.д. представляет собой в каждом конкретном случае очень интересную и творческую задачу. Современные достижения в области информатики и большой опыт в решении подобных задач, оставленный нам от оборонных разработок, даёт уверенность в скором появлении систем распознавания и обработки изображений клеток различных типов.
Характерной чертой современной оптической микроскопии является стремление к увеличению получаемой информации об объекте исследования. В связи с этим развиваются различные области микроскопии. И одним из таких направлений является 3D-микроскопия. Основная задача, которую она решает – получение информации о пространственном распределении некоторого параметра исследуемого объекта: показателя преломления, коэффициента абсорбции, коэффициента рассеяния, распределения флуоресцентных меток и пр.
Методы 3D микроскопии можно классифицировать по принципу получения информации о внутренней структуре:
- без численной реконструкции, чисто аппаратными средствами;
- с использованием численной реконструкции по результатам измерений.
Основными представителями первого направления являются конфокальная микроскопия и оптическая когерентная микроскопия. Принципы конфокальной микроскопии были заложены профессором Марвином Мински в 50-х годах 20-го столетия.
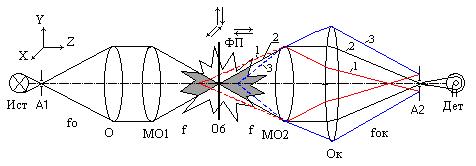
Рисунок 7.18 – Принцип работы конфокального микроскопа в проходящем свете.
В основе получения оптических срезов исследуемого объекта с помощью конфокального микроскопа лежит принцип пространственной фильтрации и двумерного сканирования. На рисунке 7.18. представлена оптическая схема конфокального микроскопа для проходящего света. Прошедшее, отраженное или испускаемое объектом (Об) излучение проходит через микрообъектив (МО2) в точечную диафрагму – пинхол (А2). При этом пропускается только излучение 2 от малой области (точки) узкого слоя лежащего в фокальной плоскости (ФП) микрообъектива МО2, излучение же 1 и 3 от других точек отсекается диафрагмой (А2). Для визуализации отдельных сечений объекта, микроскоп производит сканирование, либо путем перемещения объекта (по плоскости XY и вдоль Z) (см.рисунок 7.18) – scanning stage, либо перемещения луча (см.рисунок 7.19) – scanning beam, и в том и в другом случае изображение получается попиксельно. Произведя запись многих слоев объекта возможно дальнейшее получение его трехмерного изображения.
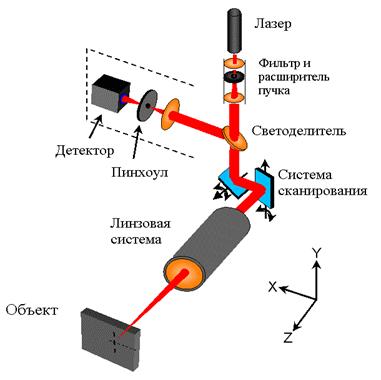
Рисунок 7.19 – Конструкция конфокального микроскопа на отражение.
Такое трехмерное изображение является не трехмерной томограммой, а трехмерным суммарным изображением. Поэтому без использования принципов реконструкции конфокальный микроскоп не может быть томографическим.
В основе оптического когерентного микроскопа, основанного на принципах оптической когерентной томографии, лежит особенность интерференции низкокогерентного источника. На рисунке 7.20 представлена оптическая схема такого томографа.
Принцип действия такого микроскопа заключается в интерференции опорного пучка и рассеянного в тонком слое внутри объекта предметного пучка. Толщина слоя определяется длинной когерентности источника. Сканирование вдоль оптической оси опорного пучка позволяет получать набор слоев, из которых формируется трехмерное изображение.

Рисунок 7.20 – Оптическая схема оптического когерентного томографа.
В данном случае получение изображений внутренних сечений также производится аппаратными средствами без использования реконструкции, поэтому они не являются томограммами.
Изначально задача получения изображений внутренних сечений 3D объектов в оптике и, в частности, в микроскопии не формулировалась как томографическая. Однако в самой постановке такой задачи скрыто слово томография, т.к. это изображение сечения и есть томограмма (от греческого слова tomos – слой).
Создание компьютерного оптического микротомографа, основанного на реконструкции томограмм, требует решения сложной научно-технической задачи встраивания в микроскоп системы сбора проекционных данных. Схемы зондирования можно разделить на следующие классы:
1. с поворотом пучка зондирующего излучения относительно неподвижного объекта;
2. с вращением (наклоном) объекта относительно неподвижного пучка зондирующего излучения.
Рассмотрим основные подходы к организации многоракурсного зондирования в схемах с неподвижным объектом.
Для получения проекционных данных использовалась внеосевая вращающаяся точечная диафрагма. Это одна из первых работ, в которой микроскоп использовался как томограф. Однако он был пригоден только для исследования флуоресцентных объектов. Траектория зондирования «экватор».
Схема со смещением точечного источника в плоскости апертурной диафрагмы конденсора и получение наклонного освещения за счет поворота зеркала представлена на рисунке 7.23,а.. Недостаток схемы в одномерности траектории сканирования. На рис. 7.21 представлена оптическая схема такого микроскопа.
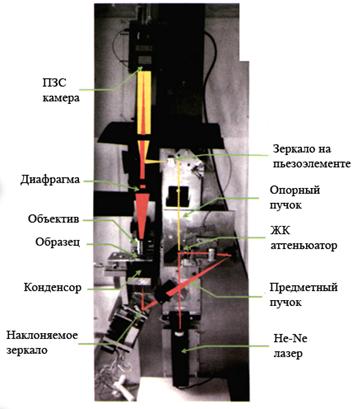
Рисунок 7.21 – Оптическая схема томографического микроскопа
Другой подход основан на использовании матрицы микрозеркал DMD (Digital Micromirror Devices) (рис.7.22), помещенных в плоскости апертурной диафрагме микрообъектива (рис. 1.23,б), которые используются для создания наклонного освещения. Схема может быть применена только для небольших объектов и имеет малый угол зондирования – 20º. Траектория зондирования – любая двумерная (2D).
Использование двумерного смещения точечного источника в плоскости апертурной диафрагмы микрообъектива и получение наклонного освещения представлено на рисунке 1.23,в. Траектория зондирования – любая двумерная (2D).

Рисунок 7.22 – Матрица микрозеркал DMD (Digital Micromirror Devices) обеспечивает угол зондирования 20º
|
|
||||
| а |
б |
в |
г |
д |
a-в) со сканированием пучка зондирующего излучения относительно неподвижного объекта;
г, д) с движением объекта относительно неподвижного пучка зондирующего излучения.
1, 5 – передняя и задняя фокальные плоскости микрообъективов, 2, 4 – микрообъективы, 3 – объект, 6 – источник, 7 - держатель.
Рисунок 7.23 – Схемы зондирования объекта в микроскопии
Схемы со сканированием объекта относительно неподвижного пучка (axial microtomography) реализованы для следующих вариантов вращения:
1. вращение капилляра с находящимся внутри него объектом;
2. наклон объекта, помещенного между двумя покровными стеклами (рисунок 7.23, г).
Схема с вращением капилляра обеспечивает большой угол зондирования, однако имеет недостатки, связанные с изготовлением тонкостенного капилляра, размещением в нем единичного объекта, подбор иммерсионных сред для выравнивания показателей преломления, дефокусировкой изображения и пр.
Рассмотрим схему с вращением объектов помещенных на поверхность оптоволокна. Здесь был использован тот факт, что при вращении волокно не смещается относительно своей оси. Однако эта техника требует создания специальных алгоритмов для выравнивания проекций с учетом переналожения изображений разных объектов друг на друга.
Общий недостаток всех схем, использующих вращение – дефокусировка изображения. Возможный выход - замена вращения на плоско-параллельное движение объекта в широком конусном пучке, рисунок 7.23,д . Такое движение не приводит к выходу из области фокуса. Особенности данной схемы описаны в главе 4 диссертационной работы.
Использование оптического микроскопа в качестве микротомографа накладывает определенные ограничения на схему сбора проекционных данных. Эти ограничения связаны с уменьшением угла обзора и размерности траектории сканирования.
Для схем с неподвижным объектом угол обзора определяется числовой апертурой используемого микрообъектива и, как правило, не превышает ±45º. Исключение составляет схема с вращающимся капилляром, в которой угол зондирования лежит в пределах ±90º. В микроскопе практически невозможно обеспечить угол зондирования равный 90º. Но его можно сделать близким к 90º, например, использовав иммерсионные микрообъективы.
Методы реконструкции, используемые в современной томографии можно классифицировать следующим образом:
1. алгоритмы, основанные на формулах интегральной геометрии;
2. алгебраические методы;
3. методы фурье.
Для реконструкции томограмм в условиях ограниченного угла наиболее адекватными являются итерационные алгоритмы, основанные на использовании алгебраических методов и фурье-методов.
Ограниченный угол зондирования уменьшает точность реконструкции, поэтому особые требования предъявляются к траектории сбора проекционных данных. Для реконструкции были выбраны следующие алгоритмы: алгебраический ART (Algebraic Reconstruction Technique) и комбинированный сART (комбинация ART с методами фурье). В качестве области реконструкции рассматривался единичный шар. На описывающем его кубе была задана сетка 65´65´65 узлов. Проекции задавались на сетке 65´65 узлов.
Восстановление велось по 21-ой проекции. Предполагалось, что проекции получены в угловом диапазоне 80° по азимутальному углу j и столько же по полярному углу q. Были рассмотрены различные возможности размещения 21-ой проекции в этих пределах, которые были условно названы «экватор», «крест» и «квадрат» (рис. 7.24). Траектория «экватор» : все проекции имели q=90°, а по углу j были равномерно (через 4°) распределены в диапазоне [-40°; 40°] (рис. 7.24,а). Траектория «крест» 11 проекций расположены по экватору через 8° в диапазоне [-40°; 40°], остальные таким же образом расположены по меридиану, для них j=0°, qÎ[50°; 130°]. Траектория «квадрат» с равномерным распределением проекций по q и по j.
|
|
|
| а |
б |
в |
q. а - траектория «экватор»; б- траектория «крест» в- траектория «квадрат»
Рисунок 7.24 – Траектории зондирования в условии ограниченности угла
Результаты моделирования показали, что ошибка реконструкция при ограниченном угле зондирования коррелирует с траекторией сканирования. Она минимальна, когда траектория сканирования двумерна (2D), а получающиеся проекции равномерно распределены по сетке.
Таким образом, тенденции современных интерференционных измерений интегральных параметров фазовых микрообъектов (фазовых изображений и вычисляемых по ним характеристик) требуют обеспечения высокоточных автоматизированных измерений при большой разрешающей способности и чувствительности. Для обеспечения данных требований был разработан и прошел экспериментальную проверку автоматизированный интерференционный микроскоп на базе микроскопа Линника. Требования к высокой точности, чувствительности и разрешающей способности относятся и к измерению локальных параметров фазовых микрообъектов, так как проекции, по которым эти параметры вычисляются, являются фазовыми изображениями. Дополнительными являются требования на траекторию сканирования, которая должна обеспечивать равномерное распределение проекций на двумерной сетке («квадрат»), и на угол зондирования, который должен быть максимален (близок к 90°). В связи с этим, были разработаны и экспериментально опробованы оптические схемы интерференционных микротомографов на основе микроскопа Линника, на основе конфокального микроскопа, обеспечивающие двумерную траекторию сканирования типа «квадрат», а также интерференционный микротомограф с зеркальным иммерсионным конденсором, имеющим большой угол зондирования (±63°).
В отечественной промышленности широко известен микроинтерферометр МИИ-4. Этот микроинтерферометр серийно выпускается предприятием ЛОМО (Санкт-Петербург) и предназначен для визуальной оценки и измерения параметров шероховатости отражающих объектов. Принцип и схема микроинтерферометра МИИ-4 впервые были разработаны и применены для исследования качества тонкообработанных поверхностей академиком В. П. Линником.
К основным его недостаткам относятся: сложности работы и настройки в белом и квазимонохроматическом свете, отсутствие видеорегистрации изображений, расшифровка интерферограмм производится оператором вручную. Это накладывает известные ограничения на точность и время измерений.
Данный прибор лег в основу автоматизированного интерференционного микроскопа (далее автоматизированного микроскопа).
В МИИ-4 реализована схема инвертированного микроскопа, при этом исследуемый объект располагается на зеркале и излучение дважды проходит через него, что вдвое повышает чувствительность измерения ОРХ по сравнению со схемами «на просвет», когда излучение проходит через объект один раз.
Важным достоинством интерферометра Линника является возможность работы с широким источником пространственно-некогерентного монохроматического излучения. Это приводит к значительному уменьшению когерентных шумов и улучшению, по сравнению с интерферометрами с точечными источниками света, качества получаемых изображений.
Использование широкого источника в микроскопе Линника определяет особенности формирования и локализации интерференционной картины, которые рассмотрены далее.
Принципиальная оптическая схема микроскопа, построенного по схеме Линника, с протяженным источником пространственно-некогерентного квазимонохроматического света, приведена на рисунке 7.25.
Микроскоп состоит из двух идентичных ветвей: предметной 3-4-5-6-7 и опорной 3-8-9-10. Каждая из них в прямом ходе лучей представляет собой широко известную в микроскопии оптическую схему освещения объекта по Кёлеру. В обратном ходе лучей эти ветви вместе с линзой 11 позволяют сформировать изображение объекта 6 и зеркал 7, 10 в выходной плоскости 12 и одновременно получить две системы волн, способных интерферировать, т.к. они образуются делением пучка лучей, исходящих из одной точки протяженного источника света. Здесь и далее везде считается, что используемое излучение является квазимонохроматическим, т.е. спектральная полоса этого излучения мала по сравнению со средней частотой.
В отличие от обычного микроскопа Линника в представленной схеме линза 11 расположена на фокусном расстоянии от плоскостей 4, 8 так, что микрообъективы 5, 9 образуют с ней телескопическую (конфокальную) пару. Это условие необходимо для того, чтобы изображения различных продольных плоскостей объекта 6 имели одинаковый масштаб. Только при таком расположении линзы 11 отображающая система микроскопа будет инвариантна к сдвигу вдоль оптической оси.
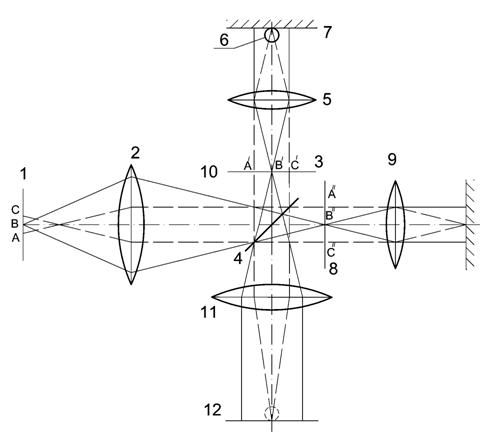
1 – протяженный источник света; 2, 11 – линзы; 3 – светоделитель; 4, 8 – передние фокальные плоскости микрообъективов; 5, 9 – микрообъективы; 6 – объект; 7, 10 –предметное и опорное зеркала; 12 – выходная плоскость.
Рисунок 7.25 – Оптическая схема интерференционного микроскопа с пространственно-некогерентным источником света по схеме Линника
Протяженный источник света 1 рассматривается как совокупность некогерентных друг с другом точечных квазимонохроматических источников оптического излучения. Рассмотрим некоторые из них, например, А, В, С на рис.1.7. Пусть источник В находится на оптической оси, а источники А и С на некотором расстоянии от нее в поперечном направлении. Покажем, что каждый такой источник создает свою собственную интерференционную картину, вид которой зависит от его положения относительно оптической оси.
Проследим вначале за ходом лучей (сплошные линии на рисунке 7.25), которые участвуют в формировании интерференционной картины, только от источника В. Линза 2 расположена так, что строит изображение источника В и всей плоскости 1 в передних фокальных плоскостях 4, 8 микрообъективов 5, 9. Поэтому объект 6 и зеркала 7, 10 освещаются параллельными пучками. Отраженное от зеркал 7, 10 излучение распространяется в обратном направлении и после светоделителя 3 во всей области перекрытия пучков опорного и предметного каналов создается интерференционная картина. Если нормаль к зеркалу 10 опорного канала расположена под небольшим углом к оптической оси, а зеркало 7 предметного канала перпендикулярно оптической оси, то формируется интерферограмма в полосах конечной ширины. Частота полос определяется относительным углом наклона зеркал 7 и 10. Искривление полос зависит от формы волнового фронта предметного пучка света, прошедшего дважды в прямом и обратном ходе через фазовый объект 6. Таким образом, картина интерференции от одного точечного источника локализована (контрастна) во всей области пересечения предметного и опорного пучков света.
Ход лучей при формировании интерференционных картин от других точечных источников, смещенных относительно оптической оси в поперечном направлении, например, в точку А, аналогичен только что рассмотренному. Поэтому на рисунке 7.25 приведены пунктирными линиями лишь оси пучков света от этих источников, а на рисунке 7.26 изображена более детально часть схемы освещения объекта 6.
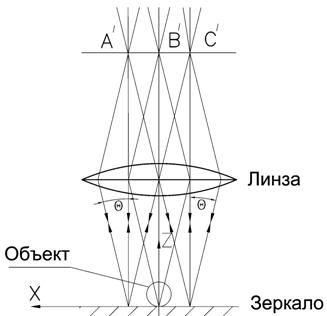
Рисунок 7.26 – Схема прохождения лучей через фазовый объект в микроскопе Линника.
Из рисунков 7.25, 7.26 следует, что от точечного источника А после микрообъективов 5, 9 распространяются уже наклонные к оптической оси параллельные пучки света. В отличие от предыдущего случая, теперь объект 6 зондируется плоским пучком света не по нормали, а под некоторым углом q. Угол наклона q зависит от расстояния АВ и, соответственно, А1В1. Максимальный угол наклона определяется числовой апертурой микрообъективов 5, 9 и размером объекта 6. Причем объект 6 должен весь находиться в области пересечения этих пучков. Из рис. 2.1 видно, что размер этой области зависит от положения зеркала 7 и достигает своего наибольшего значения при размещении его точно в задней фокальной плоскости микрообъектива 5. Соответственно, зеркало 10 опорного канала также должно находится в задней фокальной плоскости микрообъектива 9. Отраженное от зеркал 7, 10 и светоделителя 3 излучение идет под небольшим углом друг к другу из-за относительного наклона этих зеркал. Этот угол определяет частоту полос в интерференционной картине. Далее излучение преобразуется линзой 11 в параллельные пучки и направляется под некоторым углом к оптической оси в выходную плоскость 12, причем этот угол определяется удаленностью точечного источника от оптической оси. Так как эта пара пучков образована из одного точечного источника А, то они когерентны и при регистрации в любой плоскости в пространстве изображений микроскопа создают свою нелокализованную интерференционную картину. Частота полос в этой картине будет такая же как и для точечного источника В, но форма искривления полос будет другая, т.к. предметный пучок света проходит через объект 6 под углом, т.е. по другому пути. Аналогично описывается образование интерференционных картин для любого другого точечного источника.
В пространстве изображений формируется непрерывный набор из пар когерентных волновых полей (предметного и опорного). Каждая такая пара волн создает при регистрации свою собственную интерферограмму. Область локализации такой интерференционной картины совпадает с областью пересечения каждой пары предметного и опорного пучков. Частота и ориентация полос у всех интерферограмм одинакова, т.к. она определяется относительным наклоном зеркал 7, 10. Однако форма искривления полос несколько отличается друг от друга, т.к. предметные пучки света проходят разные пути в объекте 6 из-за различного угла зондирования.
При настройке микроскопа, например, на полосы конечной ширины, перпендикулярные оси x, уравнение элементарной интерферограммы можно записать в виде:
|
|
(7.22) |
где a - угол между предметным и опорным пучками для данного положения точечного источника. Здесь предполагается, что интенсивность обоих этих пучков одинакова и равна i’.
Так как точечные источники некогерентны между собой, то интерферограмма I(x,y) для протяженного источника света будет формироваться как сумма элементарных интерферограмм (7.22). Для непрерывного набора источников можно записать:
|
|
(7.23) |
Область интегрирования в (7.23) определяется угловыми размерами источника. Для широкого источника, заполняющего всю апертуру микрообъектива 5, она зависит от его числовой апертуры.
Таким образом, изображение, формируемое в микроскопе Линника с пространственно-некогерентным источником света, является суммой интерферограмм волновых полей, исходящих из различных точек источника, поэтому контрастная интерференционная картина наблюдается в плоскости изображения предметного и опорного зеркал.
Следует отметить, что это свойство значительно улучшает качество интерференционной картины, получаемой на микроскопе Линника, так как суммирование уменьшает шумы источника.
Использование широкого источника в микроскопе Линника приводит к локализации интерференционной картины – контрастная интерференционная картина наблюдается в ограниченной области вдоль оптической оси.
Так как выходная плоскость 12 и плоскости размещения зеркал 7, 10 оптически сопряжены, то оси пучков из всего набора точечных источников, на которые условно разбит протяженный источник света 1, будут пересекаться в одной точке, лежащей в плоскости фокусировки изображения зеркал 7, 10. Таким образом, только в этой плоскости элементарные интерференционные картины от каждого точечного источника будут суммироваться без поперечного смещения. Поэтому только в данной плоскости будет наблюдаться наиболее контрастная интерференционная картина. В любой другой плоскости такие элементарные картины из-за расходимости пучков будут смещены друг относительно друга, и видность полос суммарной интерферограммы уменьшится. Это говорит о том, что область локализации интерференционных полос в микроскопе Линника с протяженным источником пространственно-некогерентного света совпадает с плоскостью 12 изображения зеркал 7, 10 предметного и опорного каналов.
Для проверки этих доводов были проведены следующие эксперименты. Исследована зависимость угла расходимости лазерного излучения на выходе из тубуса фотографического канала от диаметра диафрагмы (методом двух сечений) на микроскопе Линника МИИ-4 (ЛОМО). Было установлено, что при изменении диафрагмы от 1/1 до 1/2 угол расходимости пучка меняется в пределах от 5° до 2.8°.
Теоретически промоделирована и экспериментально исследована зависимость видности интерференционных полос при различном диаметре диафрагмы и дефокусировки, определяемой смещением объектива предметного канала. Диафрагма изменялась от 1/1 до 1/2. Шаг смещения объектива был равен одному делению микрометрического винта и составлял 3 мкм. С помощью системы ввода изображения (ПЗС камеры и платы ввода) было зарегистрировано по 11 интерференционных изображений на каждое значение диафрагмы. Первое изображение имело наибольший контраст интерференционных полос (рис. 7.27 а,б).
|
|
|
| а |
б |
а- z=0 мкм (в фокусе),
б- z=30 мкм;
D=1/1;
поле зрения 30x23 мкм.
Рисунок 7.27 – Интерференционные изображения в микроскопе Линника при различной дефокусировке
В одномерном случае, при дефокусировке на величину z один из волновых фронтов (луч 1) приобретает дополнительную разность хода ![]() , относительно другого (лучи 1¢ и 2) (рис. 7.28) и интенсивность интерференционной картины i в плоскости регистрации при равных интенсивностях предметного и опорного каналов i¢ определяется следующим выражением:
, относительно другого (лучи 1¢ и 2) (рис. 7.28) и интенсивность интерференционной картины i в плоскости регистрации при равных интенсивностях предметного и опорного каналов i¢ определяется следующим выражением:
|
|
(7.24) |
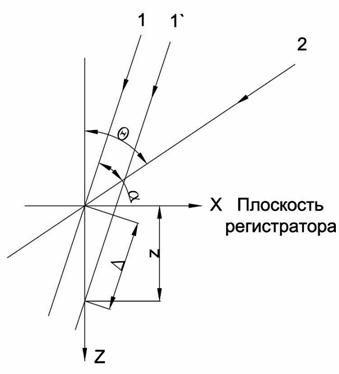
Рисунок 7.28 – К вычислению разности хода между предметным (1) и опорным (2) лучами D при дефокусировке на z.
Угол между предметным и опорным пучком a определяет ширину полосы B интерференционной картины и вычисляется по формуле:
|
|
(7.25) |
Для представленных на рисунке 7.27 интерферограмм при l=632 нм и B=6 мкм угол схождения a=3.128°.
На рисунке 7.29 а, б и в представлены теоретические (сплошная линия) и экспериментальные (точки) зависимости видности полос при различных диаметрах диафрагмы (1/1, 2/3, 1/2) и дефокусировки 30 мкм. Теоретическая интенсивность интерференционной картины вычислена по (2.1) и (2.3). Для моделирования была использована программа MathCad 11.0.
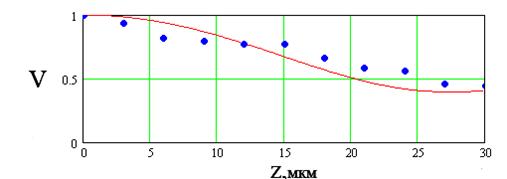
а

б
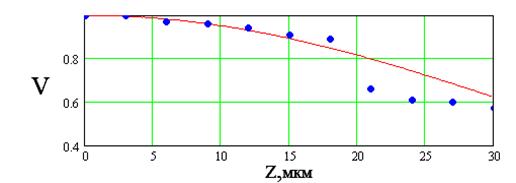
в
а- 1/1, б- 2/3, в- ½. Теоретические (сплошная линия) и экспериментальные (точки) зависимости
Рисунок 7.29 – Зависимость видности интерференционных полос V (в относительных единицах) от величины дефокусировки Z (мкм) при различных значениях диафрагмы
Из полученных результатов можно сделать следующие выводы:
1. при использовании широкого источника в микроскопе Линника наблюдается локализованная интерференционная картина. Место локализации совпадает с плоскостью, в которую отображаются предметное 7 и опорное 10 зеркала;
2. при выводе из фокуса одного из зеркал (дефокусировки) контраст интерференционной картины уменьшается;
3. уменьшение размеров источника (например, за счет изменения апертурной диафрагмы) приводит к увеличению зоны контрастной интерференционной картины.
Расшифровка интерферограмм на микроскопе Линника МИИ-4 производится вручную с помощью оператора. При этом интерференционные изображения наблюдаются визуально – через окуляр или фотографируются. По искривлению полос оценивается величина фазового сдвига, вносимого объектом. Как известно, использование ручной обработки данных носит субъективный характер и зависит от квалификации оператора. Такие измерения требуют временных затрат и не позволяют получать двумерное распределение ОРХ, а лишь ведут оценку в некоторых точках.
В настоящее время широко развиваются методы автоматизированной интерференционной микроскопии. Автоматизация измерений позволяет не только получать 2D распределение ОРХ – т.н. фазовое изображение, но и значительно увеличить точность измерения ОРХ.
Для расшифровки интерферограмм в микроскопе Линника реализован метод дискретного фазового сдвига (метод фазовых шагов). Сдвиг вносится при помощи управляемого от компьютера зеркала на пьезоэлементе (далее пьезозеркала) в опорном плече микроинтерферометра. Интерферограммы при различных положениях пьезозеркала с помощью ПЗС-телекамеры, встроенной в окулярный или фотографический канал, через плату ввода поступают в персональный компьютер (ПЭВМ), где производится их автоматическая обработка. В результате работы алгоритма реконструкции фазы восстанавливается двумерное распределение оптической разности хода (ОРХ) или фазовое изображение. Результаты измерений отображаются на экране компьютера. Для управления вводом изображений, сдвигом пьезоэлемента и расшифровки интерферограмм разработано специальное программное обеспечение для работы в операционной среде DOS «Phast» (Шумский Е., ВНИИОФИ) и среде WINDOWS «WinPhast» (Сухоруков К., Трофимов А., ВНИИОФИ).
Наличие лазерного источника освещения, имеющего значительную пространственную когерентность, приводит к образованию спекл-картины. Для подавления спекл-шума используется источник лазерного освещения с разрушителем пространственной когерентности.
Для позиционирования объекта, находящегося в поле зрения микроскопа, имеется двухкоординатный предметный стол с шаговыми двигателями, управляемый от ПЭВМ через плату управления. На рисунке 7.30. представлена блок-схема прибора.
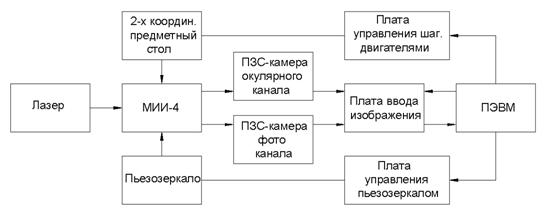
Рисунок 7.30 – Блок-схема автоматизированного микроскопа.
Функционально прибор (рис. 7.31) состоит из следующих блоков:
1. блок управления;
2. автоматизированный интерференционный микроскоп (АИМ);
3. программно-аппаратный комплекс (ПАК).
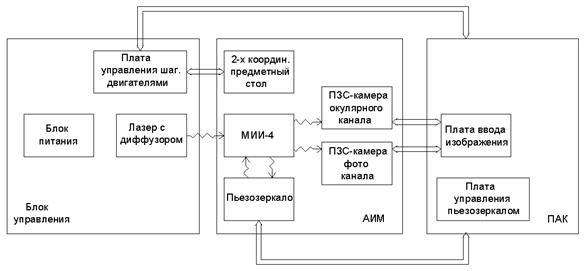
Рисунок 7.31 – Функциональная схема микроскопа. Двойная стрелка – информационная связь электрическая связь, изогнутая – оптическая связь.
Блок управления выполняет следующие функции:
- обеспечение питания составных частей прибора;
- выдача управляющих сигналов на шаговые двигатели предметного стола при управлении от компьютера;
- выдача управляющих сигналов на шаговые двигатели предметного стола при ручном управлении от кнопок;
- индикация срабатывания концевых выключателей;
- разрушение пространственной когерентности лазерного излучения;
- регулировка и контроль тока питания лазера;
- доставка излучения на АИМ с помощью волоконно-оптического жгута (на схеме рис. 7.32 не показан).
Блок управления включает в себя:
- блок питания;
- платы управления шаговыми двигателями (для каждой координаты);
- лазер с диффузором;
- волоконно-оптический жгут;
- соединительные кабели.
Оптическая схема автоматизированного микроскопа представлена на рисунке 7.32. Лазерный пучок от блока разрушителя когерентности 1,2,3 через световод 4 поступает во входной зрачок микроскопа. Выходной торец световода расположен в апертурной диафрагме, которая совпадает с передней фокальной плоскостью конденсора 5. После конденсора параллельный пучок лучей попадает на светоделительную пластинку 6 со светоделительным покрытием. Она делит падающий пучок пополам: один пропускает, а другой отражает.
Отраженный от пластинки 6 пучок собирается в фокусе микрообъектива 8(2) на поверхности зеркала с фазовым объектом, после отражения от которой снова проходит через микрообъектив 8(2), пластинку 6 и собирается в фокусе объектива 10, где наблюдается изображение исследуемого фазового объекта. Зеркало 11 направляет пучок лучей в визуальный тубус.
Второй пучок, пройдя через пластинку 6, компенсатор 7, собирается в фокусе микрообъектива 8(1) на эталонном зеркале 9, отразившись от которого, снова проходит через микрообъектив 8(1), компенсатор 7, падает на разделительную пластинку 6 и не участвует в образовании изображения.
Другая часть лучей отражается от пластинки 6 и интерферирует с лучами первой ветви микроинтерферометра, образуя резкое изображение интерференционных полос в бесконечности. Это изображение объективом 10 переносится в фокальную плоскость окуляра 12. Вместо окуляра в визуальный тубус вставляется ПЗС камера.
Таким образом, изображение интерференционных полос и фазового объекта получается в фокальной плоскости окуляра (ПЗС камеры), и налагаются друг на друга.
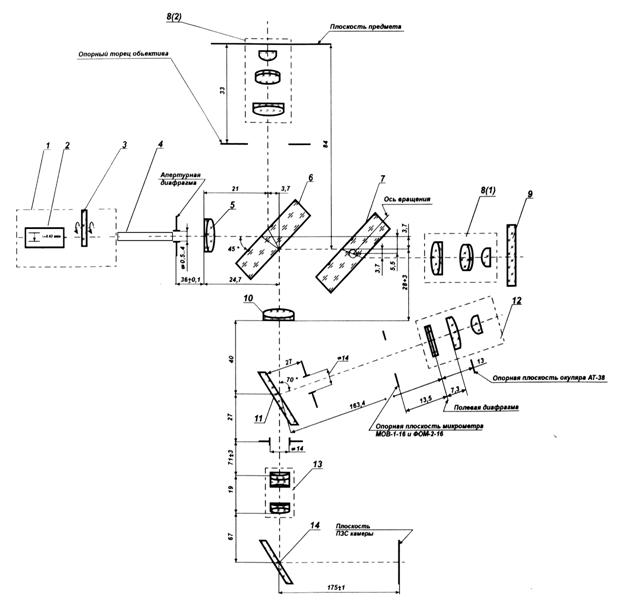
1- блок разрушителя когерентности (блока управления), 2-лазер, 3-диффузор, 4-световод, 5-конденсор, 6-разделительная пластина; 7-компенсатор 8(1), 8(2)-микрообъективы 9--эталонное зеркало;10 –проекционный объектив; 11, 14-зеркало, 12-окуляр; 13-гомаль.
Рисунок 7.32 – Оптическая схема автоматизированного микроскопа
При вынутом окуляре (ПЗС камере) в плоскости выходных зрачков микроинтерферометра наблюдаются два изображения апертурной диафрагмы, которые являются выходными зрачками системы; от их положения друг относительно друга зависит форма и положение интерференционных полос. При изменении взаимного расположения зрачков и расстоянии между ними соответственно изменяются ширина интерференционных полос и их направление. Для этой цели в микроинтерферометре предусмотрены подвижки изменяющие положение микрообъектива 8(1): при его смещении относительно оптической оси меняется угол схождения пучков, а следовательно, и ширина образуемых ими полос, при вращении смещенного микрообъектива относительно оптической оси один из зрачков будет описывать окружность относительно другого и будет меняться ориентация полос (рис. 7.32).
Микроинтерферометр имеет два канала регистрации: окулярный и фотографический. В каждом канале установлены ПЗС камеры: камера окулярного канала, камера фотографического канала. Каналы центрованы, т.е. центр изображения, получаемого в окулярном канале, совпадает с центром изображения фотографического канала.
Для регистрации изображения с помощью ПЗС камеры фотографического канала зеркало 11 выключается из хода лучей и свет, пройдя через гомал 13 и отразившись от зеркала 14, попадает на плоскость камеры (рис. 7.32).
Внешний вид АИМ представлен на рис. 7.33.

1-автоматизированный двухкоординатный предметный стол; 2-опорное зеркало на пьезоэлементе (пьезозеркало); 3-ПЗС-камера окулярного канала; 4-микроинтерферометр МИИ-4 ЛОМО; 5-ПЗС-камера фотографического канала; 6-осветительный блок с разрушителем пространственной когерентности.
Рисунок 7.33 – Автоматизированный микроскоп (внешний вид)
Программно-аппаратный комплекс (ПАК) предназначен для сопряжения прибора с ПЭВМ и выполняет следующие функции:
- выдача управляющих сигналов на плату управления пьезозеркалом;
- выдача управляющих сигналов на пьезозеркало с платы управления пьезозеркалом;
- выдача управляющих сигналов на плату управления предметным столом;
- выбор ПЗС камеры;
- оцифровки видеосигнала, поступающего с ПЗС- камер и его передача в ПЭВМ;
- восстановление трехмерного профиля по набору интерференционных изображений;
- визуализация полученных результатов.
ПАК включает в себя:
- ПЭВМ с операционной системой (Windows 2000/XP);
- плату ввода изображения;
- плату управления пьезозеркалом;
- PCI IO контроллер;
- программу захвата кадров;
- программу для реконструкции ОРХ – «WinPhast» (Сухоруков К.А. (ВНИИОФИ)).
Получаемый с ПЗС-камеры видеосигнал поступает на плату ввода изображения, где производится его оцифровка и запись в ПЭВМ. Захват кадров производится с помощью программы TVMicro-2 (Рейтблат Г., ЭНИМС). Программа запускается из основной программы «WinPhast» и позволяет управлять захватом интерференционных изображений, работой пьезозеркала и шаговыми двигателями предметного столика.
После захвата кадров производится восстановление фазового изображения по алгоритму, использующему дискретный фазовый сдвиг между интерферограммами. Программа позволяет:
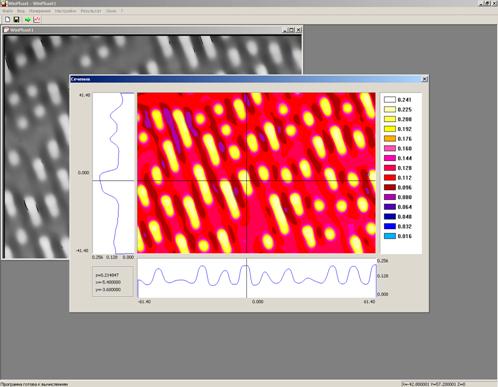
а
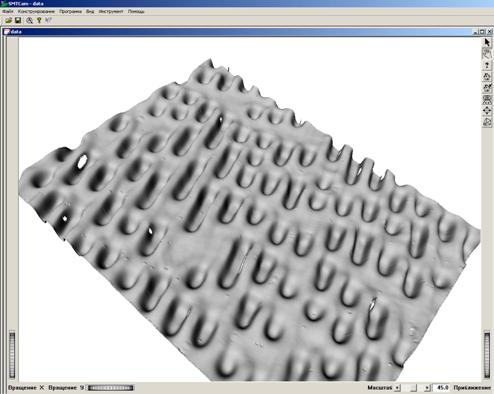
б
а- окно модуля реконструкции; б- окно модуля трехмерной визуализации. Объект исследования – поверхность компакт-диска.
Рисунок 7.34 – Программный комплекс
- восстанавливать фазовое изображение по интерференционным изображениям (рис. 7.34 а);
- разворачивать (сшивать) фазу;
- вычитать плоскость (клин);
- визуализировать результаты измерений (сечения, 3D) (рис. 7.34 б).
Лазерное излучение, имеющее высокую пространственную когерентность, при прохождении через оптическую схему микроскопа создает в его поле зрения спекл-картину. Поэтому для уменьшения влияния спекл-шума необходимо, чтобы за время регистрации в одну и ту же точку регистратора приходили волны некогерентные по пространству. Для этой цели применяют так называемые разрушители когерентности. В данном приборе был использован разрушитель когерентности на основе вращающегося диффузора. Ниже приведен расчет размера его зерна.
Диффузор, представляющий диск из светорассеющего стекла, вращается при помощи двигателя ДПМ-20-Н1-08Т. В номинальном режиме двигатель имеет угловую скорость w=75 с-1. На диффузор проецируется пятно от лазерного модуля диаметром D. Центр пятна отстоит от оси вращения диффузора на расстоянии R. Предположим, что зерна имеют вид окружностей диаметром d. Тогда (рис.7.35) минимальной линейной скоростью будут обладать те зерна, которые отстоят от центра на расстояния R+D/2.
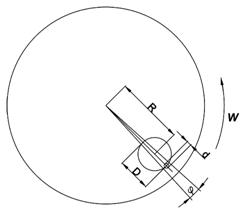
Рисунок 7.35 – Вычисление размера зерна светорассеивающего стекла.
Из геометрических соображений размер зерна будет равен:
|
|
(7.26) |
Вследствие малости угла j (7.26) можно записать как:
|
|
(7.27) |
Время регистрации одного пикселя с помощью ПЗС камеры определяется временем накопления и равно tнак=20мс. Предположим, что за это время в поле зрения окажутся N зерен, тогда время прохождения одного зерна tзер будет равно:
|
|
(7.28) |
За это время диффузор повернется на угол:
|
|
(7.29) |
Из (7.27-7.29) следует, что размер зерна равен:
|
|
(7.30) |
При R=12мм, d=1мм, w=75 с-1 и N=100 (зерен) получаем, что
|
|
(7.31) |
Таким образом, в качестве диффузора необходимо выбирать светорассеивающие стекла с размером зерна не более 190 мкм.
Для реализации метода фазовых шагов было разработано зеркало с пьезоэлементом (пьезозеркало).
В составе пьезозеркала был использован пьезоэлемент КП-1 выпускаемый фирмой «Элпа». Чертеж узла приведен на рис. 7.36. Узел имеет посадочное место позволяющее установить его вместо штатного узла опорного зеркала микроскопа МИИ-4(М). Штатное опорное зеркало микроскопа клеится на оправу 4. Регулировочный винт 12 позволяет плавно изменять положение опорного зеркала 5 и тем самым подстраивать контраст полос.
Для управления пьезоэлементом была разработана схема управления, подключаемая к LPT порту ПЭВМ.
1- корпус, 2- фланец, 3 –втулка, 4-оправа зеркала, 5- зеркало, 6- шайба, 7-винт, 8, 10 - гайка, 9- сухарь, 11 –контргайка, 12- винт регулировочный.
Рисунок 7.36 – Узел опорного зеркала автоматизированного микроскопа.
Получаемую на микроскопе интерферограмму можно записать в виде следующего уравнения (7.32):
|
|
(7.32) |
где I(x,y) - регистрируемое с помощью камеры распределение интенсивности интерференционной картины; I1(x,y) I2(x,y)-интенсивности предметного и опорного каналов; f0 – частота полос; F(x,y) –фазовый набег (ОРХ) на исследуемом объекте, являющейся искомой величиной.
Обозначим A(x,y)=I1(x,y)+I2(x,y), B(x,y)=2![]() и перепишем (7.32) в виде (7.33):
и перепишем (7.32) в виде (7.33):
|
|
(7.33) |
Для нахождения функции F(x,y) требуется решить уравнение (7.32), при этом необходимо знать остальные параметры. Другой путь – решение четырех уравнений, для различных значений фазового сдвига ![]() (N=0, 1, 2, 3)
(N=0, 1, 2, 3) ![]() , l-- длина волны излучения
, l-- длина волны излучения
|
|
(7.33) |
а параметры A(x,y), B(x,y), d и F(x,y) выступают как неизвестные. Это и есть суть метода фазовых шагов (алгоритм Carre).
Фазовый сдвиг вносится с помощью пьезозеркала, находящегося в опорном канале и управляемом от ПЭВМ. Алгоритм фазовых шагов – самокалибрующийся, величина d также является неизвестной. Важно лишь то, чтобы она была постоянной для каждого шага.
В результате имеется система из 4-х уравнений:
|
|
(7.34) |
Исключая последовательно неизвестные A(x,y), B(x,y), d, находим выражение для разности фаз:
|
|
(7.35) |
Функция арктангенс (7.35) определена в интервале [-p/2; p/2]. Знаки синуса и косинуса фазы, определяемые из уравнений (7.34) позволяют однозначно определить фазу в интервале [-p; p]. Однако, в тех случаях, когда искривление волнового фронта превышает 2π, распределение фазы определяется с точностью ![]() , где
, где ![]() и т.д. Поэтому следующим шагом в обработке результатов измерений является решение задачи восстановления истинной формы волнового фронта, которая получила название разворачивание или «сшивка» фазы.
и т.д. Поэтому следующим шагом в обработке результатов измерений является решение задачи восстановления истинной формы волнового фронта, которая получила название разворачивание или «сшивка» фазы.
Суть этой операции заключается в добавлении каждому элементу массива «несшитой фазы» значения ±2pn где n – целое число. Число n выбирается для каждого элемента таким образом, чтобы разность между значениями данного и какого-либо уже обработанного соседнего элемента была меньше n по абсолютной величине и определяется производной в соседних точках.
Ошибка в выборе n для одного из элементов, вызванная шумом в исходных данных, может распространяться на все последующие. Поэтому до сшивки необходимо выявить и отметить на специальной карте дефектные элементы, в которых Dj вычислено с большой погрешностью. Эти элементы должны быть обойдены при сшивке.
Используется два различных подхода к обнаружению дефектных элементов. Во-первых, фаза Dj вычисляется с большой погрешностью в точках, где величина В(x,y) (формула 7.33) сравнима с уровнем шума (величина В(x,y) зависит от коэффициента зеркального отражения объекта). При втором подходе проводится локальная сшивка фазы в окрестности каждого элемента массива, а затем численно определяются вторые производные «сшитой фазы» по координатам. Если хотя бы одна из них превышает задаваемый порог, элемент считается дефектным. Как правило, такие элементы появляются в точках, где величина погрешности значительно превышает средний уровень шумов.
После того, как получена карта «плохих» точек, используется алгоритм сшивки фазы в произвольной связной области. В качестве побочного результата этот алгоритм дает карту сшитых элементов. Значения остальных элементов на распределении результата вычислений считаются неопределенными. Если область недефектных элементов несвязная, сшивка будет проведена только для одной из ее связных частей. Чтобы выбрать нужную из них, координаты начала сшивки задаются отдельно.
Для уменьшения шума в распределении фазы исходные интерферограммы могут усредняться, а также пропускаться через линейный или медианный сглаживающий фильтры.
Для устранения наклона, связанного с наблюдением в полосах конечной ширины, из распределения сшитой фазы вычитается линейная функция от переменных х,у, коэффициенты в которой подбираются по методу наименьших квадратов.
Точность реконструкции в условии ограниченного угла зондирования зависит от траектории сбора проекционных данных. Она максимальна, когда траектория сканирования двумерна (2D), а получающиеся проекции равномерно распределены по сетке углов. Для реализации такой схемы зондирования было предложено смещать точечный источник в плоскости апертурной диафрагмы интерференционного микроскопа Линника (рис. 7.21,в). Как известно изображение объекта в этом микроскопе формируется в отраженном свете, так как объект расположен на зеркальной поверхности, и излучение дважды проходит через него. Это обуславливает особенности томографической схемы получения проекций, т.н. «зеркальной» схемы.
Рассмотрим задачу «зеркальной» томографии, т.е. томографии фазовых объектов, расположенных вблизи зеркальной поверхности произвольной формы, с частным случаем томографии фазовых объектов у плоского зеркала.
Схема зондирования объекта представлена на рис.7.26. На нем видно, что зондирующая плоская волна от любого точечного источника дважды проходит через объект под одним и тем же углом относительно оптической оси z. На рис.7.37 приведена эквивалентная схема зондирования. В этой схеме объект дополняется своим зеркальным отражением.

Рисунок 7.37 – Эквивалентная схема зондирования объекта.
Пусть функция ![]() описывает трехмерный (3D) фазовый объект, который можно заключить в шар радиуса
описывает трехмерный (3D) фазовый объект, который можно заключить в шар радиуса ![]() . Эта функция связана с 3D пространственным распределением показателя преломления
. Эта функция связана с 3D пространственным распределением показателя преломления ![]() следующим соотношением:
следующим соотношением:
|
|
(7.36) |
где n0 – показатель преломления окружающей объект среды, l - средняя длина волны квазимонохроматического излучения. Предполагается, что начало координат помещено в центр объекта (шара радиуса ![]() ).
).
Для записи функции объекта с его зеркальным двойником ![]() сместим начало координат вдоль оси z на величину
сместим начало координат вдоль оси z на величину ![]() в точку 0 на зеркале 7 (см. рис.2а). Тогда такой составной объект описывается функцией
в точку 0 на зеркале 7 (см. рис.2а). Тогда такой составной объект описывается функцией
|
|
(7.37) |
Из приведенных рассуждений следует, что «зеркальная» томография исходного объекта (7.36) сводится к обычной томографии составного объекта (7.37). Особенности заключаются в том, что функция (7.37) - четная по координате z и область ее задания представляет собой два соприкасающихся шара.
Так как выходная плоскость 12 (рис.7.25) параллельна плоскости (x,y), то это означает, что мы имеем планарную схему регистрации двумерных (2D) параллельных проекций. В этом случае уравнение 2D проекции объекта (7.37) запишется в виде:
|
|
(7.38) |
где (q, j) – полярный и азимутальный углы единичного вектора зондирования. Еще одна отличительная особенность «зеркальной» томографии заключается в том, что проекции для углов (q, j) и (q, j+p) идентичны. Этот факт следует из свойства взаимной обратимости лучей в оптике. Действительно, из рис.7.26 видно, что при перестановке местами падающего и отраженного от зеркала пучков, вид проекции не изменится. Отсюда следует, что угол зондирования j можно ограничить диапазоном [0, p).
В микроскопе Линника формируется изображение (7.26), представляющее собой сумму элементарных интерферограмм (7.25).
Конфокальная оптическая система формирует в пространстве изображений 3D суммарное изображение из набора параллельных пучков света, несущих информацию о проекциях. В нашем случае эти пучки несут информацию не о самой проекции, а ее интерферограмме. Поэтому можно сказать, что распределение интенсивности света в пространстве изображений микроскопа Линника описывается суммарным изображением из интерферограмм-проекций фазового объекта.
Из (7.22), (7.23) следует, что даже в области локализации интерференционных полос (плоскость 12, рис.7.25) они имеют не единичный контраст, т.к. в (7.23) суммируются интерферограммы разных проекций. Поэтому для увеличения контраста желательно уменьшать угловой размер источника света. Но при этом могут появиться когерентные шумы в изображении интерферограммы.
При формировании суммарной интерферограммы (7.23) от протяженного источника происходит усреднение случайных шумов в изображениях отдельных элементарных интерферограмм. Это связано с тем, что они образованы с помощью пучков света, прошедших через различные участки оптических элементов микроскопа. В результате это приводит к уменьшению шумовой составляющей в проекциях. При дальнейшем увеличении размера источника будет, во-первых, уменьшаться контраст интерференционных полос и, во-вторых, изменится характер проекционных данных. Только для бесконечно малого точечного источника на выходе микроскопа создается интерферограмма идеальной (радоновской) проекции (7.38). Для источника малых, но конечных размеров проекционные данные представляют собой сумму интерферограмм проекций из небольшого диапазона углов зондирования и лишь в некотором приближении их можно принять за проекцию. Аналогичная ситуация возникает в любой оптической системе регистрации проекционных данных, имеющей конечную числовую апертуру.
Таким образом, при выборе размера источника необходимо поддерживать разумный компромисс между качеством изображения интерферограммы и достоверностью описания проекционных данных с помощью уравнения проекции (7.38).
Для сбора проекций использовался автоматизированный интерференционный микроскоп Линника. Наклонное освещение объекта достигалось за счет смещения источника освещения. Для автоматической расшифровки интерферограмм использовался программный комплекс «Phast» (ВНИИОФИ, Шумский Е.) реализующий метод 4-х фазовых шагов.
В качестве фазового объекта была выбрана живая клетка крови - лимфоцит. Клетки находились в физиологическом растворе, показатель преломления которого 1.334, между тонким покровным стеклом и плоским зеркалом. Этот раствор выполнял также роль иммерсионной жидкости для фазового объекта. Для зондирования была выбрана двумерная дискретная траектория «квадрат». В этом случае геометрическое место точек с угловыми координатами вектора зондирования на плоскости (q,j) совпадает с узлами прямоугольной сетки. Шаг сетки по j составил 30° в диапазоне 0°-150°. Диапазон изменения угла зондирования по углу q для 100-кратного иммерсионного микрообъектива с NA=1.25 составил 90°. Точность установки угловых значений – 0.5 град. Всего было зарегистрировано 43 двумерные проекции на сетке 256´256, размер кадра 23´23 мкм. Проекции приведены на рис. 7.38.
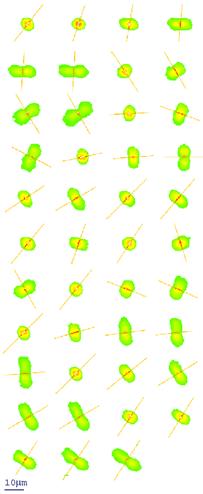
Рисунок 7.38 - Набор экспериментальных проекций лимфоцита.
После автоматической расшифровки интерференционных картин получается система уравнений вида
|
|
(7.39) |
где ![]() - ОРХ, накопленная на пути по i-му лучу; Bi, Ci - точки его входа и выхода в исследуемую область; n(s) - показатель преломления исследуемого объекта вдоль этого луча; n0 - показатель преломления окружающей среды, предполагаемый постоянным; l - длина волны.
- ОРХ, накопленная на пути по i-му лучу; Bi, Ci - точки его входа и выхода в исследуемую область; n(s) - показатель преломления исследуемого объекта вдоль этого луча; n0 - показатель преломления окружающей среды, предполагаемый постоянным; l - длина волны.
Таким образом, с помощью автоматизированного интерференционного микроскопа Линника был получен набор двумерных параллельных проекцией, имеющих полярный угол q и азимутальный угол j, определяющими направляющий вектор семейства отрезков.
На этапе предварительной обработки проекций решалось несколько задач. Первой проблемой было согласование систем координат, в которых определены проекции, и системы координат, относительно которой реконструируется клетка. Такое согласование было осуществлено при помощи соотношения, связывающего первый момент трехмерного объекта с первыми моментами его двумерных проекций. По этому соотношению, центр масс (u0, v0) двумерной проекции f(u, v) совпадает с проекцией на плоскость детектирования центра масс (x0, y0, z0) самого трехмерного объекта g(x, y, z). Таким образом, согласованные системы координат получаются при помещении начала координат для каждой проекции в ее центр масс.
К процедурам согласования можно отнести также и «энергетическую» нормировку проекций. В рассматриваемой модели сбора данных нулевые моменты («энергии») всех проекций должны быть равны между собой. Однако данные поступали с разных каналов, поэтому были возможны ошибки, связанные с разбросом чувствительности каналов и погрешностями их калибровки. Устранение такого рода ошибок можно производить путем мультипликативной нормировки проекций, при которой их нулевые моменты приводятся либо к среднему, либо к заданному значению.
Помимо упомянутого согласования, на этапе предобработки производилось и устранение фона. Из проекций вычиталась некоторая константа (вообще говоря, для каждой - своя), которая оценивалась приближенно по значениям вне изображения клетки. Получившиеся при этом отрицательные числа заменялись нулем. Также приравнивались нулю значения проекции в точках, лежащих вне круга определенного радиуса.
Для проекций, снятых в установке с зеркалом, дополнительно производилась проверка на совпадение измеренных углов q и j с этими же углами, вычисленными по критерию максимальности суммы квадратов линейных интегралов в направлении, перпендикулярном линии зеркала. В численном моделировании было показано, что полученное рассогласование в несколько градусов не должно привести к заметным ошибкам реконструкции. Поэтому для расчётов брались те значения углов, которые были измерены.
Для восстановления томограмм использовался комбинированный итерационный алгоритм cART. Зеркало располагалось в плоскости Z=0. После каждой итерации отрицательные значения восстановленной функции заменялись на нулевые. За ноль принимались также значения полученной функции вне области задания объекта в виде двух шаров радиуса 0.5, расположенных симметрично относительно зеркала (плоскости Z=0). Центры шаров расположены на оси Z, на расстоянии 0.5 от зеркала. Расстояния даны в безразмерных единицах, в которых область реконструкции - куб с длиной стороны 2. Нормированная невязка с проекционными данными - 37.3%. На рис.4.3 приведена 3D реконструкция внутренней структуры лимфоцита в виде изображения трех изоповерхностей оптической плотности 22%, 50%, 82% от максимального значения. Реконструкция томограммы выполнена Пикаловым В.В.
Таким образом, к основным достоинствам томографического микроскопа по схеме Линника относятся:
- высокая чувствительность измерения ОРХ из-за двойного прохода излучения через объект;
- реализация схемы со сканированием пучка относительно неподвижного объекта;
- угол зондирования - ±45°;
- траектория зондирования – «квадрат», обеспечивающая минимальную ошибку реконструкции.
Однако, основной недостаток схемы связан со сложностью реконструкции по «зеркальным» проекциям. Для решения этой проблемы необходимо использовать схему с однократным прохождением излучения сквозь объект.

Рисунок 4.39 - 3D томограммы лимфоцита (пояснения в тексте). Реконструкция выполнена Пикаловым В.В..
Для преодоления сложностей реконструкции по зеркальным проекциям в работе было предложено использовать проекции, полученные при однократном прохождении излучения сквозь объект. В основе схемы такого микротомографа лежит конфокальный микроскоп.
Обычно считается, что применение точечной диафрагмы в конфокальном сканирующем микроскопе позволяет достичь избирательную селективность по глубине объекта. При этом не принимается во внимание тот факт, что получаемые данные представляют собой луч-суммы по прямым, проходящим через вершину конуса или веера (область зондирования отмечена серым на рис.7.18). Наиболее адекватный подход к решению этой проблемы связан с применением принципов томографии. Для этого необходимо разработать алгоритм для получения проекций в параллельных пучках (и в дальнейшем использовать классические методы восстановления по набору проекций в параллельных пучках) из проекций в конусном пучке. Рассмотрим это более подробно.
При зондировании объекта конусным (в двумерном случае – веерным пучком), что по существу и происходит в конфокальном сканирующем микроскопе (см. рис. 7.18), возможны два варианта зондирования: перетяжка пучка находится внутри объекта (обычная схема, используемая в конфокальном микроскопе) (рис. 7.40, а) и перетяжка находится вне объекта (рис. 7.40, б). При этом сканирование объекта, происходит в плоскости, перпендикулярной оси конуса.
Рассмотрим более подробно двумерный случай при схеме зондирования, представленной на рис. 7.40, б. Вариант схемы, когда объект находится выше области перетяжки, не используется, так как изображение будет мнимым.
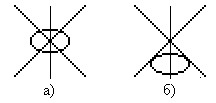
а) в конфокальном микроскопе б) в конфокальном томографическом микроскопе
Рисунок 7.40 – Схемы зондирования объекта конусным пучком
Для простоты, предположим, что движение совершает не объект, а источник зондирующего излучения вместе с регистратором (рис. 7.41). В сканирующем конфокальном микроскопе источник и регистратор неподвижны, а движется сам объект, расположенный на сканирующем столике, т.е. реализуется схема scanning stage.

Рисунок 7.41 – Формирование параллельных проекций в конфокальном томографическом микроскопе.
Будем рассматривать веерный пучок как набор лучей исходящих из одной точки под определенным углом. Он представляет сечение плоскостью конусного пучка, проходящее через вершину конуса. Каждый луч в веерном пучке зондирует объект под своим углом. Крайние лучи веера зондируют объект под большими углами, а центральные – под малыми.
В одномерном случае источник и регистратор движутся по прямой относительно неподвижного объекта, а на регистраторе формируется набор веерных планарных проекций. При зондировании объекта веерным пучком всегда можно выделить те лучи, которые зондируют объект под одним и тем же углом. Выделив из всех веерных проекций наборы таких лучей, мы получим проекции в параллельных пучках (рис.7.41). В этом заключается смысл алгоритма. Каждый луч в веерном пучке попадает на свой фотоэлемент матрицы (пиксел). Так как луч в веерном пучке распространяется под своим углом, то количество углов зондирования определяется числом пикселов на фотоприемнике. Следовательно, общее число проекций зависит от количества пикселов на матрице. А вот количество отсчетов в каждой проекции будет зависеть от количества шагов сканирования.
Таким образом, каждому пикселу (отсчету) соответствует определенный угол зондирования (рис. 7.42).
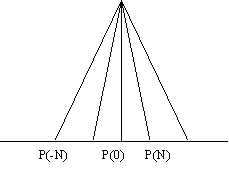 |
Рисунок 7.42– Связь угла зондирования и отсчета проекции
Пусть нумерация отсчетов в проекции будет вестись относительно центра проекции т.е. –N,..., 0,…, N, где –N и N – крайние точки, а 0 – центральная точка, общее количество отсчетов - 2N. Каждому отсчету будет соответствовать свой зондирующий угол: ![]() (
(![]() ). Выделим в плоскости объекта сечение с наибольшей протяженностью вдоль направления зондирования, веер лучей при движении вдоль этого направления осуществляет зондирование всего объекта. Для получения всей информации об объекте необходимо, чтобы в крайних положениях крайние точки освещались под максимальными углами.
). Выделим в плоскости объекта сечение с наибольшей протяженностью вдоль направления зондирования, веер лучей при движении вдоль этого направления осуществляет зондирование всего объекта. Для получения всей информации об объекте необходимо, чтобы в крайних положениях крайние точки освещались под максимальными углами.
В результате сканирования получаются одномерные матрицы изображений 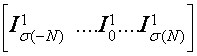 …
… ![]() …
… ![]() , где I – интенсивность пикселя, верхний индекс – шаг перемещения источника (1 - M) при его дискретном движении, нижний индекс – угол соответствующий данному пикселю. Из набора таких проекций выбираем те, которые имеют одинаковый нижний индекс (угол зондирования) и формируем из них новые проекции, которые будут являться проекциями объекта в параллельных пучках:
, где I – интенсивность пикселя, верхний индекс – шаг перемещения источника (1 - M) при его дискретном движении, нижний индекс – угол соответствующий данному пикселю. Из набора таких проекций выбираем те, которые имеют одинаковый нижний индекс (угол зондирования) и формируем из них новые проекции, которые будут являться проекциями объекта в параллельных пучках:
![]() …
…![]() …
… ![]() .
.
Т.о. число проекций равно числу отсчетов в изображении (2N+1), а число отсчетов в проекции равно числу шагов сканирования (M).
В силу симметрии аналогичные рассуждения имеют место при синтезе двумерных параллельных проекций из конусных (рис. 7.43).

Рисунок 7.43 – Получение двумерных параллельных проекций по набору двумерных конусных проекций (m- число шагов сканирования, n- число проекций).
Например, если требуется получить 30 проекций размерностью 64x64 пиксела, то число шагов сканирования равно 4096, а число выделяемых углов зондирования (пикселей на изображении) равно 30.
Такая система сбора проекционных данных может быть легко реализована в конфокальном микроскопе, для этого необходимо, чтобы перетяжка пучка находилась выше объекта. Для получения конусных проекций необходимо лишь обеспечить двумерное плоско-параллельное сканирование объекта и заменить точечный фотоприемник – матрицей фотоэлементов. Как правило, для томографической реконструкции используется не более 100 проекций. Тогда число элементов фотоприемника должно быть равно 100 (матрица 10×10). Такое небольшое число элементов позволяет использовать фотоприемники, составленные из различных дискретных фотоэлементов (например, ФЭУ).
Плоско-параллельное сканирование в зоне конусного пучка представляет еще один способ сбора проекционных данных в схемах со сканированием объекта относительно неподвижного пучка. Его основные преимущества по сравнению со схемами, использующими вращение или наклон, заключаются в том, что:
- объект не выходит из фокуса во время сканирования, т.е. нет необходимости в создании сложных механизмов и алгоритмов, обеспечивающих выравнивание объекта относительно оси вращения;
- его легко можно реализовать в микроскопе, поместив объект на предметный сканирующий столик.
В данной схеме траектория сбора данных определяется геометрией расположения элементов фотоприемника, т.е. можно обеспечить любую траекторию, в том числе и «квадрат», использовав матрицу фотоприемников.
Однако для достижения максимального угла зондирования необходимо применение микрообъективов с большой числовой апертурой (иммерсионных) и большим рабочим отрезком.
На рис. 7.44 представлена оптическая схема конфокального томографического интерференционного микроскопа. Схема реализует интерферометр Маха-Цендера с автоматизированной расшифровкой интерферограмм по методу фазовых шагов. Излучения – Hе-Ne – лазер 1, проходит через расширитель с пространственным фильтром 2,3,4 и попадает на светоделитель 5 и делится по амплитуде пополам. Одна часть излучения формирует опорный пучок, другая предметный. В предметном канале микроскопа реализована оптическая схема конфокального микроскопа. Но, в отличие от классической схемы, перетяжка пучка находится вне объекта, а на фотоприемнике 14 строится его изображение (рис. 7.45). Сам объект располагается между двумя покровными стеклами, которые в свою очередь расположены между двумя идентичными иммерсионными объективами 8,9 с большой числовой апертурой NA=1.3, ×100. Прохождение излучение через такую систему показано на рис. 4.46. Угол зондирования равен:
|
|
(7.40) |
где nср – показатель преломления среды, в которой находится объект. Для nср=1.33 (физ. раствор) и NA=1.3 угол s3=78° (2s3=156°). Реальные эксперименты показали, что достигается угол 2s3=100°.
Таким образом, после реконструкции ОРХ формируется набор конусных проекций.

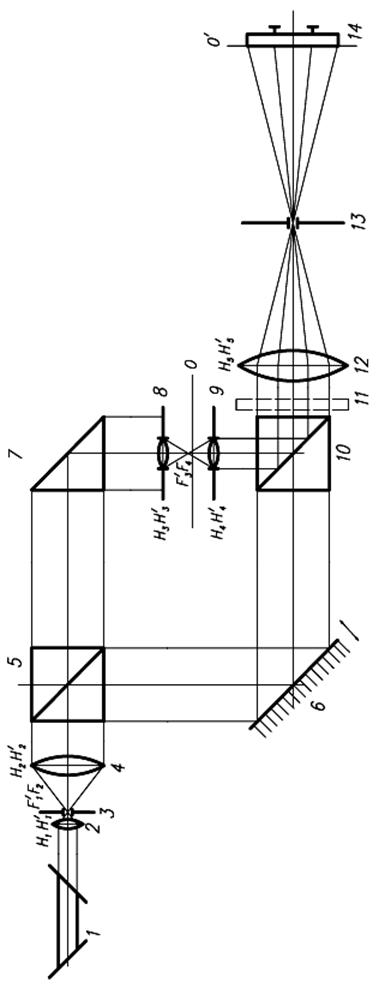


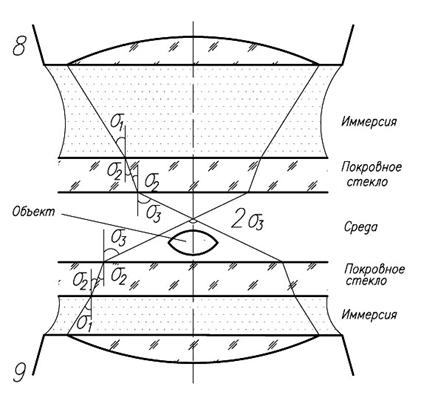
Рисунок 7.46 – Схема зондирования объекта. 8,9 - иммерсионные микрообъективы.
Из полученного набора конусных проекций по выше приведенному алгоритму формируются параллельные проекции. Далее с помощью пакета программ предобработки «PRETOM» (Шумский Е., ВНИИОФИ) производилась подготовка проекционных данных, включающая в себя:
- медианную фильтрацию проекций;
- растяжение проекции в зависимости от угла;
- энергетическую нормировку;
- сдвиг проекций в центр тяжести.
Томограмма реконструировалась с помощью пакета программ «TOMО» (Шумский Е., ВНИИОФИ) итерационным алгоритмом Гершберга - Папулиса.
На рис. 7.47 приведены проекции и томограммы традесканции

а
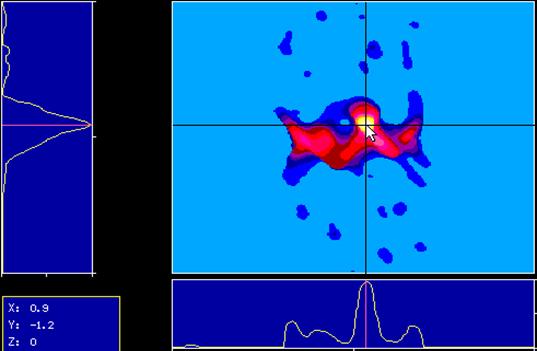
б
а – экспериментальные проекции традесканции; б- томограмма, реконструированная по алгоритму Гершберга-Популиса в программе «TOMО» (Шумский Е., ВНИИОФИ)
Рисунок 7.47
Таким образом, конфокальный томографический интерференционный микроскоп обеспечивает схему с движением объекта относительно неподвижного пучка, при этом получение проекционных данных обеспечивается за счет плоско-параллельного движения в коническом пучке и достигается угол зондирования ±50°.
Однако данная схема требует применения иммерсионных объективов с большим рабочим отрезком. Для объективов с большим увеличением и, соответственно, малым рабочим отрезком необходимо было разработать другую схему микротомографа. Одновременно была поставлена задача дальнейшего увеличения угла зондирования. Решение было найдено в использовании специального иммерсионного конденсора.
Одной из главных задач микротомографии является увеличение угла зондирования. Рассмотренные выше схемы зондирования предполагают различные способы увеличения зондирующего угла. Однако, максимальный угол зондирования не превысил ±50° градусов.
Возможным решением проблемы увеличения угла зондирования является применение иммерсионных объективов, имеющих большую числовую апертуру (NA). В таблице 7.3 представлены основные микрообъективы и соответствующие им максимальные углы зондирования для среды n=1.33 вычисленные по формуле (7.40)
Таблица 7.3
| Типы объективов |
Увеличение, крат |
Числовая апертура (NA) |
Угол зондирования 2s3, град |
| Сухие |
10 20 40 60 |
0.25 0.40 0.65 0.85 |
21.6 35 58.5 79 |
| Иммерсионные |
90 100 |
1.2 1.3 |
129 156 |
Как видно из таблицы и формулы (7.40), максимальный угол зондирования определяется числовой апертурой объектива. Для NA=1.3 и n=1.33 (физ. раствор), угол достигает 78º.
Для увеличения угла зондирования объекта в настоящей работе предложено использовать иммерсионный конденсор. При использовании иммерсионного объектива с числовой апертурой NA, угол зондирования a2 (рис. 7.48) для объекта, находящегося в среде с показателем преломления n2 будет равен:
|
|
(7.41) |
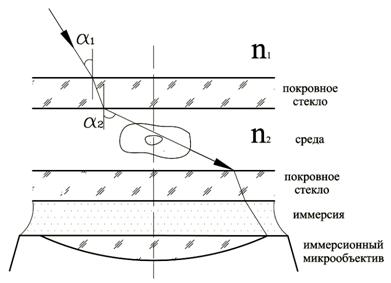
Рисунок 7.48 – Схема зондирования объекта.
В микроскопе излучение источника проходит по воздуху (n1=1) и попадает в среду (n2>1). Основным является вопрос о том, как обеспечить такой угол зондирования в среде n2. Для этого излучение должно проходить через среду n1 с показателем преломления большим 1. Действительно, с учетом выражения (7.41) для n1 справедливо соотношение (7.42)
|
|
(7.42) |
так как sin(a1) лежит в диапазоне 0…1, то n1≥NA.
Таким образом, при использовании микрообъектива с числовой апертурой NA>1, максимальный угол зондирования объекта, находящегося в среде с показателем преломления nср, равен 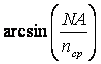 , при условии распространения излучения в конденсоре со средой, показатель преломления которой больше, чем NA.
, при условии распространения излучения в конденсоре со средой, показатель преломления которой больше, чем NA.
Для формирования лучей зондирующего излучения, были использованы плоские зеркала, помещенные в иммерсионную среду n2 (рис. 7.49). Рассмотрим прохождение луча через такую систему. Излучение проходит по воздуху n1=1, падает перпендикулярно границе раздела n1/n2 и без преломления заходит в среду n2 (a1=a2=90º). Луч падает на плоское зеркало под углом 90-g и отражается от него под тем же углом. Исходя из соотношений:
|
|
(7.43) |
находим угол наклона зеркала:
|
|
(7.44) |
Для среды n2=1.46 (глицерин) при числовой апертуре NA=1.3 из (7.44) получаем
|
|
(7.45) |
![]()

Рисунок 7.49 – Углы преломления луча при прохождении через среды конденсора.
Была разработана конструкция зеркального иммерсионного конденсора (рис. 7.50).
Конденсор представляет собой оптическое устройство, позволяющее освещать исследуемый объект наклонными плоскими пучками под разными ракурсами. Угол зондирования определяется наклоном зеркал и одинаков для всех ракурсов. Количество ракурсов равно числу зеркал. В изготовленном экспериментальном экземпляре конденсора число зеркал (ракурсов) равно 10 (рис. 7.50). На рис. 7.51 представлена фотография этого устройства.

1- плоское зеркало; 2,4- защитные стекла; 3- иммерсия; 5- корпус.
Рисунок 4.50 – Конструкция зеркального иммерсионного конденсора

Рисунок 7.51 – Внешний вид зеркального иммерсионного конденсора
Для того чтобы обеспечить числовую апертуру больше 1 в конденсор заливается иммерсионная жидкость с соответствующим показателем преломления. Используя жидкости с различными показателями преломления, можно менять числовую апертуру и соответственно угол зондирования. Угол наклона зеркал был рассчитан для NA=1.3 и n=1.46 (см. (7.45)) и равен 58º (рис. 7.49).
Так как этот угол жестко определен конструкцией конденсора и задает угол a3, то при увеличении показателя преломления n2 (при смене иммерсии), возможен эффект полного внутреннего отражения. Критическое значение n2 составит:
|
|
(7.46) |
Т.е. для данной схемы (для заданного угла b) показатель преломления иммерсии должен быть n2< n2кр=1.49. Можно выразить это ограничение и через числовую апертуру NAmax
|
|
(7.47) |
т.е. такую максимальную числовую апертуру, которая может быть реализована на данной схеме. Это важно знать для согласования с числовой апертурой объектива NAоб, которая должна быть больше NAконд конденсора, иначе параллельный пучок излучения не войдет в микрообъектив.
Таким образом, согласование числовой апертуры конденсора и микрообъектива и выбор параметров оптической схемы конденсора должно производиться в следующем порядке:
1) Выбор NAконд из условия NAконд< NAоб.
2) Исходя из показателя преломления n3 (среда, в которой находится исследуемый объект), находится угол a3.
3) Выбирается показатель преломления n2 из условия NA≤n2≤n2кр см. (7.42) и (7.47).
4) Определяется угол наклона зеркал b (7.44).
Схема зондирования объекта с использованием иммерсионного конденсора представлена на рис. 4.16. Объект зондируется плоским параллельным пучком, направляющий вектор которого имеет полярный угол q и азимутальный угол f. Число проекций определяется числом зеркал и равно 10. Зеркала расположены под одинаковыми углами в диапазоне 0-360º, равными f=36º. Полярный угол q одинаков для всех ракурсов и определяется показателем преломления промежуточной среды и среды, в которой находится объект, с учетом (7.46), по следующей формуле:
|
|
(7.48) |
где b- угол наклона зеркал, n2, n3- показатели преломления промежуточной среды и среды, в которой находится объект.
Для n2=1.46 (глицерин), n3 =1.33 (физ. раствор), b=58.5º q=78º.
Для n2=1.33 (дистиллированная вода), n3 =1.33 (физ. раствор), b=58.5º (4.5) q= 63º.

Рисунок 7.52 – Схема зондирования объекта
Была разработана и экспериментально проверена оптическая схема интерференционного томографического микроскопа (рис. 7.54), в которую был включен разработанный конденсор.
Принцип получения интерференционной картины базируется на схеме дифракции на точке (PDI – point diffraction interferometer) – опорный пучок формируется путем дифракции на малом отверстии. Данная схема отличается от классической схемы такого микроскопа (схема Полякова). Отличие в том, что для разделения исходного пучка используется не дифракционная решетка, а светоделитель.
Рассмотрим состав макета оптической схемы и проследим за ходом излучения через нее. В качестве источника излучения был использован He-Ne лазер ЛГН-215, 50мВт, l=632.8 нм. Лазер имеет значительную временную и пространственную когерентность, что важно, так как предметный и опорный пучки проходят разные пути, а разделение пучков на конденсоре происходит по фронту. Излучение лазера 1 проходит через коллиматор 2, 4 с пространственным фильтром 3, состоящего из двух объективов – микрообъектива 20х и объектива Гелиос-44, и расширяется до размера 15 мм. Разведенный пучок поступает на сканирующее устройство 6, которое состоит из призмы K-0 (кубик) с соотношением отражение/пропускание 50%/50% и поворотной призмы АР-90. Часть излучения проходит вдоль оптической оси, а другая часть, отразившись от внутренней грани кубика и пройдя через поворотную призму, формирует дополнительный параллельный пучок (боковой пучок), смещенный в поперечном направлении относительно оптической оси на расстояние D, равное расстоянию между зеркалами конденсора и оптической осью. Кубик и призма закреплены на поворотном устройстве, позволяющем вращать их перпендикулярно оптической оси рис. 7.54. При вращении сканирующего устройства, боковой пучок «пробегает» по всем зеркалам конденсора 7 (рис. 7.50).
Оба сформированных параллельных пучка проходят через исследуемый объект О. В дальнейшем, будем называть пучок, распространяющийся вдоль оптической оси – опорным пучком, а боковой – предметным пучком. Далее пучки проходят через микрообъектив 8 (Carl Zeiss, NA=1.3, b=100х). Фокальная плоскость объектива F является плоскостью фокусировки параллельных пучков. За ней формируется промежуточное изображение О’. Формирование опорного пучка происходит путем его дифракции на точечном отверстии. Для этого с помощью объектива 9 (Индустар-50) плоскость F переотображается в плоскость F’ с поперечным увеличением b=18 и расстояние между фокусами предметного и опорного пучков равно 5мм. В этой плоскости находится маска 10. Она представляет собой тонкую плоскопараллельную стеклянную пластинку, на которой наклеена круглая диафрагма с точечным отверстием. Диаметр диафрагмы 5 мм, диаметр отверстия 5 мкм. При прохождении излучения через маску диафрагмируется только центральный пучок, все боковые пучки проходят без изменения.
Плоскость промежуточного изображения О’ переотображается в плоскость O”, где наблюдается сфокусированное изображение объекта и интерференционная картина в полосах конечной ширины.
На рис. 7.53 приведено интерференционное изображение объекта.

Рисунок 7.53 – Интерферограмма эритроцита


Основными характеристиками интерференционной картины (проекции), получаемой на микроскопе, являются следующие параметры:
- ширина полос (B);
- угол наклона полос (s).
Рассмотрим подробнее эти характеристики.
Ширина полос B определяется длиной волны, углом между предметным и опорным пучками q (рис. 7.52) и расстоянием до регистратора (рис. 7.58) по следующей формуле]:
|
|
(7.49) |
где L- расстояние до регистратора, l- длина волны, D- расстояние между изображениями источников в плоскости F’. Для экспериментального макета ширина полосы составила В=45 мкм при значениях L=360мм, D=5мм, l=0.632×10-3мм.
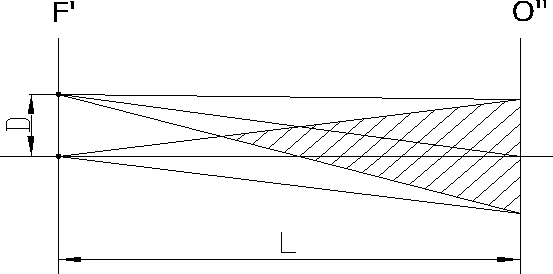
Рисунок 7.55 – Схема интерференции центрального и бокового пучков.
Из (7.49) видно, что возможным способом изменения ширины полос является изменение расстояния L, расстояния между изображениями источников D или длины волны l.
Минимальное значение B зависит от разрешающей способности регистратора (ПЗС-матрицы) и при дискретной матрице не должно быть менее 6-ти пикселей.
Максимальное значение B определяется с одной стороны алгоритмом восстановления ОРХ . С другой стороны, если увеличивать число полос путем уменьшения расстояния L, то будет возрастать коэффициент увеличения оптической схемы, что наложит ограничения на размер объектов, а также изменится (уменьшится) освещенность в плоскости регистратора.
В качестве объектов были выбраны эритроциты крови человека и лягушки. Последние имеют более сложную внутреннюю структуру, в частности, они имеют ядро.
Ориентация полос si определяется углом наклона интерферирующих пучков в плоскости регистратора и изменяется от одного ракурса к другому в зависимости от угла ориентации зеркал конденсора ji (рис.7.56)
|
|
(7.50) |
Если исключить из оптической схемы сканирующее устройство и с помощью коллиматора сформировать и направить широкий пучок на конденсор, то в плоскости регистратора будет наблюдаться интерференционная картина от всех боковых пучков с центральным опорным (рис. 7.57,а). О наличии соответствующих порядков интерференции и их ориентации можно судить после 2D фурье-преобразования изображения (рис. 7.57 б). На рис. 7.57,б отчетливо видны 10 порядков от каждого ракурса равномерно распределенные в диапазоне 0-360º и ряд других более высоких порядков.

Рисунок 7.56 – Угол наклона полос в плоскости регистратора si.

а

б
а). Интерференционная картина в плоскости регистратора при использовании широкого пучка и ее 2D Фурье-преобразование б).
Рисунок 7.57
Для реконструкции ОРХ в интерференционном томографическом микроскопе можно использовать алгоритм фазовых шагов и алгоритм с фурье-преобразованием. Для реализации алгоритма фазовых шагов требуется доработка оптической схемы: поворотную призму сканирующего устройства надо заменить на зеркало с пьезоэлементом. В данной работе рассматривался второй вариант – использование 2D фурье-преобразования. Выбор алгоритма с фурье-преобразованием обусловлен следующими особенностями:
- для восстановления требуется одно интерференционное изображение;
- отсутствие необходимости использования пьезоэлемента и его юстировки, калибровки;
- удобство использования данного алгоритма из-за большого числа полос в поле зрения, обусловленного особенностями оптической схемы микроскопа.
Для работы данного алгоритма, во-первых, необходимо обеспечить наличие базовой плоскости. Во-вторых, для градиентного алгоритма сшивки необходимо, чтобы интерферограммы не содержали разрывов полос и имели хорошую видность.
Для получения интерферограмм базовой плоскости можно использовать два метода:
- сдвигать объект так, чтобы в плоскости регистрации его было не видно. При этом необходимо, чтобы изображения соседних объектов не попадали в это поле, т.е. обеспечить минимальную плотность объектов в поле зрения. Эту операцию необходимо производить для каждого ракурса.
- использовать базовую плоскость, синтезированную цифровым способом.
Первый способ является предпочтительным, так как все аберрации, вносимые оптической системой, будут вычитаться. Но сдвиг объекта может привести к изменению положения объекта, клетка может оторваться от предметного стекла, что нежелательно. Это приведет к искажению реконструируемой томограммы, так как объект должен быть неподвижен в ходе эксперимента. Можно также заранее получить интерферограммы базы (без объекта), но при этом необходимо, чтобы положение конденсора не изменялось. В настоящей оптической схеме это сделать сложно из-за особенностей конструкции конденсора.
Поэтому базовая плоскость синтезировалась цифровым способом. Для этого применялась процедура пороговой фильтрации спектра (7.51):
|
|
(7.51) |
где L – пороговый уровень (комплексное число).

а

б
а) Интерференционная проекция б) Базовая плоскость.
Рисунок 7.58
На интерференционной проекции рис. 7.58,а кроме шумов видны зоны дефектов 2-х типов:
- с локальным уменьшение видности полос (рис. 7.59,а);
- с разрывом полосы (потерей полосы) (рис. 7.59,б).
Оба дефекта приводят к значительным искажениям восстанавливаемого фазового изображения.
|
|
|
| а |
б |
а) локальное уменьшение видности полос; б) потеря полосы.
Рисунок 7.59 - Дефекты интерферограмм
Для улучшения качества интерференционных проекций был разработан двухэтапный метод, который заключается в спектральной обработке исходной интерферограммы.
Информация об объекте заключена в искривлении полос. Присутствующие на интерферограмме дефекты и шумы имеют равномерный спектр. Поэтому для удаления шумов была использована пороговая фильтрация (7.51) . Это позволило значительно повысить видность полос и уменьшить вклад шумов. Особенно это важно для проблемных областей интерферограммы. Но при этом происходит частичное сглаживание полос и восстановленное изображение становится сильно «размытым». Важно подобрать значение порогового уровня так, чтобы не потерять полезную информацию, заключенную в искривлении полос, и избавиться от шумов и дефектов.
В результате такой предобработки интерферограмм видность полос в местах дефектов повышается (рис. 7.60).
Далее полученное изображение I2(x,y) складывается с исходным I1(x,y) с весовым коэффициентом L2 (0<L2<1) по следующей формуле:
|
|
(7.52) |
Кроме эффекта повышения видности (рис. 7.61,а), суммирование изображений позволяет восстановить ход полос и избавиться от дефекта потери полосы в проблемных местах (рис. 7.61,б).

Рисунок 7.60 – Интерференционная проекция (рис. 4.22а) после предобработки на первом этапе (I2).
|
|
|
| а |
б |
Рисунок 7.61 – Области интерферограммы, представленные на рис. 4.23,
после улучшения их качества.

Рисунок 7.62 – Интерферограмма (рис. 7.58,а) после улучшения ее качества.
Используя предложенный алгоритм, были улучшены 10-ть интерференционных проекций. Затем, используя алгоритм восстановления с 2D фурье-преобразованием, были восстановлены фазовые проекции. На рис. 7.63 представлена фазовая проекция, восстановленная из исходной интерференционной проекции, (рис. 4.58,а) до ее улучшения рис. 7.63,а и после улучшения рис. 7.63,б.
|
|
|
| а |
б |
а б
а) до улучшения интерферограммы (в черных областях нет информации); б) после улучшения интерферограммы
Рисунок 7.63 – Фазовая проекция..
|
|