Широкое внедрение томографии и использование самых различных типов излучения для получения изображения внутренней структуры объектов позволяют считать ее универсальным методом отображения и рассматривать с этой точки зрения в общем, ряду с другими способами получения изображения.
В настоящей главе мы, конечно, не будем сопоставлять томографию со всеми способами отображения информации, а попытаемся выделить некоторые общие черты в голографическом и томографическом методах получения изображения и укажем на их принципиальные отличия. Такой анализ нам кажется полезным и интересным не только с методической точки зрения. Совмещение этих двух методов в конкретной информационно-измерительной системе позволяет решать такие важные для практического применения задачи, как трехмерное отображение внутренней структуры и синтез объемных изображений по набору томограмм. Возможные методы решения указанных задач будут рассмотрены в данной главе. При этом будут анализироваться не только алгоритмы синтеза голограмм математически заданных трехмерных объектов, но и реализация их в оптических системах с преобразованием волнового фронта, т. е. оптический синтез голограмм. Мы покажем также, как взаимное проникновение идей томографии и голографии позволяет решать проблему «скрытых» линий в трехмерных дисплеях и синтезировать оптические копии внутренней структуры объектов.
Многое указывает на тесную связь томографических и голографических методов отображения информации, в первую очередь то, что в обоих случаях исследуемый объект взаимодействует с излучением, которое потом регистрируется. Причем в обоих случаях, как правило, необходимо измерить амплитуду и фазу поля. Нужно отметить, что голографическая регистрация применяется в томографических исследованиях давно, достаточно вспомнить голографическую интерферометрию, дисдрометрию и т. д. Следующий шаг — восстановление из зарегистрированной информации (поля) изображения объекта. Заметим, что в обоих случаях решается обратная задача. То есть как голография, так и томография представляются собой двухступенчатый процесс, на втором этапе которого реализуется некоторый обратный оператор. Особенности этого оператора и составляют отличие методов.
В голографии рассматривается схема получения информации в трехмерном объекте, расположенном в однородной среде, и излучение взаимодействует только с внешними его границами. В этом случае принято считать, что решается уравнение Гельмгольца, описывающее процесс распространения поля в пространстве при наличии распределения токов на некоторой поверхности L. Решение этого уравнения можно найти, используя теорему Грина, тогда выражение для каждой декартовой составляющей поля в точке p на плоскости голограммы будет иметь вид
![]() (4.1)
(4.1)
где r' –радиус-вектор точки на поверхности L; r –радиус-вектор точки наблюдения; n – внешняя нормаль к поверхности объекта; t(r') и ![]() - распределение значений поля и его нормальной производной на поверхности тела;
- распределение значений поля и его нормальной производной на поверхности тела; ![]() - функция Грина;
- функция Грина; ![]() - волновое число.
- волновое число.
Преобразуем (4.1), учитывая, что геометрические параметры голографической схемы и разрешающий интервал в восстановленном изображении, в пределах которого t(r') мало меняется, много больше длины волны. Тогда выражение для поля на голограмме может быть описано следующим выражением:
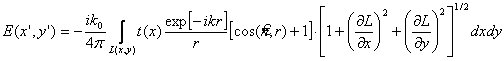 (4.2)
(4.2)
Здесь x, y, z – оси координат в области задания объекта с началом в точке ![]() ;
; ![]() - уравнение поверхности объекта; x', y' – координаты точки на голограмме, отстоящей на расстояние z0 от объекта.
- уравнение поверхности объекта; x', y' – координаты точки на голограмме, отстоящей на расстояние z0 от объекта.
![]()
Выражение для r может быть представлено в виде ряда:
![]() (4.3)
(4.3)
Группируя члены, не зависящие от ![]() , полагая, что
, полагая, что
![]() (4.4)
(4.4)
выражение для r можно переписать в виде
![]()
где
![]()
Для тех случаев, когда косинус угла между нормалью к поверхности объекта в данной точке и направлением распространения волны мало меняется в пределах голограммы, т.е. при условии наблюдения объекта под некоторым определенным углом (ракурсом), можно записать
![]() (4.5)
(4.5)
![]()
![]() - координаты центра голограммы.
- координаты центра голограммы.
Учитывая (4.4) и (4.5), выражение для поля на голограмме можно записать в виде свертки:
 (4.6)
(4.6)
Нетрудно заметить, что при известном поле на голограмме выражение (4.6) представляет собой интегральное уравнение Фредгольца первого рода типа свертки с ядром ![]() . Решение этого уравнения, т. е. определения поля в области объекта по измеренному полю на голограмме, представляет собой обратную, задачу. Уравнения типа свертки решаются, как правило, с использованием преобразования Фурье.
. Решение этого уравнения, т. е. определения поля в области объекта по измеренному полю на голограмме, представляет собой обратную, задачу. Уравнения типа свертки решаются, как правило, с использованием преобразования Фурье.
Рассмотрим подынтегральное выражение. Оно представляет собой произведение двух функций. Первая функция
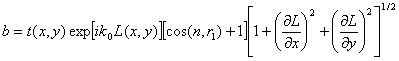
содержит практически всю информацию об объекте, несмотря на свою двухмерность. Здесь t(х',у') — амплитуда, которая слабо меняется при переходе от поверхности объекта к плоскости х, у в области объекта; ![]() определяет форму поверхности;
определяет форму поверхности; ![]() — ракурс, под которым наблюдается объект. Вторая подынтегральная функция
— ракурс, под которым наблюдается объект. Вторая подынтегральная функция

характеризует геометрические параметры голографической схемы.
Из анализа (4.6) можно сделать вывод, что при выбранных условиях на размеры объекта и геометрические параметры голографической схемы (неравенство (4.4)) изображение объекта представляет собой двумерную функцию (в нашем случае). Это значит, что измеренных данных Е(х', у') должно хватить для решения интегрального уравнения (4.6). Изменяя ракурс, т. е. вектор r1 в ![]() , можно получить изображение объекта под другим углом φ, так как в этом случае преобразуется относительно объекта вся схема измерения поля Eφ.
, можно получить изображение объекта под другим углом φ, так как в этом случае преобразуется относительно объекта вся схема измерения поля Eφ.
Для решения уравнения (4.6) относительно q по известной функции Е(х', у') воспользуемся, теоремой о фурье-образе свертки:
![]() (4.7)
(4.7)
После несложных преобразований получим
Ё ![]() (4.8)
(4.8)
Перечислим операции, которые необходимо выполнить для реализации алгоритма, описываемого формулой (4.8):
1) вычислить Фурье-образ на голограмме ![]() ;
;
2) вычислить фурье-образ от функции распространения ![]() ;
;
3) разделить ![]() на
на ![]() ;
;
4) выполнить обратное преобразование Фурье.
В этом алгоритме при его реализации на ЭВМ необходимо выполнять регуляризацию, которая обусловлена некорректностью задачи. Учитывая, что функция q1 радиально-симметричная ![]() преобразуем
преобразуем ![]() к следующему виду:
к следующему виду:
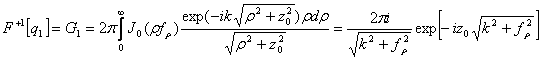 (4.9)
(4.9)
![]()
Тогда выражение (4.8) примет вид
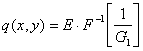
Из условий (4.4) и (5,5) следует, что пространственный спектр объекта достаточно узок. В этом случае с точностью до амплитудной функции ![]() , G1 можно преобразовать таким образом, что
, G1 можно преобразовать таким образом, что
 (4.10)
(4.10)
Таким образом, в показателе экспоненты в пропагаторе сменится знак. Тогда восстановленное изображение запишем в виде
![]() (4.11)
(4.11)
Алгоритм восстановления, представленный в таком виде, чрезвычайно удобно реализовать в оптическом процессоре, так как выражение (4.11) описывает дифракционное поле от голограммы в области изображения.
Таким образом, восстановление поверхности трехмерного объекта возможно как на ЭВМ, так и в оптике. В обоих случаях реализуется решение интегрального уравнения первого рода. В случае оптического восстановления алгоритм реализуется, чрезвычайно просто и красиво, что, очевидно, и обусловило его широкое распространение на практике. Восстановление на ЭВМ в оптическом диапазоне не нашло применения, хотя на такую возможность для простейших случаев голографии (Фурье, Френеля) Д. Гудмен указал еще в
Наиболее близко, на наш взгляд, с голографией связаны методы дифракционной томографии. Помимо чисто схемных совпадений, таких, как многоракурсное освещение (зондирование) объекта, регистрация рассеянного поля голографическим способом, накопление информации и последующее восстановление, существует и глубокая связь, заключающаяся в том, что в обоих случаях решается задача обращения поля, рассеянного объектом. Однако различие в исследуемых характеристиках объектов и, как следствие, особенности алгоритмов обработки разделили эти методы. В голографии простота оптической реализации восстановления практически вытеснила цифровое восстановление голограмм. Успехи компьютерной томографии, в свою очередь, сузили область применения оптического восстановления изображений внутренней структуры.
Отметим основные задачи, возникающие при восстановлении томограммы, которых нет в голографическом отображении информации. Прежде всего, голограмма, полученная под одним ракурсом, позволяет однозначно восстановить трехмерное изображение. При увеличении числа ракурсов только расширяется поле зрения и возникает эффект кругового обзора. При этом каждая голограмма отвечает за свой участок объекта. В томографии для восстановления принципиально необходимо многоракурсное зондирование, так как размерность проекции всегда меньше восстанавливаемой функции (в нашем случае одномерная проекция Е'(х') — двумерный объект ε(х, у)). Для получения томограммы необходимы все проекции одновременно, так как каждая из них участвует в восстановлении сечения. По-видимому, это принципиальное отличие голографии от томографии, которое порождает основные трудности при оптической реализации восстановления внутренней структуры объекта. Наиболее важные среди них — пространственная фильтрация проекций и суммирование преобразованных проекций.
Мы сделали попытку сопоставить и сблизить различные способы реализации алгоритма восстановления в томографии и голографии и показать, что выбор наиболее оптимальной схемы определяется конкретной задачей. В частности, для оптических исследований оптическое восстановление в томографии, как указывалось ранее, представляет большой интерес, что не исключает использование ЭВМ на стадии обработки восстановленного изображения.
Развитие вычислительной техники выдвинуло в качестве одной из наиболее важных задач разработку методов представления результатов расчета в виде изображений. В этой связи большой интерес представляет использование синтезированных голограмм для визуализации трехмерных сцен, которые позволяют на плоскости закодировать информацию о трехмерном изображении. Такими изображениями могут быть результаты расчета трехмерных функций, пространственные диаграммы направленности антенн, вычисленные на ЭВМ формы различных объектов (макеты молекул, детали автомобилей), данные сейсморазведки и др. Задача в такой постановке возникла практически сразу же после появления цифровой голографии, тем не менее, она до сих пор не решена и в настоящее время практически не рассматривается. Дело, видимо, в том, что с отображением формы объектов, стали достаточно успешно справляться графические дисплей, связанные с большими ЭВМ. Ситуация, должно быть, изменилась в пользу голографии только с появлением необходимости строить трехмерные изображения внутренних структур. Современные компьютерные, рентгеновские, УЗВ-, ЯМР-томографы позволяют определять распределение искомой величины внутри объекта в десятках сечений, что привело к резкому росту объема информации, представленной в виде изображений. Последовательное наблюдение данных сечений снижает их диагностическую ценность, поэтому возникла острая необходимость в трехмерном отображении хранимой информации. Фактически задача состоит в разработке долговременной памяти трехмерных изображений, причем такая память должна обладать свойствами архива большой емкости и трехмерного дисплея. Естественно, что к решению указанной задачи обратились специалисты, занимающиеся голографией, которая по своим потенциальным возможностям отвечает указанным требованиям. Необходимо отметить еще одну важную особенность томографической информации, которую мы неоднократно подчеркивали. Она является результатом решения обратной задачи, которую можно решать как в оптическом, так и цифровом процессоре. Это позволяет видоизменять томографический алгоритм таким образом, чтобы, например, облегчить последующую голографическую регистрацию томограммы. Далее мы покажем, как такое взаимное проникновение методов позволяет решить проблему затенения одного сечения другими.
Мы не будем затрагивать вопросы, связанные с архивной голографической памятью трехмерных изображений. Остановимся только на возможности использования голографии для трехмерного отображения томографической информации, хранящейся в ЭВМ. При анализе трехмерных внутренних структур, как правило, рассматривают две задачи. Первая связана с отображением формы органов как некоторых фигур, вторая — с синтезом трехмерных изображений из набора томограмм (сечений). В соответствии с данными задачами и рассмотрим различные алгоритмы синтеза голограмм.
При синтезе голограмм произвольных объектов основной вычислительной операцией является расчет поля от объекта на голограмме. В пункте 4.1 анализировался процесс формирования поля, рассеянного трехмерным объектом, в плоскости регистрации. Такое описание соответствует первой задаче, когда необходимо наблюдать лишь форму объекта. Уравнение поля на голограмме в анализируемом случае описывается выражением (4.6).
В тех случаях, когда объем голографируемой сцены таков, что неравенство (4.4) не удовлетворяется, выражение (4.6) можно использовать, если представить объект в виде набора сечений, расположенных на разных расстояниях от плоскости голограммы. При этом в области каждого сечения объект разбивается на зоны, в пределах которых описывается выражением L(x,y). Поле от каждой зоны вычисляется по формуле (4.6).
Для второго случая объект представляется в виде набора сечений. При такой модели объекта естественно воспользоваться для описания поля в плоскости голограммы интегралом Кирхгофа, который для квазиоптического случая имеет вид:
![]() (4.12)
(4.12)
где ху — плоскость транспаранта; t — комплексная функция рассеивания транспаранта; n — нормаль к транспаранту; r — расстояние от точки наблюдения р до точки на транспаранте.
Вычисление интегралов (4.6), (4.12) позволяет определять значение поля от объекта на поверхности голограммы.
Для расчета интегралов (4.6), (4.12) в вычислительной математике применяются, например, методы Гаусса, Лонгмана, Филона и метод замены интеграла интегральной суммой. Последний позволяет существенно сократить время расчетов на ЭВМ. Поэтому в дальнейшем рассматривается только метод интегральных сумм, согласно которому интеграл (4.12) заменяется суммой. В дальнейших преобразованиях рассмотрим выражение для поля от транспаранта, т. е. формулу (4.12), так как преобразования выражений (4.6) и (4.12) аналогичны.
Заменяя в (4.12) интеграл интегральной суммой, получаем:
![]() (4.13)
(4.13)
Такое представление интеграла имеет следующие физический смысл: объект моделируется дискретным набором из т точек, имеющих комплексный коэффициент рассеяния tj и находящихся на расстоянии rj от точки р на голограмме. Расстояние между точками на объекте в общем случае изменяется в пределах объекта в зависимости от его сложности. В частном случае оно может быть постоянным (эквидистантное представление объекта).
Однако подобное представление, как заметил Д. Габор, не соответствует реальной физической картине. Действительно, реальная голографическая система имеет конечную апертуру и конечный интервал разрешения, т. е. голограмма «видит» объект, представленный не в виде набора точечных источников, а в виде набора пятен, размер которых зависит от разрешающей способности голограммы. Наиболее целесообразно использовать для представления функции рассеивания каждого элемента разрешения функцию Гаусса:
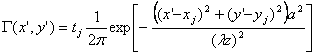 (4.14)
(4.14)
где xj, уj — координаты элемента разрешения; а — апертура голограммы; z — расстояние от плоскости голограммы до транспаранта. Функция Г(х', у') нормирована таким образом, чтобы интеграл от нее был равен коэффициенту рассеивания в данной точке. Подставив выражение (4.14) в (4.13), получим формулу для вычисления поля от объекта:
 (4.15)
(4.15)
Представление объекта в виде «гауссовых пятен» приводит к существенному улучшению качества восстановленного изображения. Если при расчете голограммы расстояние между точками объекта выбиралось меньше разрешающего интервала голограммы, то при оптическом восстановлении получаем сплошное изображение объекта.
В зависимости от различных параметров голографической схемы возможно существенно упростить вычисление дифракционной картины.
Для анализа воспользуемся выражением для поля в плоскости голограммы от плоского объекта (4.12). Некоторые упрощения этого выражения возможны при различных аппроксимациях показателя экспоненты:
![]()
Для этого воспользуемся следующим разложением в ряд величины r:
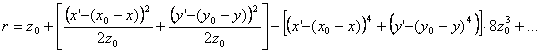
В теории дифракции обычно вводят зоны дифракции или приближения Френеля и Фраунгофера. В качестве приближения Френеля принимается такое, при котором для аппроксимации показателя экспоненты достаточно ограничиться первыми двумя членами разложения.
В области дифракции Фраунгофера в разложении r можно пренебречь квадратичными членами и членами более высоких порядков. При выборе той или иной формулы для расчета поля от объекта на голограмме необходимо установить границы применения различных аппроксимаций и оценить влияние подобных приближений на качество восстановленного изображения. Для этого выведем точные количественные соотношения, связывающие параметры голографической схемы и поле от объекта.
Для оценки качества восстановленного изображения используем четкость по Стрелю, т. е. отношение интенсивностей в центре дифракционного пятна при наличии приближений, и в идеальном случае ![]() . Рассмотрим простейшую голографическую схему. Объект представляет собой две точки единичной амплитуды с координатами
. Рассмотрим простейшую голографическую схему. Объект представляет собой две точки единичной амплитуды с координатами ![]() .
.
Если при восстановлении использовать тот же опорный пучок, что и при записи, и рассматривать поле в области формирования мнимого изображении, то после ряда преобразований получим выражение для поля мнимого изображения:
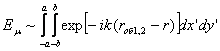
где Еμ — поле мнимого изображения, 2а×2b — апертура голограммы по x' и y' соответственно:
![]()
![]()
ζ, η — система координат в области формирования мнимого изображения с началом в точке с координатами x0, y0, z0.
Допустим, что в процессе синтеза мы не можем пренебречь квадратичными, но пренебрегаем членами более высоких порядков, тогда, разлагая rоб1,2 в ряд и обозначая через r'oб1,2 те значения, при которых вычислялось поле от объекта, получаем
![]()
Для оценки влияния приближений необходимо сравнить выражения для поля в отсутствие и при наличии искажений. В первом случае в области формирования мнимого изображения значения roб1,2 и r совладают, во втором случае в показателе экспоненты под интегралом появляются слагаемые, который не компенсируются при восстановлении. После ряда преобразований выражение для поля мнимого изображения в точке ![]() при использовании на стадии синтеза голограмм френелевского приближения можно представить в виде:
при использовании на стадии синтеза голограмм френелевского приближения можно представить в виде:
![]() (4.16)
(4.16)
а интенсивность равна
![]()
В отсутствии искажений, т. е. когда синтезированная голограмма вычисляется без каких-либо искажений, интенсивность восстановленного изображения при ![]() соответствует
соответствует
![]()
В оптике принято считать, что качество изображения удовлетворительно, если |D-1|≤0.2, т. е. необходимо, чтобы

Из (4.16) легко получить условия, которые необходимо накладывать на z0 - расстояние между плоскостью голограммы и плоскостью объекта, чтобы удовлетворялась четкость по Стрелю:
![]() (4.17)
(4.17)
Неравенство (4.17) дает границу снизу для зоны Френеля для определения верхней границы зоны Френеля (нижней границы зоны Фраунгофера) необходимо провести выкладки, аналогичные вышеприведенным, но при этом в выражении (4.16) нужно пренебречь также и квадратичными членами. В этом случае верхняя граница зоны Френеля
![]()
Таким образом, используя в качестве критерия удовлетворительного качества изображения неравенство |D—1|<0,2, получаем следующие условия для выбора представления поля от объекта в зависимости от параметров голографической схемы:
ближняя зона:
![]() (4.18)
(4.18)
зона Френеля:
![]()
(4.19)
зона Фраунгофера:
![]() (4.20)
(4.20)
Основным недостатком алгоритма вычисления голограмм является быстрый рост машинного времени с увеличением числа точек в объекте и на голограмме. Известно, что возможно представление интеграла Кирхгофа через ДПФ. Это позволяет использовать для вычисления интеграла Кирхгофа алгоритм БПФ, что приводит к сокращению числа комплексных операций умножения с N2 в случае прямого вычисления интеграла Кирхгофа до Nlog2N.
При использовании ДПФ для вычисления синтезированных голограмм в целях уменьшения используемого машинного времени целесообразно рассматривать три алгоритма вычисления поля от объекта в плоскости голограммы в зависимости от области дифракции, в которую мы помещаем голограмму.
Приближение Фраунгофера. Расчет дифракционной картины существенно упрощается в случае приближения Фраунгофера, т. е. когда расстояние от объекта до плоскости голограммы удовлетворяет неравенству (4.20). В этом случае поле от каждого транспаранта либо сечения объекта, расположенного и плоскости, параллельной плоскости голограммы, можно представить в вида интегральной суммы. Учитывая множитель 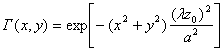 , позволяющий представлять объект в виде набора «гауссовых пятен», получаем следующую формулу для вычисления поля на голограмме от одной плоскости объекта:
, позволяющий представлять объект в виде набора «гауссовых пятен», получаем следующую формулу для вычисления поля на голограмме от одной плоскости объекта:
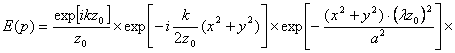
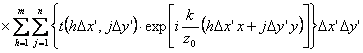
где m и n — число точек, на объекте по осям x' и у' соответственно.
Это выражение представляет собой дискретное преобразование Фурье, которое эффективно обрабатывается на ЭВМ с помощью алгоритма БПФ. Затем, произведя суммирование полей от различных транспарантов либо сечений объекта, получает поле от объекта в плоскости голограммы.
Приближение Френеля. В случае приближения Френеля расстояние от плоскости голограммы до объекта должно удовлетворять неравенству (4.19).
Представляя объект, как и ранее, в виде набора сечении или транспарантов, расположённых по глубине, будем вычислять дифракционное поле от объекта в виде суммы дифракционных полей от всех плоскостей. Интеграл Кирхгофа от одной из плоскостей преобразуется в приближении Френеля с учетом множителя, позволяющего представлять объект в виде «гауссовых пятен», к виду
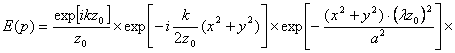

Данное, выражение представляет собой двумерное ДПФ от матрицы tk,j умноженной на множитель 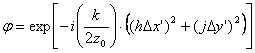 . Таким образом, как и в предыдущем случае, для вычисления поля от одной плоскости объекта на голограмме достаточно однократного применения БПФ.
. Таким образом, как и в предыдущем случае, для вычисления поля от одной плоскости объекта на голограмме достаточно однократного применения БПФ.
Для нас наибольший интерес представляет случай ближней зоны дифракции, которому соответствует неравенство (4.18). При данном ограничении на z0 для вычисления используется выражение (4.12).
Выражение (4.12) представляет собой свертку двух функций: комплексной функции рассеивания в плоскости ху t(x, у) и ![]() .
.
Для вычисления интеграла (4.12) воспользуемся теоремой о фурье-образе свертки:
![]() (4.21)
(4.21)
Здесь F+1 означает прямое преобразование Фурье.
Для вычисления фурье-образов функций t(x',y') и ![]() q(x',y') необходимо представить их в виде матриц комплексных чисел, а затем вычислить ДПФ, используя алгоритм БПФ. Затем по формуле (4.21) вычисляется фурье-образ поля от объекта на голограмме. Однако в целях сокращения машинного времени для некоторых частных случаев возможно вычисление фурье-образа функции q(x', у') с помощью аналитического соотношения.
q(x',y') необходимо представить их в виде матриц комплексных чисел, а затем вычислить ДПФ, используя алгоритм БПФ. Затем по формуле (4.21) вычисляется фурье-образ поля от объекта на голограмме. Однако в целях сокращения машинного времени для некоторых частных случаев возможно вычисление фурье-образа функции q(x', у') с помощью аналитического соотношения.
Полагая, что косинус угла между нормалью к сечению объекта и направлением распространения волны мало меняется в пределах голограммы, выражение (4.21) преобразуем к виду :
![]() (4.22)
(4.22)
где
![]() ;
;

Используя формулу (4.9), можно вычислить фурье-образ q1(x',у') аналитически, что сокращает затраты машинного времени на расчет поля от объекта на 25…30%.
Таким образом, для вычисления ![]() достаточно вычисления фурье-образа из функции t1(x’, y’). Далее, используя алгоритм обратного преобразования Фурье, легко можно определить поле от объекта на голограмме:
достаточно вычисления фурье-образа из функции t1(x’, y’). Далее, используя алгоритм обратного преобразования Фурье, легко можно определить поле от объекта на голограмме:
![]()
Покажем возможность вычисления голограмм трехмерных объектов с использованием рассмотренных алгоритмов. Ограничимся случаем отображения формы объекта. Тогда можно считать, что объект задан в виде карты изолиний, т. е. для его задания не требуется большого количества информации.
Для расчета голограммы воспользуемся алгоритмом ближней зоны дифракции, описываемым формулами (4.12) и (4.22). Перепишем указанный алгоритм в виде следующей последовательности операций:
1) вычисление функции t1;
2) вычисление фурье-образа функции t1
![]()
3) вычисление фурье-образа аподизирующей функции:
![]() (4.23)
(4.23)
4) вычисление фурье-образа функции распространения (4.9):
![]() (4.24)
(4.24)
5) вычисление фурье-образа поля на голограмме:
![]() (4.25)
(4.25)
6) вычисление поля на голограмме
![]() (4.26)
(4.26)
7) вычисление Еоп
8) вычисление голограммы
![]()
9) построение голограммы
Из анализа алгоритма видно, что для расчета фурье-образа поля на голограмме достаточно однократного использования БПФ для вычисления
![]()
Нетрудно заметить, что функция q1 зависит только от геометрических параметров схемы и определяет фокусирующие свойства голограммы, поэтому вычисление этой функции необходимо производить на всей апертуре голограммы. Функция t1 определяет информационную часть поля. Число отсчетов и апертура, в которых необходимо вычислять эту функцию, определяются требуемой разрешающей способностью. Эта апертура, как правило, много меньше той, которая необходима для хорошей фокусировки объекта. Поэтому для определения поля на больших голограммах F+l [t1] можно вычислять на части требуемой апертуры, а затем мультиплицировать на остальные участки.
При визуализации трехмерных объектов, заданных в виде карт изолиний, число элементов разрешения (число отсчетов, в которых задана матрица t1 ) в сечении, параллельном плоскости голограммы, как правило, невелико. Известно, что при использовании БПФ число отсчетов в образе и фурье-образе одинаково. Таким образом, для вычисления фурье-образа поля от объекта на голограмме достаточно вычислить БПФ от матрицы, содержащей порядка 104 отсчетов (операция 2). Для вычисления голограмм с большими апертурами может быть использовано свойство периодичности коэффициента Фурье, что позволяет мультиплицировать эти коэффициенты и получать затем голограмму с большой апертурой. Полученную таким образом матрицу коэффициентов Фурье для вычисления F+1[E] необходимо домножить на функции (4.23) и (4.24).
При расчете поля от объекта на голограмме необходимо вычислить обратное преобразование Фурье от матрицы F+1[E]. Число отсчетов, в которых задана эта матрица, равно числу выборок на; голограмме. При визуализации трехмерных изображений это число должно быть велико (106 отсчетов). Вычисление БПФ от функции, заданной таким количеством отсчетов, на ЭВМ требует значительных затрат машинного времени и практически не представляется возможным. Его целесообразно производить оптически. Для этого на ЭВМ вычисляется интерференция F+1[Е] с плоской волной Eоп = ехр[—ifx/k×sina], и с использованием устройства вывода изображений из ЭВМ (в экспериментах использовалось устройство УОГ-2) выводится на фотопленку следующая функция:
![]()
где звездочка означает комплексное сопряжение.
![]()
Затем фотопленка уменьшается в требуемое число раз n устанавливается в переднюю фокальную плоскость линзы. Фотопленка освещается Восстанавливающей волной, эквивалентной Еоп, и в задней фокальной плоскости на ее оси формируется спектр четвертого слагаемого, который описывается следующим выражением:
Фурье-образ Еоп представляет собой d-функцию. Таким образом, в фокальной плоскости линзы фокусируется поле Е, которое формирует восстановленное изображение.
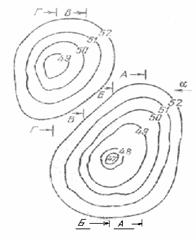
Разработанный алгоритм использовался для экспериментов по визуализации трехмерных объектов, заданных в виде карт изолиний (рисунок 4.1). В качестве объекта было выбрано два холма различной высоты и формы. После ввода в ЭВМ структурная карта представлялась в виде набора из четырех сечении (А, Б, В, Г), причем в области каждого сечения объект разбивался на зоны, в пределах которых поле от него описывается выражением (4.6). От каждой зоны независимо вычислялся фурье-образ поля на голограмме, при этом учитывался только эффект «затенения» одной части тела другой. Затем фуръе-образы суммировались. На рисунке 4.2 представлено изображение, восстановленное оптически с синтезированной голограммы. В каждом сечении задавалось 128x128 точек отсчета. Голограмма вычислялась в 1024x1024 точках.
 |
 |
Рисунок 4.2 – Изображение, восстановленное с синтезированной голограммы
Основным элементом голографического дисплея, предназначенного для визуализации трехмерных образов, сведения о конфигурации которых хранятся в памяти ЭВМ, описанного выше, является синтезированная голограмма. Применение синтезированных голограмм в системах отображения сдерживается следующими основными причинами: во-первых, устройства вывода изображений не позволяют строить голограммы с высокими пространственными частотами; во-вторых, необходимы затраты большого количества времени ЭВМ для вычисления голограмм с высокой информационной емкостью. В связи с этим представляется более рациональным сочетание приемов цифрового и оптического синтеза голограмм.
Рассмотрим основные принципы построения оптического процессора, который позволяет вычислить и построить голограмму, способную сформировать неискаженное трехмерное изображение математически заданного объекта. Процессор работает по алгоритму синтеза голограмм, подробно описанному в пункте 4.3.1.
При анализе указанного алгоритма отмечалось, что введение в него мультипликации спектра функции существенно упрощает вычислительную процедуру. Учитывая данное замечание, алгоритм вычисления голограмм можно свести к следующей последовательности операций:
1) вычисление функции t1;
2) вычисление F+1 [t1];
3) мультиплицирование MF+1 [t1];
4) вычисление F+l[q1] (здесь и далее ; x0 = y0 = 0);
5) F+1{E] = F+1 (q1)MF +1 [t1];
6) E = F-1[F+1 [q1]MF+1[t1]];
7) вычисление Eоп;
8) I = /Е + Еоп/2 ;
9) построение голограммы.
Несложный анализ показывает, что все операции кроме 1 и 4 могут быть реализованы в оптическом процессоре. Операция 1 реализуется на ЭВМ, операция 4 реализуется аналитически.
Принципиальная схема этого процессора представлена на рисунке 4.3.
После вычисления t1 результат поступает на вход оптической части процессора, где t1 отображается управляемым транспарантом Т1, который освещается когерентным светом с плоским волновым фронтом. Угловой спектр модулированного управляемым транспарантом излучения мультиплицируется по заданному закону устройством У. Линза Л1 выполняет фурье-преобразова-ние излучения, прошедшего через транспарант и мультипликатор.
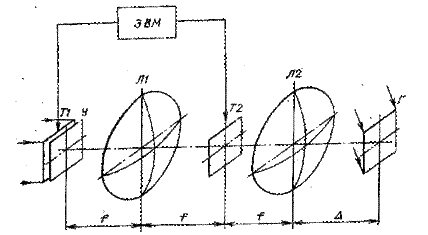
Рисунок 4.3 – Принципиальная схема оптической системы синтеза голограмм
Следовательно, в фокальной плоскости Л1 перед маской Т2 распределение комплексных амплитуд поля имеет вид MF+1 [t1]. Результат вычисления F+l [q1] поступает в процессор в виде маски Т2 в заднюю фокальную плоскость линзы Л1. За маской Т2 ам-; плитуда поля имеет вид F+l[q1]F+l[t1]. Линза Л2 выполняет ; обратное фурье-преобразование излучения, прошедшего через маску Т2. Таким образом, в процессоре выполняются все вышеперечисленные операции. На голограмме Г происходит накопление изображения объемной сцены. С этой голограммы после обработки восстанавливают трехмерное изображение.
Однако вычисление и построение F+1 [q1] в виде амплитудно- фазовой маски требует наличия совершенного устройства вывода либо управляемого транспаранта с высоким разрешением (1000 лин./мм). Для того чтобы обойти эту трудность, можно несколько видоизменить алгоритм и свести его к следующей последовательности операций:
1') вычисление функции t1
2') F+1[t1];
3') мультиплицирование MF +1 [t1];
4') вычисление функции q1 = exp(ikr0’)/r0’; r'0 = [(х-х'-хоп)2+(у-у’)2+ z0’]2',
5') F+1[q1] = F+1 [q1] ехр (—ikxfxоп/f);
6') регистрация промежуточной голограммы
![]()
![]()
8') ![]()
9') I= ½E + Eоп ½2;
10') построение голограммы.
Здесь звездочка означает комплексное сопряжение; Xf — текущая координата в плоскости Г1; f — фокальный отрезок линз Л1 и Л2; х0„ — сдвиг функции фокусировки.
голограмма Г1 выполняет операцию вычисления I; линза Л2 - операцию вычисления E; голограмма Г2 регистрирует и визуализирует изображение.
Нетрудно заметить, что последние две операции (9" и 10') алгоритма могут не выполняться, так как достаточно одного регистратора в фокальной плоскости Л1. Схема оптического процессора, представленная на рисунке 4.4, была проверена экспериментально. Вычисление поля в макете процессора исследовалось на моделях геологических объектов. Математические модели представляют собой карты изолиний двух холмов различной формы и высоты. Каждый холм задан набором из трех сечений. Каждое сечение имеет слабо выраженный рельеф. Фронтальное сечение более удаленного холма располагается дальше от наблюдателя, чем последнее сечение менее удаленного. Поперечные размеры каждого из холмов находятся в пределах 50x60 мм, а поперечные размеры всей карты— 110x60 мм.
Для проведения эксперимента были изготовлены физические модели. Все сечения, кроме фронтальных, аппроксимировались плоскими прозрачными участками на транспарантах, причем каждому сечению соответствовал отдельный транспарант. Фронтальные сечения были выполнены в виде рельефных диффузно отражающих поверхностей.
К элементам Л1 и Л2 схемы предъявляются особые требования. Для обеспечения удовлетворительных условий наблюдения трехмерного изображения описанной выше модели указанные линзы должны сочетать значительные поперечные размеры с большим относительным отверстием (1 : п> 1 : 2,5). В эксперименте была использована линза Л1 со следующими параметрами: f =
Регистрация голограммы Г1 осуществлялась последовательно, каждое сечение регистрировалось за одну экспозицию. Сечение при экспонировании размещалось в передней фокальной плоскости Л1, как это показано на рисунке 4.4, причем прозрачные сечения освещались через диффузный рассеиватель, а отражающие сечения освещались нерассеянным лазерным светом. Мультипликация углового спектра поля (операция 3' алгоритма) осуществлялась, следовательно, путем диффузного освещения сечения либо диффузного отражения от поверхности сечения. В данном случае не требуется специальное устройство, мультиплицирующее угловой спектр поля (устройство У на рисунке 4.3).
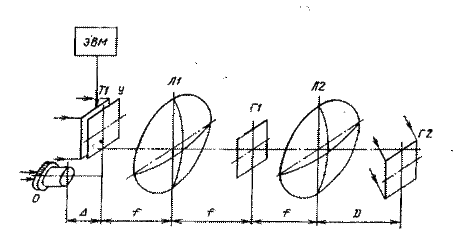
Рисунок 4.4 – Оптическая схема для синтеза голограмм по набору транспарантов
Микрообъектив О для регистрации отдельного сечения выставлялся таким образом, что сформированный им точечный источник при постоянных поперечных координатах имел продольную координату, равную удалению, которое должно было бы иметь данное сечение в изображении. Поскольку расстояние между соседними сечениями было принято равным
Голограмма Г1 восстанавливалась наклонным параллельным лазерным пучком (операция 1' алгоритма). В результате в первом порядке дифракции непосредственно за голограммой восстанавливалась волна, распределение амплитуд в которой соответствовало произведению мультиплицированного фурье-образа функции сечения и фурье-образа функции фокусировки. Линза Л2, посредством которой осуществлялось фурье-преобразование восстановленного с голограммы Г' 1 излучения, идентична линзе Л1.
Для оценки результатов вычисления поля в макете оптического процессора не было необходимости регистрировать голограммы на выходе процессора. Трехмерное изображение наблюдалось за задней фокальной плоскостью линзы Л2. Глубина восстановленного изображения при поперечных размерах 110x60 мм составляла
Проведенные исследования показывают возможность создания голографического дисплея на основе оптического процессора для визуализации математически заданных объектов, при обработке геофизической информации, в медицине, навигации и при обучении.
Проверка на характерные для голографических изображений при изменении масштаба аберрации — астигматизм и кривизну поля — показала, что в пределах точности измерений указанные аберрации отсутствуют.
С развитием топографической техники формирование трехмерного изображения внутренней структуры выдвигается как одна из важных и перспективных задач. К решению ее подключились специалисты не только в области машинной графики, но и оптики. Нетрудно сформулировать требования к трехмерному дисплею для томографии. Они сводятся к необходимости выполнения в устройстве следующих условий:
1. Наблюдение изображения каждого сечения в отдельности и наличие произвольного набора томограмм. Это позволит наблюдателю, во-первых, последовательно «заглядывать» внутрь объекта и, во-вторых, локализовать интересующую их зону. Фактически выполнение данного условия решает вопрос с архивом томограмм;
2. Визуализация изображения сечения произвольной ориентации в пространстве. Выполнение данного условия позволит наблюдателю оперативно менять угол зрения и осуществлять репроекцию трехмерного изображения с целью измерения параметров отдельных включений;
3. Устранение эффекта затенения. Суть этого явления состоит в том, что изображения ближайших сечений закрывают изображения последующих. При построении изображений слабо насыщенных информацией объектов (карт изолиний) указанный эффект проявляется в виде скрытых линий, когда трудно отличить, в какой плоскости лежит та или иная структура;
4. Обеспечение обзора с широким углом зрения внутреннего локального включения, изображение которого построено на ЭВМ. Данное требование относится к задаче визуализации формы объекта, которая рассматривалась в пункте 4.3.
Первые три условия соответствуют задаче синтеза трехмерной оптической модели объекта из двумерных сечений, т, е. задаче, в некотором смысле, обратной томографии.
Мы не будем обсуждать достоинства и недостатки различных методов решения этой задачи, рассмотрим только возможность синтеза трехмерного изображения из набора томограмм в голографическом дисплее, описанном выше. В качестве исходных данных были выбраны реальные томограммы головы, полученные на рентгеновском вычислительном томографе. Голограмма формировалась методом оптического синтеза, который основан на голографической последовательной записи диффузного фурье-спектра каждой томограммы с опорным волновым фронтом, распределение которого в плоскости регистрации является фурье-образом сферической волны с переменным радиусом кривизны. Восстановление осуществлялось путем обратного преобразования Фурье волны, полученной при освещении голограммы плоской волной. Оптическая схема дисплея и ее подробное описание приведены в пункте 4.3.2.
Регистрировалась голограмма пяти транспарантов, расстояние между сечениями выбиралось равным
Экспериментально была проверена возможность наблюдения сечений, ориентированных под углом к исходным томограммам. Для этого в область формирования изображения вводился экран, который произвольно ориентировался в пространстве. Эффект выделения изображения в плоскости экрана наблюдался слабо, что обусловлено малым числом сечений.
Эксперименты показали главный недостаток такой визуализации объемного изображения из набора томограмм — эффект затенения ближайшими томограммами дальних сечений. Если в экспериментах с буквами и «холмами» данный эффект был слабо выражен, то при визуализации таких сложно структурированных изображений, как томограммы, он практически подавил всю наблюдаемую картину.
Эффект затенения отмечался неоднократно, и предлагались различные методы его устранения. В настоящее время в качестве решения предлагается последовательное представление сечений и формирование их изображений с помощью зеркала с переменным фокусным расстоянием. Интерактивная работа с таким дисплеем позволяет в некотором смысле решить задачу наблюдения незатененного сечения. Очевидно, что такое решение не подходит для голографического дисплея.
Эксперименты по инверсной томографии показывают, что использование голографических методов в томографии не приносит существенных результатов, если при построении конкретных приборов не учитывать общих черт обоих методов исследования объекта, основанных на решении обратной задачи рассеяния. Рассмотрим принципиальную возможность построения оптической системы, совмещающей оба метода для решения задачи получения световых копий внутренней структуры объектов или топографической томографии. Анализ будем проводить на примере задачи инверсной томографии, при этом покажем возможность устранения эффекта затенения.
Рассмотрим более подробно процесс наблюдения трехмерного изображения, представленного в виде набора световых копий томограмм. Пусть в пространстве формируется последовательность изображении сечений fk(x,z), фокусирующихся на различных расстояниях от голограммы. Будем наблюдать изображение, восстановленное под углом φi в некоторой плоскости xz, расположенной на расстоянии уk от голограммы. В приближении геометрической оптики поле в указанной плоскости можно представить как сумму полей, формируемых в различных плоскостях:
![]() (4.27)
(4.27)
где М — число томограмм;
k — номер томограммы;
уk — расстояние от k-ой томограммы до плоскости наблюдения.
Координату z, которая должна входить в данное выражение как параметр, мы опустим. Нетрудно заметить, что пока значение уk мало, т. е. плоскость наблюдения находится в пределах объекта, изображение под данным углом в любой плоскости, параллельной xz, будет описываться выражением (4.27). Суть эффекта затенения заключается в том, что мы наблюдаем под некоторым углом сумму теней различных сечений.
Формула (4.27) представляет собой выражение для томографической проекции трехмерного объекта, представленного в виде набора плоскостей. Таким образом, эффект затенения приводит к тому, что мы наблюдаем не изображение объекта, восстановленного с голограммы, а его томографическую проекцию, полученную под углом φi, т. е. мы видим не сам объект, а его преобразование Радона. Очевидно, что нам хотелось бы наблюдать в плоскости xz само изображение томограммы, а при переходе от одной плоскости r другой — его изменение.
Вспомним методы восстановления продольных томограмм, которые анализировались в пункте 3.3 и подходят в данном случае лучше других. Согласно полученным нам соотношениям выражение для томограммы fi(x, z) можно представить в виде
![]() (4.28)
(4.28)
где N — число ракурсов зондирования; i — номер наблюдаемой томограммы; yi — расстояние от ее начала координат в области объекта; координату z, как и прежде, мы опускаем;
![]() (4.29)
(4.29)
— фильтрованная проекция;
![]()
— фильтрующая функция.
Найдем связь между фильтрованными проекциями f и изображением сечений f(x). Преобразуем уравнение следующим образом:
![]()
![]() (4.30)
(4.30)
Учитывая, что fj(p) есть преобразование Радона функции f(x,y), переписываем (4.30) в виде
![]()
![]() (4.31)
(4.31)
Используя соотношение h(ax) = h(x)/a2, преобразуем (4.31):
![]() (4.32)
(4.32)
Заметим, что наш объект по оси y представляет собой набор транспарантов. В этом случае с учетом обозначения (4.29) перепишем (5,32) в виде
![]() (4.33)
(4.33)
где f — фильтрованная томограмма.
Подставим полученное выражение для фильтрованной проекции в формулу (4.28), описывающую томограмму при yi=0:
![]() (4.34)
(4.34)
Для выделения сечения при произвольном yi, выражение (4.28) приводится к виду
![]()
![]() (4.35)
(4.35)
Таким образом, если у нас имеется набор томограмм fk и мы хотим синтезировать из них трехмерное изображение, причем в каждой плоскости наблюдать неискаженную томограмму fi, необходимо построить голографический дисплей, в котором выполняются преобразования волнового фронта, удовлетворяющие уравнению (4.35).
Рассмотрим последовательность операций, которые необходимо выполнить над исходным набором томограмм fk(x,z):
1. Фильтрация томограмм. Хранящийся в памяти ЭВМ массив с рассчитанными томограммами fk(x,z) надо преобразовать по формуле:
![]() (4.36)
(4.36)
где z — параметр.
2. Последовательная запись голограммы фильтрованных томограмм. Из (4.35) следует, что необходима многоракурсная подсветка транспарантов ![]() (N — число ракурсов). В каждом ракурсе интенсивность должна осуществляться по закону 1/cosφi. Для того чтобы на этапе восстановления каждая томограмма фокусировалась на расстоянии уk от плоскости голограммы, можно применять метод, предложенный в пункте 4.4.1.
(N — число ракурсов). В каждом ракурсе интенсивность должна осуществляться по закону 1/cosφi. Для того чтобы на этапе восстановления каждая томограмма фокусировалась на расстоянии уk от плоскости голограммы, можно применять метод, предложенный в пункте 4.4.1.
3. Восстановление голограммы. На данном этапе с каждого участка голограммы восстановятся все фильтрованные изображения томограмм, которые будут распространяться под углом φi. При восстановлении всей голограммы одновременно в пространстве изображений сформируется поле, определяемое выражением, (4.35), так как восстановятся все ракурсы (сумма по j) и все сечения (сумма по k).
В проделанных экспериментах трехмерный объект представлял собой наклонный столбик, у которого плотность почернения в поперечном горизонтальном сечении изменялась по гауссовскому закону. Трехмерный объект был задан пятью транспарантами из продольных сечений функции Гаусса плоскостью y=0, проходящей через центр гауссианы, и четырьмя крайними сечениями y=±Δ, ±2Δ. Транспаранты моделировались промежутками Δ =
Для иллюстрации эффектов затенения сечений в голографическом дисплее проводились эксперименты с аналогичными транспарантами, которые не подвергались ρ-фильтрации. Известно, что из них восстанавливаются суммарные изображения, наблюдаемые на плоском экране. При восстановлении изображений визуализирующий экран устанавливался на столике перпендикулярно направлению восстановления сечений, который мог перемещаться в этом направлении в любую сторону. Получаемые на экране изображения сечений трехмерного объекта регистрировались и вводились в ЭВМ для последующих измерений.
На рисунке 4.5a показаны денситомограммы сечений y=0; 3;
На рисунке 4.5б показаны денситомограммы тех же сечений, восстановленные с другой голограммы, зарегистрированной из нефильтрованных транспарантов. Изменение максимального значения сечений на рисунке 4.5а говорит об ослаблении эффекта затенения в отличие от денситомограмм на рисунке 4.5б, на которых все сечения имеют одну и ту же величину.
Таким образом, предварительное «искажение» томограммы [фильтрация (4.36)] на этапе записи позволяет на стадии восстановления избежать эффекта затенения и наблюдать неискаженную картину изображений сечений. Помещая в эту область экран, мы можем наблюдать и изображение томограмм, произвольно ориентированных в пространстве.
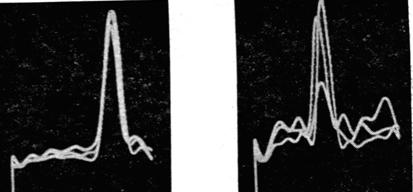
а) б)
а - при r-фильтрации транспарантов;
б – без фильтрации
Рисунок 4.5 – Денситограммы восстановленных изображений
Интересно отметить, что при визуальном наблюдении эффект затенения может остаться, хотя и ослабленный. Это объясняется тем, что угол наблюдения глаза мал и сумма по j (направлениям зондирования) в (4.35) будет вычисляться при малом числе слагаемых.
|
|