В настоящее время известно большое количество методов измерений, достаточно полно и достоверно описывающих исследуемые объекты и процессы. Однако возрастающие требования к ускорению научно-технического прогресса, повышению эффективности научных исследований приводят к необходимости разработки новых методов и средств измерений.
Проблема исследования внутренней структуры широкого класса объектов и процессов всегда выдвигалась как одна из основных в различных областях науки, техники и медицины. Она решалась методами интроскопии при диагностике изделий и спектроскопии при исследовании состава объектов. Как правило, результаты носили либо качественный характер (локализация дефектов), либо позволяли определять значение физической величины в малом объеме.
Значительный интерес представляют исследования пространственно-временных распределений (полей) физических величин внутри объектов. Как мы уже говорили, первым шагом на этом пути можно назвать метод диагностики, предложенный К. Рентгеном, который основан на зондировании объекта лучами, названными его именем, и регистрации прошедшего излучения. Он первый и обратил внимание на основной недостаток этого метода – образование суммарной картины изображений различных слоев объекта. Естественно, возникла задача получения изображения каждого изолированного слоя объекта — томограммы (от греческого tomos — слой). На протяжении 70 лет предпринимались различные попытки решения этой задачи. В медицинской диагностике наибольшую известность и распространение получила томография, которая была предложена Е. Бокажем в
Получение неискаженного изображения сечения объекта оказалось возможным лишь с появлением вычислительной томографии, которая представляет собой двухступенчатый метод исследований.
На первом этапе объект зондируется проникающим излучением с различных направлений, и прошедшее поле регистрируется, т. е. формируется набор проекций. На втором этапе вся совокупность полученной информации обрабатывается в каком-либо процессоре. Таким образом, томографические измерения являются косвенными — измеряемая величина связана с исследуемой некоторым функциональным отношением. Обработка усложняется еще и тем, что для восстановления томограммы необходимо решать обратную задачу. Очевидно, что это выдвигает высокие требования к системе обработки данных.
Математическим фундаментом томографии является интегральная геометрия, основы которой были заложены в работах И. Радона в
Задача восстановления изображений по их интегральным характеристикам носит гораздо более общий характер, чем диагностика внутренней структуры объектов, поэтому необходимость ее решения возникла в самых различных областях науки. Это привело к тому, что методы, которые сейчас объединены под общим названием томография, были независимо открыты и использовались целым рядом ученых, начиная с середины 50-х годов.
Так, в
Остановимся подробнее на понятии проекции изображения и методах ее получения. Широкое распространение томографии обусловлено еще и тем, что процесс получения проекций не представляет собой нечто искусственное и надуманное. Напротив, регистрация интегральной информации об объекте встречается на практике очень часто. Выделим три основных метода получения проекции.
Первый из них основан на зондировании объекта проникающим излучением и регистрации прошедшего излучения. Собственно этот метод сбора данных лежит в основе реконструктивной томографии. На рисунке 3.1 представлена схема получения проекций. Пусть нам необходимо определить распределение некоторой физической величины ![]() в сечении объекта. Тогда согласно схеме на используемое тело воздействует излучение, проникающее внутрь объекта. Оно взаимодействует с веществом, составляющим объект, и на выходе регистрируется излучение, прошедшее через тело. При этом, как правило, выдвигаются два предположения: во-первых, распространение излучения в исследуемой среде должно подчиняться лучевому уравнению, причем траектория луча L должна быть известна (обычно ее предполагают прямолинейной); во-вторых, взаимодействие излучения с веществом должно быть линейным. При соблюдении данных условий вдоль каждого луча в процессе распространения происходит накопление эффекта взаимодействия. Тогда величина излучения на выходе из объекта представляет собой интеграл вдоль траектории луча от искомого распределения физической величины в сечении объекта:
в сечении объекта. Тогда согласно схеме на используемое тело воздействует излучение, проникающее внутрь объекта. Оно взаимодействует с веществом, составляющим объект, и на выходе регистрируется излучение, прошедшее через тело. При этом, как правило, выдвигаются два предположения: во-первых, распространение излучения в исследуемой среде должно подчиняться лучевому уравнению, причем траектория луча L должна быть известна (обычно ее предполагают прямолинейной); во-вторых, взаимодействие излучения с веществом должно быть линейным. При соблюдении данных условий вдоль каждого луча в процессе распространения происходит накопление эффекта взаимодействия. Тогда величина излучения на выходе из объекта представляет собой интеграл вдоль траектории луча от искомого распределения физической величины в сечении объекта:
![]() (3.1)
(3.1)
Величину ![]() иногда называют луч-суммой. В тех случаях, когда траектория L—прямая линия, уравнение (3.1) представляет собой преобразование Радона функции
иногда называют луч-суммой. В тех случаях, когда траектория L—прямая линия, уравнение (3.1) представляет собой преобразование Радона функции ![]() .
.
Как правило, используется пучок, узкий вдоль оси ![]() ( рисунок 3.1,а), и в этом случае регистрируется прошедшее через объект излучение
( рисунок 3.1,а), и в этом случае регистрируется прошедшее через объект излучение ![]() , которое и называется проекцией. Регистрируемая функция
, которое и называется проекцией. Регистрируемая функция ![]() зависит от одной переменной, поэтому восстановить по одной проекции функцию двух переменных
зависит от одной переменной, поэтому восстановить по одной проекции функцию двух переменных ![]() невозможно. Для того, чтобы получить набор данных, достаточный для восстановления, применяют зондирование объекта с различных направлений. При этом (рисунок 3.1,б) мы можем получить интегральные характеристики функции
невозможно. Для того, чтобы получить набор данных, достаточный для восстановления, применяют зондирование объекта с различных направлений. При этом (рисунок 3.1,б) мы можем получить интегральные характеристики функции ![]() как некоторую двумерную функцию
как некоторую двумерную функцию ![]() . Основное достижение И. Радона состоит в том, что он доказал возможность восстановления функции
. Основное достижение И. Радона состоит в том, что он доказал возможность восстановления функции ![]() по ее интегралам по всем прямым
по ее интегралам по всем прямым ![]() и вывел формулу обращения.
и вывел формулу обращения.
 |
а) б)
а) - зондирование трехмерного объекта (1- источники; 2- детекторы; 3- объект);
б ) - сечение z - const
Рисунок 3.1. Схема получения проекций
Однако зондирование объекта проникающим излучением не единственный способ получения проекции функции ![]() . Другой способ связан с обработкой двумерных сигналов и изображений. Пусть нам дана некая функция
. Другой способ связан с обработкой двумерных сигналов и изображений. Пусть нам дана некая функция ![]() . Физически она может быть определена как изображение на экране монитора либо как некоторый самосветящийся объект (солнце, источники радио- и рентгеновского излучения в космосе и т. д.). Для того, чтобы получить проекции данной функции, будем последовательно закрывать отдельные участки изображения непрозрачным экраном (рисунок 3.2). Пусть в k-тый момент времени экран, край которого составляет с осью х угол
. Физически она может быть определена как изображение на экране монитора либо как некоторый самосветящийся объект (солнце, источники радио- и рентгеновского излучения в космосе и т. д.). Для того, чтобы получить проекции данной функции, будем последовательно закрывать отдельные участки изображения непрозрачным экраном (рисунок 3.2). Пусть в k-тый момент времени экран, край которого составляет с осью х угол![]() , оставляет открытой часть изображения Sk. Тогда детектор зарегистрирует часть излучения, определяемую выражением
, оставляет открытой часть изображения Sk. Тогда детектор зарегистрирует часть излучения, определяемую выражением
![]() (3.2)
(3.2)
Если мы передвинем экран в направлении n, перпендикулярном его краю L, на некоторую малую величину Δ, то детектор зарегистрирует другое значение
![]() (3.3)
(3.3)
 |
Рисунок 3.2. Схема получения проекции при движении экрана
Разность величин ![]() и
и ![]() будет равна интегралу от функции
будет равна интегралу от функции ![]() вдоль линии, толщина которой определяется различием положений экрана, т. е. величиной Δ. Фактически это соответствует луч-сумме функции
вдоль линии, толщина которой определяется различием положений экрана, т. е. величиной Δ. Фактически это соответствует луч-сумме функции ![]() вдоль прямой L. Последовательное движение экрана позволяет сформировать проекцию
вдоль прямой L. Последовательное движение экрана позволяет сформировать проекцию ![]() функции
функции ![]() под заданным углом
под заданным углом ![]() . Очевидно, что, изменяя направление движения непрозрачного экрана, нетрудно получить полный набор проекций исследуемой функции. На первый взгляд такой метод получения проекций носит несколько искусственный характер. Однако он нашел широкое применение в радио- и рентгеновской астрономии, где приборы, предназначенные для анализа изображений в соответствующем диапазоне длин волн имеют низкое разрешение.
. Очевидно, что, изменяя направление движения непрозрачного экрана, нетрудно получить полный набор проекций исследуемой функции. На первый взгляд такой метод получения проекций носит несколько искусственный характер. Однако он нашел широкое применение в радио- и рентгеновской астрономии, где приборы, предназначенные для анализа изображений в соответствующем диапазоне длин волн имеют низкое разрешение.
Третий метод получения проекций функции ![]() специфичен для оптического диапазона. На рисунке 3.3 приведена схема получения проекций изображения, представленного на экране. Цилиндрическая линза 3 фокусирует излучение, прошедшее через транспарант с изображением на регистратор в виде линейки детекторов. Нетрудно заметить, что линза фактически интегрирует падающее на нее излучение вдоль прямых, перпендикулярных образующим цилиндра, т. е. в фокальной области формируется проекция
специфичен для оптического диапазона. На рисунке 3.3 приведена схема получения проекций изображения, представленного на экране. Цилиндрическая линза 3 фокусирует излучение, прошедшее через транспарант с изображением на регистратор в виде линейки детекторов. Нетрудно заметить, что линза фактически интегрирует падающее на нее излучение вдоль прямых, перпендикулярных образующим цилиндра, т. е. в фокальной области формируется проекция ![]() . С помощью вращающейся вокруг оптической оси призмы Дове 2 нетрудно последовательно сформировать полный набор проекций функции
. С помощью вращающейся вокруг оптической оси призмы Дове 2 нетрудно последовательно сформировать полный набор проекций функции ![]() . Указанный метод получения интегральных характеристик применяется в настоящее время в системах обработки изображений [13].
. Указанный метод получения интегральных характеристик применяется в настоящее время в системах обработки изображений [13].
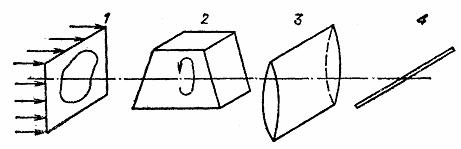 |
1 — транспарант с изображением,
2 — призма Дове;
3 — цилиндрическая линза;
4 — регистратор
Рисунок 3.3. Схема получения проекций оптических изображений
 |
а) б)
а—получение проекции; б—суммирование обратных проекций
Рисунок 3.4. Схема восстановления томограмм по алгоритму суммирования
обратных проекций
Ряд из них, имеющих существенное прикладное значение, но носящих специфический характер.
Как уже отмечалось, И. Радоном была получена формула, позволяющая определить по набору проекций ![]() саму функцию
саму функцию ![]() , т. е. решить обратную задачу. Однако работа И. Радона долгое время была известна только узкому кругу математиков, что привело к появлению целого ряда работ, в которых были предложены конструктивные алгоритмы восстановления, лишь косвенно связанные с формулой обращения. Это объясняется в первую очередь тем, что понятия интегральной геометрии носят очень наглядный характер и легко иллюстрируются простыми построениями.
, т. е. решить обратную задачу. Однако работа И. Радона долгое время была известна только узкому кругу математиков, что привело к появлению целого ряда работ, в которых были предложены конструктивные алгоритмы восстановления, лишь косвенно связанные с формулой обращения. Это объясняется в первую очередь тем, что понятия интегральной геометрии носят очень наглядный характер и легко иллюстрируются простыми построениями.
 |
а — ограниченное число проекций; б — бесконечное число проекций
Рис. 3.5. Суммарное изображение точки
Получившаяся функция ![]() носит название суммарного изображения. Из рисунка 3.5 видно, что функции
носит название суммарного изображения. Из рисунка 3.5 видно, что функции ![]() и
и ![]() имеют много общего. В частности, неоднородности, характеризующие
имеют много общего. В частности, неоднородности, характеризующие ![]() достаточно явно проявились на суммарном изображении. Существенным отличием является наличие артефактов вокруг каждой из неоднородностей. При увеличении числа проекций эти артефакты будут сливаться между собой. Нетрудно заметить, что каждая точка в суммарном изображении будет превращаться в многолучевую звезду (рисунок 3.5,а), а в пределе при бесконечном числе проекций превратится в функцию вида 1/r (рисунок. 3.5,б). Рассмотренный алгоритм был предложен Б. К. Вайнштейном для исследования
достаточно явно проявились на суммарном изображении. Существенным отличием является наличие артефактов вокруг каждой из неоднородностей. При увеличении числа проекций эти артефакты будут сливаться между собой. Нетрудно заметить, что каждая точка в суммарном изображении будет превращаться в многолучевую звезду (рисунок 3.5,а), а в пределе при бесконечном числе проекций превратится в функцию вида 1/r (рисунок. 3.5,б). Рассмотренный алгоритм был предложен Б. К. Вайнштейном для исследования
 |
 |
в)
а — получение проекции;
б — фурье-спектр проекции;
в — фурье-спектр томограммы
Рисунок 3.6. Схема восстановления томограмм по алгоритму фурье синтеза:
Простой и наглядный алгоритм основан на связи фурье-преобразований функций ![]() и
и ![]() . Представим функцию
. Представим функцию ![]() в виде набора синусоид, произвольно ориентированных в пространстве и постоянных вдоль одной из осей. На рисунке 3.6,а приведена одна из них. Рассмотрим проекцию синусоиды, полученную таким образом, что направление зондирования совпадает с образующей синусоиды. Нетрудно заметить, что она также будет представлять собой синусоиду, период которой совпадает с периодом исходной функции. Если направление зондирования не совпадает с образующей синусоиды, интеграл от нее вдоль любой прямой будет равен нулю. Таким образом, в фурье-спектр проекции, полученной под углом
в виде набора синусоид, произвольно ориентированных в пространстве и постоянных вдоль одной из осей. На рисунке 3.6,а приведена одна из них. Рассмотрим проекцию синусоиды, полученную таким образом, что направление зондирования совпадает с образующей синусоиды. Нетрудно заметить, что она также будет представлять собой синусоиду, период которой совпадает с периодом исходной функции. Если направление зондирования не совпадает с образующей синусоиды, интеграл от нее вдоль любой прямой будет равен нулю. Таким образом, в фурье-спектр проекции, полученной под углом ![]() , внесут вклад только те пространственные частоты функции
, внесут вклад только те пространственные частоты функции ![]() , образующие которых параллельны направлению зондирования. Если мы рассмотрим преобразование фурье-проекции
, образующие которых параллельны направлению зондирования. Если мы рассмотрим преобразование фурье-проекции ![]() , то увидим, что оно совпадает с распределением фурье-образа
, то увидим, что оно совпадает с распределением фурье-образа ![]() двумерной функции
двумерной функции ![]() вдоль линии, проходящей через начало координат и перпендикулярной направлению зондирования (рисунок 3.6,б).
вдоль линии, проходящей через начало координат и перпендикулярной направлению зондирования (рисунок 3.6,б).
Нетрудно заметить, что фурье-образы всех проекций позволяют определить в частотной плоскости значения всех компонент спектра пространственных частот функции ![]() (рисунок 3.6,в).
(рисунок 3.6,в).
 |
Рисунок 3.7 - Двумерный ![]() -фильтр
-фильтр
Мы рассмотрели два алгоритма, которые на основании простейших геометрических построений позволяют понять, каким образом можно из интегральных характеристик изображений-проекций восстановить искомую функцию. Связь этих алгоритмов с формулой обращения Радона и их математическое обоснование будут приведены в первой главе, здесь, во введении, мы хотели лишь подчеркнуть, что основы томографии достаточно очевидны и просты для понимания.
Успехи томографии как метода исследований внутренней структуры объектов привлекли внимание ученых к возможности использования интегральной геометрии для решения целого ряда практических задач, не связанных с диагностикой скрытых структур. Не случайно в целом ряде книг, посвященных томографии, делается упор на восстановление функций по их интегральным характеристикам (проекциям) независимо от способа получения последних, т. е. томография понимается как метод отображения и обработки информации.
Рассматривая томографию как новый метод переработки, преобразования и отображения многомерных сигналов и изображений, можно выделить несколько направлений, которые описываются в следующих параграфах.
Под данным направлением понимается совокупность методов и средств, позволяющих производить восстановление изображений по их проекциям, полученным различными способами. Такое восстановление необходимо, когда информация о каком-либо изображении представлена в виде интеграла. Подобная ситуация возникает в радио- и рентгеновской астрономии при сканировании неба линейными приемниками, в радиолокационных системах (РЛС) бокового обзора, сейсморазведке, хронотографии.
Преобразование Радона трансформирует изображение в одномерный сигнал определенного вида, что позволяет вычислять свертку и корреляцию двух изображений, линейную и нелинейную фильтрации, сжатие и кодирование информации в устройствах, предназначенных для обработки одномерных сигналов. Оценки показывают, что использование современных элементов оптоэлектроники (устройств, использующих поверхностные акустические волны, акустических модуляторов и т. д.) позволяет таким системам обработки изображений успешно конкурировать с другими, аналогичными по назначению устройствами.
В данном направлении, прежде всего, представляет интерес определение формы поверхности по набору ее многоракурсных изображений, при котором используются методы томографии. Актуальны также задачи построения дисплея, позволяющего формировать трехмерные изображения из набора сечений, причем таким образом, чтобы избежать эффекта затенения одних сечений другими. Интересным является направление, связанное с сочетанием голографических и томографических принципов для трехмерного отображения скрытых структур.
Данное направление — наиболее распространенная область применения томографической обработки информации. В настоящее время известны томографические системы для широкого класса измеряемых распределений физических величин внутри объектов при самых различных видах воздействия на них.
Определение и исследование внутренней структуры различных объектов и процессов — задача, в которой органично сочетаются интересы науки, техники и медицины. Не случайно за последние 10 лет томография нашла применение в самых разных областях естествознания: в астрономии — для получения изображений распределенных источников в рентгеновском и радиодиапазонах; в науках о Земле — для трехмерного картирования мантии Земли и определения крупномасштабных явлений в океане, в физике — для измерения распределений физических величин; в биологии и медицине — для диагностики биологических объектов и человека; в химии и кристаллографии — для получения изображений молекул; в информатике — для обработки многомерных сигналов; в машино- и приборостроении — для неразрушающего контроля объектов от многотонных конструкций до изделий микроэлектроники.
Для воздействия на объекты с целью последующего восстановления исследуемых характеристик используют физические процессы произвольной природы. Наибольшее применение в настоящее время нашли рентгеновские и гамма-лучи, тяжелые частицы (альфа-частицы, протоны), электронные пучки, магнитные поля (ядерная магниторезонансная (ЯМР) томография), ультразвук, сейсмические и акустические волны и т д. Широкий класс объектов и процессов может быть исследован воздействием на них оптического излучения. Наличие большого числа систем, с одной стороны, отличающихся друг от друга, а с другой — использующих одни и те же принципы, привело к необходимости некоторой их дифференциации. В литературе рассматривались различные принципы классификации методов данного направления, которые, как правило, сводились к разделению их по виду воздействия на исследуемый объект. По аналогичному принципу построены различные обзоры, посвященные применению томографических методов. Согласно этому признаку различают рентгеновскую, акустическую, оптическую и прочую томографию.
Основным недостатком такой классификации является то, что разделенные по указанному принципу томографические измерения зачастую используют одни и те же физические законы и математический аппарат для описания процесса распространения зондирующего либо эмиссионного излучения в объекте. Архитектура томографических систем, алгоритмическое программное обеспечение в данном случае во многом совпадают, а отличие касается лишь устройств зондирования и регистрации. Для специалистов, занимающихся разработкой новых томографических методов, разделение систем по виду воздействия приводит к тому, что усложняется проникновение идей из одной области томографии в другую.
Более продуктивной, на наш взгляд, была бы классификация, построенная на других принципах. Рассмотрим процесс построения томографической системы, предназначенной для тех или иных физических измерений. Как правило, он начинается с анализа процесса распространения излучения в веществе. Из определенных физических посылок выбирается уравнение, описывающее связь между измеряемыми параметрами внутри объекта и характеристиками излучения (поля). Важно отметить, что для многих внешне отличных областей исследования уравнение распространения оказывается одинаковым. Так, например, закон Бугера-Ламберта-Бэра описывает связь между показателем поглощения и зондируемым полем практически для всех диапазонов электромагнитного излучения. Волновое уравнение позволяет определить связь между внутренней структурой объекта и прошедшим полем в акустическом, оптическом и других диапазонах. Уравнение распространения, в свою очередь, позволяет получить уравнение связи между исследуемой величиной и измеряемой характеристикой поля.
В таблице 3.1 приведены некоторые виды уравнений распространении и связи. Основным достоинством такой классификации является то, что она позволяет сразу определить наличие и вид формулы обращения независимо от того, в какой области применения томографии она была получена. Это способствует взаимному проникновению идей обработки и методов решения обратных задач, которые часто развиваются независимо в самых различных областях науки.
Наиболее ярким примером такого плодотворного обмена идеями может служить дифракционная томография. Заводившаяся в работах Е. Вольфа для решения оптической задачи восстановления потенциала рассеяния по голографическим измерениям, она затем обрела новую жизнь в акустических приложениях, а сейчас вновь с успехом применяется в оптических измерениях.
Таблица 3.1 – Классификаия методов томографии
| Уравнение |
Исследуемая величина |
Измеряемая величина |
Уравнение |
Формула обращения |
Основные области |
| Уравнение переноса излучения (закон Бугера) |
Показатель поглощения |
Интенсивность поля |
Преобразование Радона |
Есть |
Абсобционная томография в различных диапазонах |
| Уравнение эйконала для слабой рефракции (прямолинейные лучи) |
Показатель преломления |
Фаза поля |
То же |
>> |
Томография фазовых объектов (УЗВ-диагностика, оптика) |
| Уравнение эйконала для сильной рефракции (криволинейные лучи) |
То же |
То же |
В общем виде нет |
Есть для геодезических кривых |
Рефракционная томография (сейсморазведка, акустика, оптика) |
| Волновое уравнение (борновское приближение) |
Диэлектрическая проницаемость |
Комплексная амплитуда поля |
Уравнение рассеянного поля |
Есть |
Дифракционная томография (акустика, оптика) |
| Уравнение переноса излучения для различных сред |
Коэффициент экстинкции |
Интенсивность поля |
Модифицированное преобразование Радона |
Есть для частных случаев |
Эмиссионная томография (частицы, оптика) |
| Уравнение Блоха |
Распределение ядерных спинов |
Релаксация ВЧ-поля |
Преобразование Радона |
Есть |
ЯМР-томография |
Таблица, иллюстрирующая предложенную классификацию, не претендует на законченность. Напротив, привлечение для томографического исследования новых физических методов (электронного парамагнитного резонанса, атомно-спектральных и т. д.) будет непрерывно дополнять и расширять таблицу. Будем надеяться, что она поможет в поиске формулы обращения и в дальнейшем при выборе алгоритма решения обратной задачи.
Следующим шагом в процессе построения томографической системы является ее информационный анализ Недостаточно установить уравнение связи и наличие возможности решения обратной задачи, так как алгоритм существенно зависит от того количества информации, которое можно зарегистрировать в процессе исследования.
В основе математического аппарата томографии лежит интегральная геометрия, и в первую очередь преобразование Радона. При анализе оптических томографов мы будем широко использовать свойства этого преобразования. В настоящем параграфе рассмотрим основные математические понятия интегральной геометрии: определение и свойства преобразования Радона. Мы будем: следовать посвященным подробному анализу перечисленных вопросов. При этом будем стараться, может быть в ущерб математической строгости, не выходить за рамки институтского курса математического анализа.
Свойства преобразования Радона и формулы его обращения целесообразно рассматривать не только для двумерного случая, но и для функций трех переменных, так как в последнее время появились работы, в которых исследуются функции, зависящие от большого числа параметров.
Пусть дана функция f(x, y), которая определена в некоторой области D. Рассмотрим некоторую прямую L на плоскости ху, пересекающую область D. Тогда, интегрируя функцию f{x,y) вдоль линии L, получаем проекцию или линейный интеграл функции f. Интегрирование вдоль всех возможных линий L на плоскости позволяет определить преобразование Радона
![]() (3.4)
(3.4)
где ds — приращение длины вдоль прямой L.
 |
Рисунок 3.8 – К определению преобразования Радона
Преобразование Радона может быть представлено в другом виде. Запишем нормальное уравнение прямой L:
![]() (3.5)
(3.5)
где p — расстояние от начала координат до прямой (рисунок 3.8), j — угол между р и х. Используя выражения
![]()
нетрудно записать
![]() (3.6)
(3.6)
Если функция f равна нулю вне области D, то пределы интегрирования в (3.6) могут быть конечны.
Используя векторную запись прямой на плоскости, формулу (3.2) можно представить в виде
![]() (3.7)
(3.7)
где ![]() — единичный вектор вдоль оси
— единичный вектор вдоль оси ![]() — скалярное произведение двух векторов.
— скалярное произведение двух векторов.
Тогда преобразование Радона может быть записано с использованием d-функций, для выделенной прямой ![]() :
:
![]() (3.8)
(3.8)
или с учетом (3.7):
![]() (3.9)
(3.9)
При фиксированном угле j проекция f(p,j) изменяется по р в направлении, определенном вектором x. В тех случаях, когда функция f(p,j) известна только для некоторых значений р, j можно говорить о выборке из преобразования Радона или луч-сумме.
Если задана функция трех переменных f(x,y,z), тогда, используя векторную запись ![]() и единичный вектор x, можно записать уравнение плоскости интегрирования функции f:
и единичный вектор x, можно записать уравнение плоскости интегрирования функции f:
![]()
Преобразование Радона будет иметь следующий вид:
![]() (3.10)
(3.10)
где р — расстояние от начала координат до плоскости интегрирования; x — единичный вектор вдоль р, который определяет ориентацию плоскости.
Хотя выражение (3.10), мало отличается от двумерного преобразования Радона, представленного формулой (3.8), необходимо помнить, что в (3.9) интегрирование ведется по плоскостям, а не по прямым (Здесь и далее, если не указаны пределы интегрирования, то оно ведется по бесконечным пределам.) Очевидно, что для полного задания преобразования Радона необходимо знание f для всех p и x.
Рассмотрим два примера преобразований Радона конкретных функций.
1. Пусть
![]()
тогда
![]()
Использовав ортогональное линейное преобразование
 ,
,
приведем f к виду
![]()
тогда
![]()
2. Рассмотрим преобразование двумерной rect-функции, определенной формулой
![]()
Из соображений симметрии ясно, что проекции можно рассматривать только в области изменения углов ![]() . Нетрудно заметить, что можно выделить три различные области определения проекций при фиксированном φ (рисунок 3.9, прямые 1, 2 и 3). Вычисляя длину отрезка прямой внутри области задания функции f(x, у), можно получить значения преобразования Радона:
. Нетрудно заметить, что можно выделить три различные области определения проекций при фиксированном φ (рисунок 3.9, прямые 1, 2 и 3). Вычисляя длину отрезка прямой внутри области задания функции f(x, у), можно получить значения преобразования Радона:

Для определения свойств преобразования Радона используем формулу (3.8) как наиболее удобную.

Рисунок 3.9 Преобразование Радона двумерной rect-функции
1. Преобразование f(p, ξ) есть однородная функция со степенью однородности 1, т. е.
![]() (3.11)
(3.11)
для ![]() .
.
Нетрудно заметить, что при ![]()
![]() , (3.12)
, (3.12)
т.е. преобразование Радона есть четная функция.
Из выражения (3.8) следует, что при фиксированном р, меняя значения ξ, можно полностью определить преобразования Радона функции f(x). Действительно, полагая ![]() ,
, ![]() , можно записать
, можно записать
![]()
2. Пусть даны две функции f1 и f2 с константами α1 и α2, тогда
![]() (3.13)
(3.13)
Таким образом, преобразование Радона линейно для любых функций f1 и f2 и любых чисел α1 и α2.
3. Пусть дано некоторое, линейное преобразование переменных x1, x2, ..., xn, такое, что Ах=у или
![]() .
.
Тогда преобразование Радона функции ![]() можно представить в виде
можно представить в виде
![]()
![]() (3.14)
(3.14)
где ![]() , А-1 – линейное преобразование, сопряженное преобразованию А. Это свойство целесообразно проиллюстрировать примером.
, А-1 – линейное преобразование, сопряженное преобразованию А. Это свойство целесообразно проиллюстрировать примером.
Пусть надо найти преобразование Радона функции  . Тогда исходной функцией является
. Тогда исходной функцией является ![]() , а преобразование координат имеет вид
, а преобразование координат имеет вид
![]()
Сопряженное преобразование единичного вектора ξ есть неединичный вектор ![]() ,
, ![]() Используя (3.13), после нормировки на
Используя (3.13), после нормировки на ![]() можно записать
можно записать

4. Если дана функция ![]() , то нетрудно определить ее преобразование Радона:
, то нетрудно определить ее преобразование Радона:
![]() (3.15)
(3.15)
Приведем пример:
![]() , где
, где ![]() .
.
Из выражения (3.15) и примера видно, что смещение функции в пространственной области приводит к сдвигу проекций вдоль р, причем величина сдвига зависит от угла зондирования φ.
5. Преобразование Радона от производной функции ![]() можно определить из выражения
можно определить из выражения
 , где
, где ![]()
В общем случае это свойство можно записать в виде
 (3.16)
(3.16)
Из данного свойства следует, что

или в более общем виде
![]() , (3.17)
, (3.17)
где ![]() -- однородный многочлен степени k с постоянными коэффициентами.
-- однородный многочлен степени k с постоянными коэффициентами.
6. Производную преобразования Радона f(p, ξ) по одной из компонент ξk можно представить в виде
![]() (3.18)
(3.18)
Используя следующее свойство δ-функции:
![]()
(3.16) можно переписать в виде
![]()
или
![]() (3.19)
(3.19)
Одним из важнейших свойств преобразования Радона является его связь с преобразованием Фурье. Введем следующие обозначения для n-мерного преобразования Фурье функции ![]() :
:
![]() (3.20)
(3.20)
где ![]() — координаты в частотной плоскости;
— координаты в частотной плоскости; ![]() — оператор n-мерного преобразования Фурье.
— оператор n-мерного преобразования Фурье.
Обратное преобразование Фурье представим в виде
![]() (3.21)
(3.21)
Для того, чтобы выявить связь между преобразованиями Радона и Фурье, запишем (3.19) в следующем виде:
![]() где t – действительная переменная. Тогда, введя обозначения
где t – действительная переменная. Тогда, введя обозначения ![]() и
и ![]() , нетрудно получить
, нетрудно получить
![]()
или с учетом (3.11)
![]() (3.22)
(3.22)
Из (3.21) следует фундаментальная связь между n-мерным преобразованием Фурье и преобразованием Радона: для того, чтобы осуществить n-мерное преобразование Фурье функции, необходимо сначала выполнить ее преобразование Радона, а затем осуществить одномерное преобразование Фурье проекции по ее радиальной переменной.
В операторном виде это записывается достаточно просто:
![]()
Однако, учитывая линейность, данное преобразование можно представить в виде:
![]() ,
,
т.е. для того чтобы вычислить преобразование Радона функции можно определить ее n-мерный фурье-образ и взять обратное одномерное преобразование Фурье по одной координате. Особенно это удобно для анализа двумерных функций, где существуют многочисленные таблицы преобразований Фурье от различных функций.
Рассмотрим следующий пример. Пусть дана функция
![]()
Ее двумерный фурье-образ известен и равен
![]()
Введем новые координаты ![]() , где
, где ![]() , тогда
, тогда
![]()
а его одномерное обратное фурье-преобразование равно преобразованию Радона от функции ![]() :
:

Последний интеграл известен, поэтому окончательно можно записать следующее:
![]()
В дальнейшем мы в основном будем анализировать преобразование Радона двумерных функций. В этом случае из (3.21) можно определить следующую связь между фурье-образом проекций и спектром функции ![]() :
:
![]()
![]() (3.23)
(3.23)
Из (3.20) следует, что фурье-образ проекции представляет собой спектр функции f(x,y) вдоль прямой ![]() , проходящей через начало координат в частотной плоскости под углом
, проходящей через начало координат в частотной плоскости под углом ![]() . Он является одномерным центральным сечением двумерного фурье-образа функции f.
. Он является одномерным центральным сечением двумерного фурье-образа функции f.
В литературе это свойство называют теоремой о центральном слое или центральном сечений.
Решение задачи восстановления функций из ее интегралов по гиперплоскостям было впервые получено Радоном. При этом была доказано, что формулы, выражающие функцию f(x), различны для пространств четной и нечетной размерности. Мы приведём различные представления указанных формул без доказательств и ограничимся лишь случаем двух и трех переменных.
Преобразование Радона имеет формулу обращения, которая для двумерной функции f(x) представляется в виде
![]() (3.24)
(3.24)
где Г — произвольный контур в пространстве ξ, охватывающий точку ![]() .
.
Знак ∫ означает, что интеграл берется в смысле главного (регуляризованного) значения. Перепишем (3.23) следующим образом:
![]() (3.25)
(3.25)
Выбирая контур Г в виде окружности единичного радиуса, получаем
![]()
![]()
Тогда
 (3.26)
(3.26)
или в смысле регуляризованного значения
 (3.27)
(3.27)
Выражение (3.25), (3.26) представляют собой запись решения интегрального уравнения Радона.
Возможно также и другое представление формулы (3.27):
 (3.28)
(3.28)
Формулу (3.28) можно записать в виде

где ![]() -- оператор преобразования Гильберта, равный внутреннему интегралу формулы (3.27).
-- оператор преобразования Гильберта, равный внутреннему интегралу формулы (3.27).
Эквивалентной записью является и следующее представление (3.27):

 (3.29)
(3.29)
Формула обращения для функции трех переменных f(x) определяется выражением:
![]() (3.30)
(3.30)
Здесь интегрирование ведется по сфере единичного радиуса с центром в начале координат; Δ — оператор Лапласа.
Выражение (3.29) может быть представлено в виде
![]()
при этом единичный вектор ![]() и
и ![]() определяется выражениями
определяется выражениями
![]() ,
,
где q — полярный, а j — азимутальный углы.
Анализ и сопоставление формул обращения для двумерного и трехмерного случаев позволяют увидеть их основное отличие.
Для трехмерного случая формула обращения локальна, т. е. для определения значения функции f в точке х необходимо знать интегралы по плоскостям, проходящим через точку х, и по бесконечно близким плоскостям. Это следует непосредственно из формулы (3.30), так как для вычисления по ней функции f необходимо двукратно продифференцировать все проекции и суммировать значения производных в точке х.
В двумерном случае, как следует из (3.28), для определения значения f в точке х необходимо знать интегралы по всем прямым, так как для вычисления внутреннего интеграла по р требуется задание проекции для всех р.
Это существенное отличие и определяет алгоритмы вычисления функций f(x) по их проекциям.
Рассмотрим методы восстановления томограмм двумерных объектов, описываемых функцией f(x,y) по их одномерным параллельным проекциям.
В этом случае направление проецирования определяется одним параметром – углом между осями p и x.
В настоящем параграфе рассмотрим алгоритмы, основанные на
интегральных преобразованиях, и определим набор тех операций над проекциями, которые необходимы для восстановления томограмм. Реализация указанного класса алгоритмов в оптических системах наиболее перспективна, так как одно из основных достоинств оптических процессоров — простота выполнения интегральных преобразований.
Формула обращения Радона (3.24) может быть преобразована к виду :
![]()
 (3.31)
(3.31)
![]() Для ее вычисления необходима следующая последовательность
Для ее вычисления необходима следующая последовательность
операций:
1) в одном канале каждая проекция «сглаживается», т. е. выполняется операция одномерной свертки ![]() с функцией
с функцией ![]() . В другом канале проекции остаются без изменения. Далее все операции над проекциями одинаковы в обоих каналах;
. В другом канале проекции остаются без изменения. Далее все операции над проекциями одинаковы в обоих каналах;
2) каждая проекция поворачивается в плоскости ху на соответствующий
угол j;
3) все повернутые проекции «растягиваются» в направлении, перпендикулярном оси р, т. е. реализуется переход от одномерной функции к двумерной![]() . Эта операция носит название обратного проецирования;
. Эта операция носит название обратного проецирования;
4) в обоих каналах преобразованные проекции суммируются (интегрируются по j);
5) вычисляется разность изображений, полученных в каждом из каналов.
Достоинством данного алгоритма можно назвать то, что на всех этапах вычисления томограммы преобразуемые функции положительные, и поэтому первые четыре операции могут быть выполнены как в когерентной, так и в некогерентной оптической системе. Недостатком данного алгоритма является двухканальность обработки проекций.
Выполним одномерное преобразование Фурье над обеими частями уравнения (3.9):
![]() (3.32)
(3.32)
В (3.31) фурье-сопряженная к р частотная координата ρ может изменяться в пределах (—∞, + ∞), а переменная φ является параметром, который может принимать любые значения из диапазона углов [0, π) или (–π /2, + π/2). Этот факт отражен в (3.32) путем записи переменных ρ и φ через точку с запятой. В полярной системе координат ρ, φ правую часть (3.32) можно записать в виде двумерного преобразования Фурье F (ρ, φ). Спектры проекций также можно записать в полярной системе координат в виде следующей функции:
 (3.33)
(3.33)
Тогда выражение (1.29) будет соответствовать теореме о центральном слое: ![]() ( 3.34)
( 3.34)
где F – фурье-образ f.
Отсюда следует, что искомая томограмма f(x,y) получается простым обратным преобразованием Фурье выражения ( 3.34):
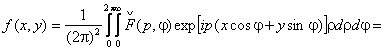
 ( 3.35)
( 3.35)
Таким образом, в методе фурье-синтеза вначале формируется двумерный спектр томограммы из одномерных фурье-образов проекций по полярной сетке отсчетов, а затем выполняется обратное двумерное преобразование Фурье также в полярной системе координат.
При численной реализации метода фурье-синтеза используют алгоритмы быстрого преобразования Фурье (БПФ). Для этой цели необходима промежуточная операция интерполяции значения спектров проекций с полярной сетки отсчетов на прямоугольную.
Возможна также следующая модификация метода фурье-синтеза. Из выражений ( 3.32), ( 3.34) следует, что значения одномерного фурье-образа любой ψ-й проекции совпадают со значенияш двумерного фурье-спектра искомой томограммы вдоль прямой ρ sin (φ – ψ) = 0, проходящей через начало координат частотной плоскости ρφ под углом ψ к базовой линии. Если все спектры проекций в частотной плоскости ρφ повернуть на соответствующий угол и накопить, т. е. просуммировать, то в результате сформируется двумерный спектр
 ( 3.36)
( 3.36)
Для вычисления интеграла применим следующее свойство δ-функций :
![]()
Тогда
 ( 3.37)
( 3.37)
Из теоремы о центральном слое ( 3.34) следует, что
![]() ( 3.38)
( 3.38)
Поэтому искомую томограмму можно восстановить из произведения ρS(ρ, φ) двумерным обратным преобразованием Фурье:
 ( 3.39)
( 3.39)
Для восстановления томограммы по формуле ( 3.39) необходима выполнить следующие операции: 1) вычислить фурье-образы проекций ![]() ; 2) повернуть полученный одномерный спектр в частотной плоскости ρφ под углом ψ. В двумерной плоскости такой одномерный фурье-спектр можно описать функцией
; 2) повернуть полученный одномерный спектр в частотной плоскости ρφ под углом ψ. В двумерной плоскости такой одномерный фурье-спектр можно описать функцией ![]() ; 3) накопить все спектры в плоскости ρφ. Результат накопления описывается функцией
; 3) накопить все спектры в плоскости ρφ. Результат накопления описывается функцией ![]() ; 4) умножить полученный спектр
; 4) умножить полученный спектр ![]() на двумерный фильтр ρ; 5) выполнить двумерное обратное преобразование Фурье.
на двумерный фильтр ρ; 5) выполнить двумерное обратное преобразование Фурье.
После выполнения первых трех операций в фурье-плоскости одномерные спектры будут расположены в виде некоторой радиальной структуры-звезды (рисунок 3.6в). Поэтому плотность отсчетов в двумерном спектре по координате ρ обратно пропорциональна ρ. Это видно также из выражения (3.37). Отсюда становится ясным физический смысл четвертой операции. Она выравнивает интегральную плотность отсчетов в спектре по всей частотной плоскости.
Подставим в (3.35) выражение ( 3.32) для фурье-образа проекции, поменяв порядок интегрирования по p и r, получим:
 ( 3.40)
( 3.40)
Введем функцию:
![]() ( 3.41)
( 3.41)
Тогда ( 3.37) примет вид
 ( 3.42)
( 3.42)
где ![]() ( 3.43)
( 3.43)
– фильтрованная проекция.
Фильтрующая функция h(p) может быть записана в виде обобщенной функции Р[1/р2], т.е.
H(p) = –(1/2π2)P[1/p2] ( 3.44)
На рисунке 3.10 схематично изображена фильтрующая функция h(р) и ее частотный фильтр |r|. Видно, что, подставив данную функции в ( 3.43), из ( 3.42) получим формулу инверсного преобразований Радона (3.26).
Для восстановления томограмм по формуле (3.42) необходимы следующие операции: 1) одномерная фильтрация каждой проекции (3.43) фильтрами (3.41), (3.44), называемая r-фильтрацией проекций; 2) поворот проекций в плоскости ху на соответствующий угол φ; 3) замена координаты р на x соs φ + у sin φ. Эта операция называется обратным проецированием, так как она в некотором смысле обратна операции получения проекций, т. е. операции прямого проецирования. Каждая одномерная проекция при этом как бы «растягивается» в направлении, перпендикулярном оси p, т.е. становится двумерной функцией ![]() ; 4) суммирование всех фильтрованных обратных проекций.
; 4) суммирование всех фильтрованных обратных проекций.
 |
а) б)
Рисунок 3.10 - Фильтрующая функция (а) и ее одномерный r-фильтр (б)
Отметим особенность данного алгоритма, которая может оказаться существенной при его реализации в оптической системе. Суть ее заключается в том, что при фильтрации проекции фильтром (3.41) значение спектра на нулевых частотах становятся равными нулю, т.е. при ![]() . Но с другой стороны,
. Но с другой стороны,
![]() .
.
Следовательно, фильтрованные проекции ![]() должны быть биполярными. Поэтому при их суммировании отрицательные участки одних фильтрованных обратных проекций компенсируются положительными значениями обратных проекций, что приводит в конечном счете к восстановлению самой томограммы.
должны быть биполярными. Поэтому при их суммировании отрицательные участки одних фильтрованных обратных проекций компенсируются положительными значениями обратных проекций, что приводит в конечном счете к восстановлению самой томограммы.
Возможен также другой подход к решению задачи восстановления томограммы.
Применив к обеим частям выражения ( 3.34) обратное преобразование Фурье, получим : 
поэтому ее называют суммарным или интегральным изображением. Учитывая выражение ( 3.35) и
![]()
можно получить следующую связь суммарного изображения с исходной функцией:
![]() , где
, где ![]() - значок двумерной свертки.
- значок двумерной свертки.
Таким образом, суммарное изображение S(x,y) представляет собой низкочастотный вариант томограммы, так как фильтр ![]()
![]() ослабляет ее высокие пространственные частоты. Это приводит к «размытию» мелких деталей на суммарном изображении.
ослабляет ее высокие пространственные частоты. Это приводит к «размытию» мелких деталей на суммарном изображении.
Как следует из ( 3.34), для устранения этого размытия спектр суммарного изображения S(x,y) необходимо умножить на двуменый r-фильтр. Восстанавливающее действие этого фильтра основ, но на усилении высоких пространственных частот суммарно изображения, что приводит к подчеркиванию его мелких деталей.
В пространственной области алгоритму ( 3.34) соответствует выражение
![]() ,
,
так как обратное двумерное преобразование Фурье от ρ имеет вид обобщенной функции
![]()
В заключение отметим, что процесс восстановления томограмм является линейным. Этот факт можно использовать для анализа алгоритмов восстановления томограммы следующим образом.
Предположим, что исследуемый объект описывается двумерной d-функцией, поэтому фильтрованная проекция ( 3.44) совпадав с самим фильтром h(r). Следовательно, томограммой такого объекта будет суммарное изображение ( 3.42) из обратных проекций фильтра
 ( 3.46)
( 3.46)
Исходя из линейности процесса синтеза томограмм, можно сделать
вывод, что томограмма объекта f(х,y), восстановленная с помощью фильтра h, связана с исходной функцией f(х,у) соотношением свертки с g(х,у), т. е.
![]() ( 3.47)
( 3.47)
Подставляя в ( 3.46) h(r) =d(r), получаем

Этот результат совпадает с ранее полученным выражением ( 3.46) связывающим суммарное изображение объекта с самим объектом. Таким образом, функцию g можно считать импульсным откликом процесса восстановления томограмм. По ее виду, полуширине и т. п. можно судить о качестве восстановления.
До настоящего раздела рассматривались методы восстановления, двумерных томограмм по одномерным проекциям. Задача исследования внутренней структуры трехмерного объекта сводилась к решению ряда задач восстановления двумерных томограмм набора параллельных слоев объекта.
При этом предполагалось, что все оси зондирующих пучков излучения лежат в одной плоскости, например xy и пересекаются в одной точке О.
В зависимости от ориентации восстанавливаемых сечений различают два вида томограмм: а) поперечные томограммы — изображения сечений объекта, параллельных плоскости осей зондирующих пучков; б) продольные томограммы – изображение сечений объекта, перпендикулярных плоскости осей зондирующих пучков.
 |
1- плоскость
2- кононическая поверхность
Рисунок 3.11 -Различные варианты схем зондирования или наблюдения трехмерного объекта
Описанные схемы зондирования распространены в методах классической томографии с перемещением пары источник – регистратор по различным траекториям. К данным схемам, как будет показано далее, можно отнести также методы кодированного источника, томосинтеза, эктомографии. При исследовании трудно доступных объектов, например плазмы, оси зондирующих пучков занимают выборочные дискретные положения из приведенных выше фигур. Поэтому в ряде работ стали исследовать методы восстановления томограмм трехмерных объектов по их двумерным параллельным проекциям. К данной проблеме можно также отнести задачу восстановления трехмерной внутренней структуры объектов по их двумерным коническим проекциям.
В настоящем параграфе рассмотрим новый методический подход к задаче восстановления трехмерных томограмм по двумерным проекциям, полученным при различных схемах проецирования. Предлагаемый подход по мнению авторов более простой и наглядный.
Все дальнейшие рассуждения основаны на теореме о центральном слое для двумерных проекций. Для ее вывода воспользуемся записью двумерных проекций в виде
![]() (3.48)
(3.48)
 |
а – пространственная область;
б – частотная область
Рисунок 3.12 – Схема проецирования трехмерного объекта
Применим двумерное преобразование Фурье к обеим частям уравнения (3.45):
![]() (3.49)
(3.49)
С другой стороны трехмерный фурье-спектр функции f в цилиндрических координатах R, z можно записать в виде
![]() (3.50)
(3.50)
где ![]() -- частотные координаты; k – единичный вектор, направленный вдоль оси z.
-- частотные координаты; k – единичный вектор, направленный вдоль оси z.
Заменяя в этой записи переменные интегрирования R, z на p, t и сравнивая выражения (3.46) и (3.47), получаем теорему о центральном слое
![]() (3.51)
(3.51)
В данном соотношении уравнение (ω, τ)=0 описывает плоскость, проходящую через начало координат частотного пространства перпендикулярно вектору τ, а ρ – двумерный вектор в плоскости (ω, τ)=0. В скалярном виде эта плоскость задается уравнением
![]() (3.52)
(3.52)
Для упрощения дальнейших выкладок удобно в частном пространстве с осями u, v, ω ввести вращающуюся систему координат ![]() , таким образом, чтобы ось ω была всегда направлена вдоль вектора τ. Оси uτ, vτ в этом случае лежат в плоскости (3.52), а их направление задается азимутальным углом φ. Связь этих систем координат определяется соотношениями
, таким образом, чтобы ось ω была всегда направлена вдоль вектора τ. Оси uτ, vτ в этом случае лежат в плоскости (3.52), а их направление задается азимутальным углом φ. Связь этих систем координат определяется соотношениями
![]() (3.53)
(3.53)
 (3.54)
(3.54)
В новых координатах теорема о центральном слое (3.51) перепишется следующим образом:
![]() (3.55)
(3.55)
При изменении направления проецирования τ модно последовательно заполнить частотное пространство спектрами проекций, сумму которых можно рассматривать как некоторый трехмерный фурье-образ:
![]() (3.53а)
(3.53а)
Во вращающейся системе координат это выражение преобразуется к виду:
![]() (3.53б)
(3.53б)
где Г – область изменения вектора τ.
Используя теорему (3.51), получаем:
![]() (3.56)
(3.56)
Таким образом, выражение (3.56) приводит к уравнению:
![]() (3.57)
(3.57)
где функция H зависит от области изменения вектора τ.
![]() (3.58)
(3.58)
По аналогии с двумерным случаем назовем функцию S(ω) спектром трехмерного суммарного изображения s(x). Тогда из (3.57), (3.58) следует, что
![]() (3.59)
(3.59)
![]() (3.60)
(3.60)
где ![]() - значок операции трехмерной свертки; h(x) – трехмерная искажающая функция.
- значок операции трехмерной свертки; h(x) – трехмерная искажающая функция.
Соотношения (3.55) – (3.58) позволяют получить алгоритмы восстановления трехмерных томограмм. Из уравнения (3.57), связывающего спектр суммарного изображения со спектром искомого изображения (3.57), имеем
![]() (3.61)
(3.61)
Данное выражение справедливо для тех ω, в которых H(ω)≠0.
Выполняя обратное преобразование Фурье над (3.61) получаем метод восстановления трехмерных томограмм из трехмерного суммарного изображения.
Подставляя в (3.61) выражение для спектра суммарного изображения через спектр проекций (3.55), находим
 (3.62)
(3.62)
Во вращающейся системе координат это выражение преобразуется к виду
 (3.62а)
(3.62а)
Отсюда трехмерная томограмма вычисляется обратным преобразованием Фурье:
![]()
Выполним замену координат u, v, ω на ![]() . Учитывая, что dudvdω =
. Учитывая, что dudvdω = ![]() , а также используя фильтрующее свойство δ-функций получаем
, а также используя фильтрующее свойство δ-функций получаем
![]() (3.63)
(3.63)
где xτ, yτ – пространственные координаты во вращающейся системе координат:
![]() (3.64)
(3.64)
Обозначив внутренний интеграл в (3.63) через ![]() окончательно имеем
окончательно имеем
![]() (3.65)
(3.65)
Данный алгоритм модно назвать алгоритмом суммирования двумерных фильтрованных обратных проекций. Действительно, для восстановления трехмерной томограммы по (3.65) необходима следующая операция:
1. регистрация двумерных проекций ![]() в плоскости xτyτ, перпендикулярной вектору τ.
в плоскости xτyτ, перпендикулярной вектору τ.
2. фильтрация двумерных проекций в той же плоскости xτyτ. Закон фильтрации определяется выражением (3.63). В частотном пространстве данной операции соответствует операция умножения двумерного спектра проекций ![]() на фильтр
на фильтр
 (3.66)
(3.66)
который определяется областью изменения Г вектора τ. Фильтрованная проекция равна
![]() (3.67)
(3.67)
3. трехмерное обратное проецирование. Эта операция формально состоит в замене координат xτ, yτ на xy по закону (3.64). Физический смысл обратного проецирования, как и в двумерном случае, заключается в «растяжении» двумерных проекций в направлении, совпадающим с направлением их проецирования, т.е. τ или zτ. Только в данном случае обратная проекция трехмерна и постоянна вдоль третьей оси zτ.
4. суммирование всех обратных фильтрованных проекций по угловым координатам, т.е. вычисление интеграла по dτ. Здесь надо различать два случая. В первом случае область Г является двумерной областью, т.е. вектор τ «заметает» объемную фигуру или, принимает все положения на сфере направлений. В этом случае ![]() . Во втором случае область Г является одномерной. Вид ее определяется траекторией измерения конца вектора τ на сфере направлений (рисунок 3.5), которую можно задать с помощью зависимости
. Во втором случае область Г является одномерной. Вид ее определяется траекторией измерения конца вектора τ на сфере направлений (рисунок 3.5), которую можно задать с помощью зависимости ![]() или
или ![]() . Тогда
. Тогда
![]() (3.68)
(3.68)
где ![]() ;
; ![]() .Фильтры G в этих случаях будут различны, так как они зависят от области Г. Таким образом, для восстановления трехмерной томограммы в общем случае требуется интегрирование только по одному из углов θ или φ. Однако первый случай также имеет право на существование, так как при этом улучшается помехоустойчивость результатов восстановления из-за переизбыточности информации о проекциях.
.Фильтры G в этих случаях будут различны, так как они зависят от области Г. Таким образом, для восстановления трехмерной томограммы в общем случае требуется интегрирование только по одному из углов θ или φ. Однако первый случай также имеет право на существование, так как при этом улучшается помехоустойчивость результатов восстановления из-за переизбыточности информации о проекциях.
Определим далее вид восстанавливающего фильтра G для ряда конкретных областей Г.
1. Пусть область Г – вся сфера направлений. Для вывода уравнения фильтра (3.63) необходимо вычислить интеграл (3.55), который в этом случае равен
 (3.69)
(3.69)
Произведя в (3.66) замену координат ![]() , получаем
, получаем
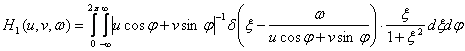
Используя фильтрующее свойство δ-функции находим, что
 (3.70)
(3.70)
т.е. функции H1 обладает сферической симметрией, поэтому ее вид не зависит от угловой ориентации декартовых координатных осей. Тогда
![]() (3.71)
(3.71)
таким образом, в том случае, когда область Г двумерна, восстанавливающий фильтр является двумерным ρ-фильтром, а выражение для трехмерной томограммы (3.65) равно

2. Рассмотрим одномерную область Г. Пусть она будет окружностью большого круга «сферы направлений» (рис.3.5). Данную траекторию можно описать зависимостью ![]() . Тогда из (3.65) следует, что
. Тогда из (3.65) следует, что ![]() и, следовательно, функция Н в (3.66) равна
и, следовательно, функция Н в (3.66) равна

произведя вычисления аналогично предыдущему случаю для Н1, получаем
![]() (3.72)
(3.72)
Подставляя в (3.69) соотношения (3.51) при условии ![]() , находим, что
, находим, что
![]() (3.73)
(3.73)
т.е. данный двумерный фильтр по одной оси uτ является одномерным ρ-фильтром, а по другой оси vτ он постоянен. На рисунке 3.13 схематично представлен вид фильтра. Назовем фильтр типа G2 цилиндрическим ρ-фильтром, а ось, вдоль которой он постоянен (у нас ось vτ, -- осью фильтра.

Рисунок 3.13 – Цилиндрический r-фильтр
 |
Рисунок 3.14 – Произвольная траектория сканирования трехмерного объекта
Таким образом, при линейной траектории проецирования требуется фактически одномерная фильтрация двумерных проекций цилиндрическим ρ-фильтром.
Рассмотрим также одномерную область Г. Пусть она является окружностью, не совпадающей с любой большой окружностью «сферы направлений». В этом случае вектор τ описывает конус. Данная траектория определяется зависимостью ![]() . Согласно (3.68)
. Согласно (3.68) ![]() и поэтому функция Н в (3.66) равна
и поэтому функция Н в (3.66) равна

Введем в плоскости (u, v) полярные координаты (ρ, ψ). Тогда Н3 приводится к виду

Так как результат интегрирования не зависит от ψ, то Н3 обладает цилиндрической симметрией. Тогда
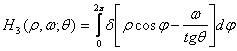
для вычисления этого интеграла используем следующее свойство δ-функций:
![]() (3.74)
(3.74)
где ![]() причем
причем ![]()
в нашем случае ![]() и уравнение
и уравнение ![]() имеет корни только тогда, когда
имеет корни только тогда, когда
![]()
При выполнении этого условия, используя свойство (3.74), для Н3 имеем

Окончательно можно записать следующее
 (3.75)
(3.75)
Видно, что функция Н3 внутри конуса ![]() равна нулю. Как следует из выражения (3.57), это приводит к искажению восстановленной томограммы, так как в этом случае теряется информация о той части спектра объекта, которая лежит в области
равна нулю. Как следует из выражения (3.57), это приводит к искажению восстановленной томограммы, так как в этом случае теряется информация о той части спектра объекта, которая лежит в области ![]() . Эта проблема получила название «missing cone problem». Физически эта проблема заключается в том, что при определенных схемах зондирования не могут быть зарегистрированы проекции для углов θ, которые больше некоторой величины, в нашем случае
. Эта проблема получила название «missing cone problem». Физически эта проблема заключается в том, что при определенных схемах зондирования не могут быть зарегистрированы проекции для углов θ, которые больше некоторой величины, в нашем случае ![]() . Поэтому спектрами проекций заполняется лишь часть частотного пространства.
. Поэтому спектрами проекций заполняется лишь часть частотного пространства.
Задача восстановления томограмм по неполным данным о проекциях для двумерного случая будет рассмотрена ниже. Она фактически сводится к задаче восстановления функции по ее неполно заданному спектру. Задача эта некорректная, и для ее решения применяют различные численные методы. Отвлекаясь от решения проблемы «missing cone», найдем аналитический вид восстанавливающего фильтра G3 для данного случая.
Записывая функцию Н3 во вращающейся системе координат при условии ![]() , получим
, получим
![]() (3.76)
(3.76)
Таким образом, при круговой траектории проецирования восстанавливающий фильтр является цилиндрическим ρ-фильтром, однако ориентация его отлична от ориентации фильтра G2. Ось фильтра G3, вдоль которой он постоянен, совпадает с осью uτ, т.е. она перпендикулярна цилиндрической оси фильтра G2.
3. Рассмотрим произвольную одномерную область Г. Пусть она описывается зависимостью ![]() . В этом случае конец вектора τ описывает на «сфере направлений» некоторую линию Г (рисунок 3.7). Функция Н будет равна
. В этом случае конец вектора τ описывает на «сфере направлений» некоторую линию Г (рисунок 3.7). Функция Н будет равна

Для вычисления этого интеграла используем свойство δ-функций (3.74). Уравнение ![]() приводит к следующему уравнению для углов θ:
приводит к следующему уравнению для углов θ:
![]() (3.77)
(3.77)
где ![]() . Данное уравнение имеет простую геометрическую интерпретацию. Используем тот факт, что уравнению (3.77) удовлетворяют лишь те углы
. Данное уравнение имеет простую геометрическую интерпретацию. Используем тот факт, что уравнению (3.77) удовлетворяют лишь те углы ![]() , при которых одновременно выполняются равенство (3.77) и тождество
, при которых одновременно выполняются равенство (3.77) и тождество ![]() . Первое равенство (3.77) определяет в пространстве координат u, v, ω плоскость, проходящую через начало координат. Нормаль к этой плоскости имеет полярный
. Первое равенство (3.77) определяет в пространстве координат u, v, ω плоскость, проходящую через начало координат. Нормаль к этой плоскости имеет полярный ![]() и азимутальный
и азимутальный ![]() углы. Вторая зависимость на единичной «сфере направлений» в частотном пространстве изображается линией Г. Поэтому корнями уравнения (3.77) являются полярные углы
углы. Вторая зависимость на единичной «сфере направлений» в частотном пространстве изображается линией Г. Поэтому корнями уравнения (3.77) являются полярные углы ![]() единичного вектора τ, выраженные через частотные координаты точек пересечения линии Г с окружностями больших кругов; ориентированных в пространстве координат u, v, ω (см. рис. 3.7). Нетрудно проверить, что 2-й и 3-й случаи также укладываются в данную интерпретацию.
единичного вектора τ, выраженные через частотные координаты точек пересечения линии Г с окружностями больших кругов; ориентированных в пространстве координат u, v, ω (см. рис. 3.7). Нетрудно проверить, что 2-й и 3-й случаи также укладываются в данную интерпретацию.
Согласно свойству (3.74) для вычисления Н4 необходимо также знать значения производной функции ![]() в точках
в точках ![]() :
:
![]()
Выражая ω через ![]() из равенства (3.74) и подставляя результат в
из равенства (3.74) и подставляя результат в ![]() , получаем
, получаем
![]()
После несложных тригонометрических преобразований, находим
 (3.78)
(3.78)
где
![]() (3.79)
(3.79)
Тогда
 (3.80)
(3.80)
Выражая ![]() через координаты (
через координаты (![]() ) при условии
) при условии ![]() , окончательно имеем
, окончательно имеем
 (3.81)
(3.81)
Видно, что и в общем случае восстанавливающий фильтр распадается на сумму слагаемых, каждое из которых зависит от модуля линейной комбинации частот ![]() и
и ![]() , а также сложным образом от тригонометрической комбинации этих координат. Из (3.78) следует, что эти составляющие постоянные вдоль некоторых направлений, которые определяются углами
, а также сложным образом от тригонометрической комбинации этих координат. Из (3.78) следует, что эти составляющие постоянные вдоль некоторых направлений, которые определяются углами ![]() с осью
с осью ![]() из соотношений
из соотношений
![]() (3.82)
(3.82)
Вид фильтра G4 существенно упрощается, если потребовать монотонности функции ![]() во всем диапазоне изменения угла θ. В этом случае для любого направления проецирования
во всем диапазоне изменения угла θ. В этом случае для любого направления проецирования ![]() плоскость, перпендикулярная к τ, пересекает линию Г на «сфере направлений» лишь один раз – в точке, положение которой определяется вектором, ортогональным вектору τ. Поэтому уравнение (3.74) удовлетворяют углы
плоскость, перпендикулярная к τ, пересекает линию Г на «сфере направлений» лишь один раз – в точке, положение которой определяется вектором, ортогональным вектору τ. Поэтому уравнение (3.74) удовлетворяют углы ![]() , определяющие направление проецирования τ. В этом случае в выражении для фильтра G4 (3.78) остается одно слагаемое от суммы
, определяющие направление проецирования τ. В этом случае в выражении для фильтра G4 (3.78) остается одно слагаемое от суммы ![]() . Тогда имеем
. Тогда имеем
![]() (3.83)
(3.83)
т.е. данный фильтр является цилиндрическим ρ-фильтром, постоянным вдоль оси, составляющий угол ![]() с осью v.
с осью v.
Еще до появления методов современной вычислительной томографии была широко распространена так называемая классическая томография . Иногда данный тип томографии называют также продольной томографией, томографией фокальной плоскости и т. д.
Классическая томография является чисто аналоговым методом восстановления информации о внутренней, структуре объектов, суть которого заключается в следующем. Источник зондирующего излучения 1 (рисунок 3.15) и регистратор 3 движутся навстречу друг другу в параллельных плоскостях А и С. Изображение плоскости В внутри объекта 2, в котором лежит точка пересечения осей зондирующего пучка, на регистраторе 3 будет неподвижным. Изображения любой другой плоскости объекта будут смещаться по регистратору 3 при одновременном движении, пары источник — регистратор. Поэтому на регистраторе записывается сумма четкого изображения сечения В («фокального» сечения) и смазанных движением остальных сечений объекта, которые создают низкочастотный фон.
 |
Рисунок 3.15 – Схема классической томографии с линейным перемещением
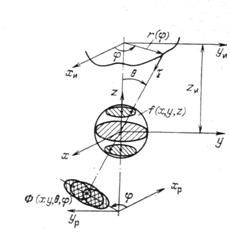 |
Рисунок 3.16 - Схема классической томографии с произвольной плоской траекторией сканирования
Траектория движения источника 1 могут быть и одномерными (линейными), и двумерными. Модели классических томографов описаны в (1,46). Многие из них до настоящего времена широко попользуются, на практике из-за простоты, дешивизны, малой дозы облучения. Поэтому представляет интерес задача математического описания методов восстановления изображений в классических томографах с целью нахождения способов улучшения их качества. Это позволит повысить диагностическую ценность классических томограмм.
В настоящем параграфе мы распространим этот подход на случай произвольной двумерной траектории перемещения источника
На рисунке 3.16 приведена схема зондирования и записи проекций трехмерного объекта f(x, у, z) в классических томографах с перемещением источника и регистратора. Предполагаем, что источники зондирующего излучения и регистраторы движутся или располагаются в плоскостях, параллельных, например плоскости ху объекта. Оси зондирующих пучков пересекаются в начале систему координат x, у, z, связанной с объектом. Предполагаем также, что плоскость источника находится на таком расстоянии от объекта, что можно считать зондирующий пучок в области объекта параллельным. Положение источника можно описать двумя углами θ и φ или же его траекторией ![]() , где r, φ —полярные координаты в плоскости источника, связанные с угловыми координатами соотношением
, где r, φ —полярные координаты в плоскости источника, связанные с угловыми координатами соотношением
![]()
где zи — расстояние от центра объекта до плоскости источника.
При описанной схеме зондирования выражение для двумерной проекций запишется в виде
![]() (3.84)
(3.84)
Данная формула для проекции имеет, простой геометрический смысл. Если трехмерный объект разбить на слои z = const, то проекция просто равна сумме данных слоев, сдвинутых соответствующим образом. Величина сдвига слоя z = const вдоль оси x равна ![]() , а вдоль оси у —
, а вдоль оси у — ![]() .
.
Заметим, что при такой записи все проекции лежат в одной и той же плоскости, параллельной ху. Применив двумерное преобразование Фурье к правой и левой частям (3.84), получим
![]() (3.85)
(3.85)
Сделаем замену координат ![]() , тогда из (3.85) Следует
, тогда из (3.85) Следует
![]()
Сравнивая полученное выражение с определением трехмерного преобразования Фурье исходной функции f(x, у, z)
![]()
Получаем теорему о центральном слое для. двумерных проекций, зарегистрированных в плоскости xy:
![]() (3.86)
(3.86)
Смысл данной теоремы заключается в том, что для каждого направления зондирования θ, φ значение фурье-спектра проекции ![]() в любой точке с координатами и, v совпадает со значением трехмерного фурье-спектра исходной функции F(u, v, w) в точке с координатами
в любой точке с координатами и, v совпадает со значением трехмерного фурье-спектра исходной функции F(u, v, w) в точке с координатами ![]() . Геометрическое место таких точек есть плоскость, проходящая через начало системы координат u, v, w, нормаль к которой имеет угловые координаты θ, φ.
. Геометрическое место таких точек есть плоскость, проходящая через начало системы координат u, v, w, нормаль к которой имеет угловые координаты θ, φ.
Таким образом, для заполнения всего трехмерного пространства с осями u, v, w значениями спектра F(u, v, w) необходимо значения каждой проекции ![]() спроецировать вдоль оси w из плоскости w=0 на плоскость
спроецировать вдоль оси w из плоскости w=0 на плоскость ![]() . Можно также сказать, что, увеличив масштаб спектра каждой проекции на величину
. Можно также сказать, что, увеличив масштаб спектра каждой проекции на величину ![]() вдоль одного, направления, составляющего угол φ с осью u, мы получим значения трехмерного спектра объекта вдоль сечения
вдоль одного, направления, составляющего угол φ с осью u, мы получим значения трехмерного спектра объекта вдоль сечения ![]() . Данная интерпретация теоремы о центральном слое несколько отличается от традиционной (3.51) вследствие того, что мы оперируем проекциями вида (3.84), которые регистрируются не в плоскости, перпендикулярной оси зондирующего пучка, а всегда в одной и той же плоскости, параллельной (х, у).
. Данная интерпретация теоремы о центральном слое несколько отличается от традиционной (3.51) вследствие того, что мы оперируем проекциями вида (3.84), которые регистрируются не в плоскости, перпендикулярной оси зондирующего пучка, а всегда в одной и той же плоскости, параллельной (х, у).
В данном параграфе при выводе уравнения классической томограммы мы не будем принимать во внимание физический механизм взаимодействия зондирующего излучения с объектом и регистратором. При строгом рассмотрении необходимо учитывать, что зондирующее излучение интенсивности I0, пройдя поглощающий объект f(x, у, z) под направлением τ ослабляется согласно закону Бугера в ![]() раз. А так как регистратор расположен под углом к оси зондирующего пучка, то зарегистрированное на нем изображение при одном из положений источника будет пропорционально величине
раз. А так как регистратор расположен под углом к оси зондирующего пучка, то зарегистрированное на нем изображение при одном из положений источника будет пропорционально величине
![]()
где Ф определено уравнением (3.84). Для самосветящихся объектов без поглощения собственного излучения нами не учитывается лишь наклонное падение излучения на регистратор.
При описанных упрощениях считаем, что в классическом томографе при движении источника на регистраторе суммируются проекции (3.84) по направлениям τ. Обозначим данное изображение через k(x, y). Тогда можно записать, что
![]() (3.87)
(3.87)
где Г – траектория движения источника, заданная в виде плоской кривой ![]() ; dτ определяется соотношением (3.68).
; dτ определяется соотношением (3.68).
Нетрудно видеть из теоремы о центральном слое (3.86), что двумерный фурье-образ K(u,v) функции k(x,y) связан со спектром объекта следующим уравнением:
![]()
С точностью до коэффициента ![]() , которым мы уже пренебрегли при упрощении физической модели классического томографа, внутренний интеграл совпадает с функцией Н из равенства (3.58). Тогда
, которым мы уже пренебрегли при упрощении физической модели классического томографа, внутренний интеграл совпадает с функцией Н из равенства (3.58). Тогда
![]()
Следовательно,
![]() (3.88)
(3.88)
т. е. классическая томограмма в некотором приближении описывается сечением трехмерного суммарного изображения. Из выражений (3.88) и (3.59) вытекает связь классической томограммы с исходной функцией объекта:
![]() (3.89)
(3.89)
где ![]() -- значок двумерной свертки по осям x, y. Таким образом, вид искажающей функции h определяет степень отличия классической томограммы k от самого объекта f.
-- значок двумерной свертки по осям x, y. Таким образом, вид искажающей функции h определяет степень отличия классической томограммы k от самого объекта f.
Саму искажающую функцию получим простым обратным преобразованием Фурье от функций (3.70), (3.72), (3.73).
1. Рассмотрим двумерную область Г. Ниже будет показано, что данная схема зондирования реализуется в оптических схемах при построении изображений трехмерных объектов. В этом случае функция h равна
![]() (3.90)
(3.90)
Отметим, что по сравнению с двумерным случаем искажающая функция трехмерного суммарного изображения несколько уже. Здесь функция h1 спадает как ![]() , где
, где ![]() , а в двумерном случае – как
, а в двумерном случае – как ![]() . Этот факт также следует из вида фильтра (3.70), который показывает, что заполнение частотного пространства спектрами проекции для данной траектории зондирования происходит более равномерно.
. Этот факт также следует из вида фильтра (3.70), который показывает, что заполнение частотного пространства спектрами проекции для данной траектории зондирования происходит более равномерно.
2. Рассмотрим линейную траекторию источника. В этом случае
![]()
Будем проводить вычисление интеграла во вращающейся системе координат ![]() . Тогда
. Тогда

Отсюда следует, что искажающая функция будет равна
 (3.91)
(3.91)
т.е. ее вид в координатах ![]() совпадает с искажающей функцией в двумерном случае.
совпадает с искажающей функцией в двумерном случае.
3. Рассмотрим траекторию источника в виде окружности. Как следует из (3.75), фильтр Н3 обладает цилиндрической симметрией относительно оси w. Поэтому будем вычислять функцию h3 в цилиндрических координатах r, z, где ![]() :
:

где J0(x) – функция Бесселя нулевого порядка. Для вычисления интеграла по w воспользуемся следующим равенством:

Тогда получим, что

Используя еще одно свойство функции Бесселя

окончательно имеем
 (3.92)
(3.92)
Представляет самостоятельный интерес задача получения методов обработки проекций, регистрируемых в классических томографах, а также самих классических томограмм с целью синтеза по ним точных изображений слоев трехмерного объекта, т.е. томограмм в современном понимании этого термина.
Для вывода алгоритмов восстановления томограмм по проекциям, регистрируемым в классических томографах, воспользуемся следующим формальным приемом. В выражении для трехмерного обратного преобразования Фурье
![]() (3.93)
(3.93)
сделаем замену координаты w на θ по закону
![]()
Так как интеграл по w имел бесконечные пределы интегрирования, то, следовательно, надо потребовать, чтобы для любых фиксированных u, v величина tgθ изменялась также от -∞ до +∞. Поэтому необходимо, чтобы ![]() . Для упрощения дальнейших рассуждений потребуем также, чтобы зависимость
. Для упрощения дальнейших рассуждений потребуем также, чтобы зависимость ![]() была монотонной на всем интервале изменения θ.
была монотонной на всем интервале изменения θ.
Якобианом такого преобразования служит функция ![]() . При этом величина φ может быть или параметром, или функцией от угла θ. Используя теорему о центральном слое (3.83), из (3.90) получаем
. При этом величина φ может быть или параметром, или функцией от угла θ. Используя теорему о центральном слое (3.83), из (3.90) получаем

Обозначая через
![]()
так называемые «фильтрованные» двумерные проекции, выражение для f можно переписать в виде
 (3.94)
(3.94)
Полученное выражение аналогично по своей структуре формуле (3.65), выражающей алгоритм суммирования фильтрованных обратных проекций. Таким образом, для восстановления двумерной томограммы слоя z=const необходимо над проекциями ![]() выполнить следующие операции:
выполнить следующие операции:
1) фильтрацию проекций, т.е. переход от ![]() к
к ![]() ;
;
2) обратное проецирование, т.е. замену координат x на ![]() , каждой проекций на величину
, каждой проекций на величину ![]() вдоль оси x и на
вдоль оси x и на ![]() вдоль оси y. Отметим, что для восстановления томограммы слоя z=0 необходимо совместить все проекции без сдвига;
вдоль оси y. Отметим, что для восстановления томограммы слоя z=0 необходимо совместить все проекции без сдвига;
3) суммирование всех преобразованных проекций ![]() .
.
Модуль якобиана преобразования координат определяет вид фильтра для спектра проекций. В том случае, когда задана зависимость ![]() , этот фильтр имеет вид
, этот фильтр имеет вид
![]() (3.92)
(3.92)
для линейной траектории ![]() фильтр равен
фильтр равен
![]() (3.96)
(3.96)
Удобно воспользоваться записью якобиана через выражение траектории источника
В этом случае получаем, что
![]()
где ![]() . Если ввести обозначения
. Если ввести обозначения ![]() ,
, ![]() , то
, то
![]()
т.е. выражение (3.95) преобразуется к виду цилиндрического ρ-фильтра, амплитуда которого для каждого угла θ равна ![]() , а ось повернута на угол β(θ) относительно оси v.
, а ось повернута на угол β(θ) относительно оси v.
Траектория источника ![]() описывает некоторую плоскую линию в плоскости источника z=zи. Угол γ между касательной и данной кривой в любой точке
описывает некоторую плоскую линию в плоскости источника z=zи. Угол γ между касательной и данной кривой в любой точке ![]() плоскости xy и осью x определяется выражением
плоскости xy и осью x определяется выражением
![]()
Следовательно, угол. поворота оси ρ-фильтра совпадает с углом касательной к траектории и осью х. Таким образом, мы показали, что для любой траектории источника двумерные проекции обрабатываются цилиндрическим ρ-фильтром, который, по сути, является одномерным. Ориентирован этот фильтр для каждой проекции по-разному, а именно по направлению касательной к траектории в данной точке. Как было показано выше, необходимым условием замены w на θ в интеграле (3.93) является требование ![]() . Однако часто
. Однако часто ![]() , так как на практике не всегда удается реализовать такие схемы зондирования. Это приводит к искажению восстановленной томограммы, так как теряется информация о той части спектра объекта, которая лежит в области
, так как на практике не всегда удается реализовать такие схемы зондирования. Это приводит к искажению восстановленной томограммы, так как теряется информация о той части спектра объекта, которая лежит в области ![]() . Для случая линейной траектории данная проблема «missing cone» является двумерной. Для более сложных траекторий она трехмерна. Видно, что область, не заполненная значениями проекций, является конусом, что и определило название данной проблемы.
. Для случая линейной траектории данная проблема «missing cone» является двумерной. Для более сложных траекторий она трехмерна. Видно, что область, не заполненная значениями проекций, является конусом, что и определило название данной проблемы.
До сих пор, рассматривая замену координат по закону ![]() , мы предполагали, что переменная w заменяется на угловую переменную θ. Однако формально можно делать замену w на другую угловую переменную φ. В этом случае якобиан преобразования координат будет равен
, мы предполагали, что переменная w заменяется на угловую переменную θ. Однако формально можно делать замену w на другую угловую переменную φ. В этом случае якобиан преобразования координат будет равен
![]()
Рассмотрим также такую траекторию, когда ![]() . Более сложные траектории
. Более сложные траектории ![]() уже фактически были рассмотрены ранее как траектории, которые описываются функцией, обратной к
уже фактически были рассмотрены ранее как траектории, которые описываются функцией, обратной к ![]() . Траектория
. Траектория ![]() является окружностью радиуса
является окружностью радиуса ![]() . Нетрудно сразу же получить аналитический вид фильтра из выражения для якобиана.
. Нетрудно сразу же получить аналитический вид фильтра из выражения для якобиана.
![]()
Необходимо помнить, что данный фильтр получен для области ![]() .
.
Видно, что данный фильтр, так же как и фильтры для остальных траекторий, является цилиндрическим ρ-фильтром, направление оси которого совпадает с направлением касательной к окружности, т.е. ось фильтра для любого угла φ перпендикулярна к радиусу окружности, проведенному под углом φ.
В заключение покажем возможность реставрации изображения сечения из классической томограммы, полученной в томографе с линейной траекторией пары источник-регистратор.
Перепишем выражение (3.94) для томограммы для z=0:
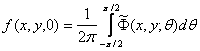
Фильтр проекций в этом случае определяется функцией (3.96). Пусть φ=0, тогда данный фильтр равен
![]()
и, следовательно

Внутренний интеграл с точностью до коэффициента ![]() есть спектр суммарного изображения K2(u,y), который и описывает данную классическую томограмму, так что можно приближенно записать
есть спектр суммарного изображения K2(u,y), который и описывает данную классическую томограмму, так что можно приближенно записать
![]()
где функция ![]() обозначает одномерно отфильтрованную по оси x классическую томограмму.
обозначает одномерно отфильтрованную по оси x классическую томограмму.
Таким образом, после одномерной ρ-фильтрации функция ![]() вдоль направления движения источника и регистратора можно ожидать некоторого улучшения качества полученной томограммы.
вдоль направления движения источника и регистратора можно ожидать некоторого улучшения качества полученной томограммы.
Исходя из этих предпосылок, был проведен эксперимент, подтверждающий возможность реставрации изображений сечений из классических томограмм. На рисунке 3.10,а приведена обычная продольная томограмма черепа, полученная при прямолинейной траектории сканирования. С помощью телевизионного устройства ввода изображений в ЭВМ эта томограмма оцифровывалась. Одномерная фильтрация проводилась в ЭВМ СМ-4 ρ-фильтром, аподизированным гауссианной.
На рисунке 3.17,б приведена реставрированная томограмма. Видно, что в результате фильтрации устранен характерный для данного типа томограмм «смаз» и произошло подчеркивание мелких деталей на изображении.
 |
 |
||
а) б)
Рисунок 3.17 – Классическая томограмма (а)б результат одномерной фильтрации классической томограммы (б)
В предыдущих параграфах настоящей главы приведен аналитический аппарат томографии, который указывает на принципиальную возможность решения обратной задачи восстановления изображения по проекциям. При создании конкретной томографической системы в качестве одной из основных задач выдвигается разработка вычислительного алгоритма, реализующего тот или иной метод реконструкции томограммы.
При решении задачи восстановления распределения физических величин по проекционным измерениям, как и при решении любой другой обратной задачи возникают два вопроса: достаточно ли исходных данных для последующего анализа, т.е. правильно ли поставлен физический эксперимент и существует ли аналитическая либо вычислительная процедура, позволяющая получить однозначный ответ. При решении обратных задач необходимо так же учитывать влияние ошибок измерения экспериментальных данных.
В начале 20 века французский математик Ж. Адамар ввел термин некорректной задачи. Решение подобных задач очень чувствительно к малым ошибкам исходных данных или вычислений, т.е. их небольшие отклонения приводят к значительным изменениям ответов.
В последние годы обратные задачи стали встречаться в практике анализов данных очень часто, поэтому возникла необходимость в разработки методов решения некорректных задач. Общим во всех известных методах решения является привлечение некоторых дополнительных данных об ответе, т.е. в тех случаях, когда при определении ответа происходит сильное увеличение ошибок, в алгоритм вводятся новые ограничения, которые делают задачу более устойчивой.
Такая дополнительная информация о решении выбирается, как правило, из априорных данных об объекте исследования. Однако в вычислительной математике были разработаны более общие процедуры решения таких задач, которые носят достаточно универсальный характер. В их основу положен метод регуляризации, разработанный А. Н. Тихоновым.Суть метода регуляризации заключается в том, что, во-первых, формулируются дополнительные условия на решение, задачи и, во-вторых, строится формальный алгоритм, который исключает возникновение, неустойчивого решения.
В случае реконструктивной томографии методы регуляризации применяются для решения задачи деконволюции свертки. Мы не будем рассматривать конкретные виды регуляризующих алгоритмов, применяемых в рентгеновской медицинской томографии.
Другим алгоритмом восстановления томограмм является алгебраический. Он применяется в том случае, когда задача томографии описывается в дискретной форме. При этом изображение сечения объекта разбивается двумерной декартовой сеткой, в каждом узле которой ищется значение функции. Проекционные данные представляют собой сумму значений искомой функции, умноженных на весовые множители, которые учитывают вклад площади каждого соответствующего элемента изображения в луч-сумму. В результате мы получаем систему линейных уравнений, при этом число уравнений соответствует количеству луч-сумм, а число неизвестных — количеству элементов разбиения в томограмме.
Дискретизация области реконструкции изображения возможна не только на декартовой сетке. Применяются различные методы представления. На этом базируются методы восстановления томограмм, основанные на разложении в конечные ряды. Наиболее широко распространены алгоритмы реконструкции с использованием интегральных преобразований. Они основаны на нахождении формулы обращения, т. е. определении томограммы из проекционных данных и затем реализации ее вычисления на ЭВМ. При этом учитываются особенности схемы сбора данных, зашумленность изображения и т. д. Фактически в большинстве случаев задача сводится к построению вычислительной процедуры, реализующей методы восстановления (фурье-синтез, суммирование фильтрованных обратных проекций, фильтрация суммарного изображения). К этому же классу следует отнести алгоритмы, непосредственно использующие инверсное преобразование Радона. Метод интегральных преобразований дает базу для множества разнообразных алгоритмов, часть из которых используется в коммерческих медицинских томографах. Применение той или иной формулы обращения и соответствующего ей вычислительного алгоритма определяется, как правило, спецификой конкретной задачи.
В заключение заметим только, что в задачах оптической томографии при огромном многообразии исследуемых объектов и схем сбора данных, поиск каких-либо универсальных алгоритмов является слишком сложной задачей. На наш взгляд, поиск в этой области должен быть направлен в сторону разработки таких алгоритмов, которые позволяют, во-первых, привлекать самую разнообразную априорную информацию (иногда плохо формализованную) и, во-вторых, учитывать такие особенности системы регистрации проекционных данных, как малоракурсность, ограниченный угол обзора и т.д.
На рисунке 3.18 представлен объект исследования и его спектр.

Рисунок 3.18
Введем следующие параметры:
D – диаметр объекта - томограммы;
d – интервал пространственной дискретизации проекции;
Dj – интервал угловой дискретизации, т.е. шаг по углу при получении проекций;
rmax – максимальная пространственная частота томограммы;
![]() , где
, где ![]() – число отсчетов в каждой проекции.
– число отсчетов в каждой проекции.
Интервал дискретизации определяется спектром объекта. Если мы хотим восстановить максимальную пространственную частоту rmax, то интервал пространственной дискретизации проекции формулой: ![]() (по теореме Котельникова).
(по теореме Котельникова).
Оценим интервал угловой дискретизации Dj. Фурье - образы проекций будут расположены в частотной плоскости с интервалом Dj под углом j +![]() (из теоремы о центральном слое). Из геометрии следует, что максимальный интервал дискретизации в частотной области будет равен:
(из теоремы о центральном слое). Из геометрии следует, что максимальный интервал дискретизации в частотной области будет равен:
![]() .
.
С другой стороны, применяя теорему Котельникова для пространственной области, получим:
![]() .
.
Сопоставляя последние два соотношения нетрудно получить уравнение для угловой дискретизации и числа проекций.
![]()
![]()
При реализации данного алгоритма необходимо сделать следующие операции:
1) Дискретная фильтрация проекций (дискретные решения некорректной обратной задачи)
2) Дискретное обратное проецирование
3) Суммирование
Метод суммирования может быть реализован различными «аналоговыми» устройствами. Например, можно использовать электронно-лучевую трубку, на экране которой последовательно отображают линии; их положение соответствует тем пучкам рентгеновского излучения, для которых производится измерение лучевых сумм. Информация с электронно-лучевой трубки суммируется на фотографической пленке, причем плотность почернения моделируется пропорционально величине лучевой суммы. Результирующее изображение на фотопленке будет представлять собой реконструкцию, полученную обратным проецированием.
Мы не будем рассматривать подобные аналоговые методы реконструкции. Наш интерес заключается в вычислении величины [Bp](r,f) по данным у, где уi = p(li, qi,) для 1 < i= I. Мы ограничим наше рассмотрение схемой сбора данных для М равномерно распределенных в пространстве параллельных лучей в каждом ракурсе. Пусть Dобозначает угол между направлениями ракурсов (так что D= p/М), a d — шаг между параллельными лучами. Пусть Nd > Е > r. На рисунке 3.19 показаны как точки, для которых величина p известна, так и прямая, вдоль которой необходимо проинтегрировать p, чтобы получить
 (3.97)
(3.97)
Метод, который обычно используют для численного определения величины данного интеграла, состоит из следующих двух этапов.

Рисунок 3.19 – Числовое значение оператора обратного проецирования производится по оценке линейного интеграла вдоль l=cos(J-j)
Сначала аппроксимируем правую часть выражения (3.97) суммой
![]() (3.98)
(3.98)
которую называют суммой Римана для данного интеграла, а затем производим оценку для каждого значения т величины p(rcos(mD —f), тD) по известным значениям p(nd, mD) ( — N£ п£ N) путем интерполирования.
В реконструктивной томографии обычно используют два метода интерполяции: метод интерполяции по ближайшему значению и метод линейной интерполяции. При интерполяции по ближайшему значению вычисляют p(rcos(mD —f), тD) по величинам p(nd, mD), где п выбирают таким образом, чтобы выражение ½nd — rcos(mD —f) ½ имело наименьшее возможное значение.
При линейной интерполяции п выбирают так, чтобы nd £ rcos(mD —f) < (п + l)d, и вычисляют p(rcos(mD —f), тD)по формуле
 (3.99)
(3.99)
Другими словами, определение [Bр](r, f) при помощи метода интерполяции по ближайшему значению выполняют следующим образом: складывают вместе лучевые суммы для лучей по одному из каждого ракурса, которые являются ближайшими к точке (r, f), и результат умножают на Д. Линейная интерполяция является несколько более сложной и дорогостоящей: вместо лучевых сумм одного луча складывают линейную интерполяцию лучевых сумм двух лучей, которые находятся по обеим сторонам от точки(r, f).
Чтобы получить дискретизированное изображение, вычисления повторяют для центральной точки каждого элемента изображения и полученный результат рассматривают как оценку плотности в данном элементе изображения. Такое дискретизированное изображение может быть представлено как J-мерный вектор-столбец ![]()
При таком методе можно получить дискретизированное изображение ![]() , средние плотности которого
, средние плотности которого ![]() существенно отличаются от средней плотности
существенно отличаются от средней плотности ![]() дискретизации х изображения, которое реконструируют. Так как обычно мы имеем достаточно хорошую оценку
дискретизации х изображения, которое реконструируют. Так как обычно мы имеем достаточно хорошую оценку ![]() величины х, то мы можем скорректировать это при помощи нормировки, которая может быть либо аддитивной, либо мультипликативной.
величины х, то мы можем скорректировать это при помощи нормировки, которая может быть либо аддитивной, либо мультипликативной.
Аддитивная нормировка позволяет получить дискретизированное изображение ![]() , у которого j-компонента равна
, у которого j-компонента равна
![]() (3.100)
(3.100)
 |
б - мультипликативная нормировка;
в - использование видоизмененного соотношения между яркостью и контрастом, позволяющего выделять детали на реконструкции
Рисунок 3.20 – Реконструкция стандартных проеционныхданных для параллельного пучка при помощи алгоритма непрерывного обратного проецирования с линейной интерполяцией

Рисунок 3.21 - Кривые распределения плотности вдоль 63 –го столбца для реконструкций, показанных на рисунке 3.20
Мультипликативная нормировка дает дискретизированное изображение, j-я компонента которого равна
![]() (3.101)
(3.101)
Последнее выражение применимо только тогда, когда ![]() . Отметим, что в любом случае средняя плотность
. Отметим, что в любом случае средняя плотность ![]() равна
равна![]() .
.
Интересное свойство мультипликативной нормировки состоит в том, что при ее проведении результат получает вновь правильную размерность. Это связано с тем, что величина ![]() имеет размерность обратной длины, так как получается суммированием с безразмерной величиной, деленной на сумму длин, в результате чего
имеет размерность обратной длины, так как получается суммированием с безразмерной величиной, деленной на сумму длин, в результате чего ![]() имеет правильную размерность. С другой стороны (3.100) почти не имеет физического смысла: величинах
имеет правильную размерность. С другой стороны (3.100) почти не имеет физического смысла: величинах ![]() равна разнице между величиной,_имеющей размерность обратной длины (х), и безразмерной величины (
равна разнице между величиной,_имеющей размерность обратной длины (х), и безразмерной величины (![]() ). По этой причине обычно рекомендуют пользоваться мультипликативной, а не аддитивной нормировкой.
). По этой причине обычно рекомендуют пользоваться мультипликативной, а не аддитивной нормировкой.
Методы, описанные выше, были использованы для стандартных проекционных данных в параллельном пучке с применением метода линейной интерполяции. Полученные результаты представлены на рисунке 3.20, а соответствующие кривые распределения плотности вдоль столбца 63 — на рисунке 3.21. Как видно из данных по столбцу, рассмотренные алгоритмы не применимы для исследования тканей внутри головы. Изображение на рисунке 3.20б выглядит черным. Это связано с принятым нами условием воспроизводить значения 0,1945 см-1 и меньше черным цветом. По этой причине мы воспроизводим данное изображение при другой установке соотношения между яркостью и контрастом на рисунке 3.20в. Меры различия между изображениями приведены в таблице 3.3.
Таблица 3.3 - Меры различия между изображениями и время счета на ЭВМ при «непрерывном» обратном проецировании реконструкций по стандартным проекционным данным для параллельного пучка
| Алгоритм нормировки d r e f |
| Аддитивный 14,6040 12.0195 3,9950 125 Мультипликативный 0,8111 0,5818 0,2731 125 |
В последнем разделе мы по получили дискретизированное изображение путем численного определения интеграла в выражении (3.97) для центральных точек элементов изображения. В качестве альтернативного подхода можно использовать алгоритм с разложением функции в ряд.
Рассмотрим базисные изображения, которые имеют значения 1 внутри элемента изображения и 0 вне. В этом случае ri,j равна вычисленной длине пересечения i-го луча с j-м элементом изображения. Приведенные ниже критерии описывают то, что следует ожидать из интуитивных соображений от реализации алгоритма обратного проецирования для элементов изображения:
а) луч должен давать вклад только в те элементы изображения, которые он пересекает, и не давать вклада в остальные;
б) вклад i-луча в элемент изображения должен быть пропорционален у, — измеренной лучевой сумме для i-го луча;
в) вклад i-го луча в j-й элемент изображения должен быть пропорционален ri,j.
Все эти критерии удовлетворяются, если мы используем для оценки плотности в ![]() в j-м элементе изображения выражение
в j-м элементе изображения выражение
![]() (3.102)
(3.102)
В матричном представлении это выражение можно записать следующим образом:
![]() (3.103)
(3.103)
где RT — транспонированная матрица R, т.е. матрица, у которой (i, j)-й элемент равен ri,j.
Соотношения, приведенные выше, не зависят от того, какие базисные функции приписаны элементам изображения. Мы полагаем в общем случае, что выражение (3.103) является решением дискретной реконструкционной задачи при использовании алгоритма обратного проецирования для заданной проекционной матрицы R. В частности, мы называем результат умножения 7-мерного вектора на RT дискретной обратной проекцией.
Точно так же, как и в случае алгоритма непрерывного обратного проецирования, средняя плотность х* может существенно отличаться от средней плотности в изображении, подлежащем реконструкции. В таком случае можно получить хороший результат, применяя аддитивную и мультипликативную нормировку . Это, конечно, имеет смысл, если разложение в ряд представляет собой дискретизированное выражение.
Дискретное обратное проецироание, определяемое выражением (3.103), можно использовать для любой схемы сбора данных. Для стандартных проекционных данных в параллельном пучке это приводит к результату, весьма сходному по внешнему виду с тем, что показано на рисунке 3.20. В том случае, когда дискретное обратное проецирование применяется для стандартных проекционных данных для веерного пучка, получают несколько
 |
а- аддитивная нормировка;
б – мультипликативная нормировка;
в – использование видоизмененного соотношения между яркостью и контрастом, позволяющего выделять детали на реконструкции
Рисунок 3.22 – Реконструкция стандартных проекционных данных для веерного пучка при помощи алгоритма дискретного обратного проецирования

Рисунок 3.23 - Кривые распределения плотности вдоль 63 –го столбца для реконструкций, показанных на рисунке 3.22
Таблица 3.3- Меры различия между изображениями и время счета на ЭВМ для реконструкций дискретного обратного проецирования по стандартным проекционным данным для
веерного пучка
| Алгоритм нормировки d r e t Аддитивный 80,5233 66,8735 25,2084 295 Мультипликативный 0,8109 0,5818 0,2727 297 |
отличные с виду результаты, которые приведены на рисунке 3.22. Кривая распределения плотности вдоль столбца 63 этих реконструкций дана на рисунке 3.23. Другие подробности, характеризующие алгоритм обратного проецирования, приведены в таблице 3.3.
Достоинством данных алгоритмов является их чрезвычайная продуктивность.
Итерационные алгоритмы представляют собой последовательное действие одной и той же операции, в результате которого находится решение. Достоинством данного алгоритма является появление возможности не вводить обратного оператора.
Итерационный алгоритм основан на том, что при реконструкции используются только известные данные о передаточной функции и нет необходимости в определении обратного оператора. В томографии итерационный алгоритм используется в тех случаях, когда существует ограниченный набор проекционных данных. В этом случае передаточная функция томографа равна нулю в больших областях пространственных частот.
Проекция задана только в пределах угла, а вне его равна нулю, картинка представлена на рисунке 3.24.
Итерационный алгоритм работает на привлечении априорной информации об объекте на всех этапах итерационного процесса.

Рисунок 3.24.
Итерационный алгоритм Гершберга
Итерационный алгоритм Гершберга используется в тех случаях, когда количество проекционных данных недостаточно для применения классических методов.
Достоинства метода:
1. Нет необходимости в определении оператора обратного оператору искажений, т.е. в процедуру восстановления используют тот оператор, который исказил изображение.
2. При выводе итерационного уравнения можно использовать известные свойства искомого решения, т.е. априорную информацию на каждом этапе итерационной процедуры.
Рассмотрим построение итерационной процедуры, представленной на рисунке 3.25.
 |
Рисунок 3.25
Пусть мы имеем некоторые функции и их Фурье–образ:

и сформируем из них звезду (рисунок 3.25), где за нулевую итерацию берется Фурье спектр ![]() (двумерная функция), получаемый Фурье-синтезом, тогда можно записать:
(двумерная функция), получаемый Фурье-синтезом, тогда можно записать:
![]()
![]()
где с – оператор априорной информации об объекте;
HN – функция «звезды».Она равна 1 на лучах и 0 вне лучей.
Берем первичную оценку информации, затем делам ЛФП используя априорную информацию. При умножении спектра на маску (0, где звезда существует, и 1, где ее нет).
SN – лучи, заданные правильно, а остальные в уравнении добавляет что-то, что будет вне звезды, между лучами.
Процедура состоит из следующих этапов:
1) По известному набору проекций вычисляется набор их одномерных Фурье-образов, которые по теореме о центральном сечении дают в частотной области значения Фурье-образов искомого решения (томограммы). На этом этапе значения спектральных амплитуд равны нулю вне данных лучей.
2) Выполняется обратное двумерное преобразование Фурье для получения оценки томограммы.
3) Вносится априорная информация о положительности функции и ограниченности области ее задания (оператор с).
4) Проводится прямое двумерное преобразование Фурье от оценки томограммы предыдущего шага и значения спектра на лучах, определяется на шаге 1, заменяются величинами, вычисленными ранее непосредственно по проекции.
5) Проверяются критерии окончания итерационной процедуры, если они не выполняются, то переход к этапу 2.
Критерий окончания итерации состоит в следующем: окончания итерационного процесса происходит, когда происходит равенство нормы отклонения одномерных и двумерных оценок Фурье-спектра объекта на лучах норме шума в проекциях.
Количество итераций приближенно 20-30 (в зависимости от сложности).
Схематично алгоритм Гершберга можно представить как итерационные переходы от оценки объекта в спектральной плоскости к оценке объекта в пространственной области с внесением априорной информации о каждой из областей.
В спектре области – это априорная информация – знание Фурье-спектра на лучах. В пространственной области — знание о положительности и ограниченности томограммы.
|
|