оглавление ДМ экономическая информатика визуальные среды - 4GL Теория и практика обработки информации

Точность и количество реализаций модели при определении средних значений параметров

Найдем функциональную связь точности е и достоверности а с количеством реализаций модели, когда в качестве показателей эффективности выступают матожидание и дисперсия некоторой случайной величины (времени, расстояния и т. п.).

Определение оценки матожидания

Найдем искомую связь для случая, когда целью эксперимента является определение оценки матожидания некоторой случайной величины.

В прогонах модели получены независимые значения интересующего нас показателя эффективности:

В качестве оценки матожидания возьмем выборочное среднее (среднее арифметическое):

В последующей теме мы покажем, что оценка такого вида является наилучшей.

Согласно центральной предельной теореме, если значения независимы и имеют конечные дисперсии одного порядка, то при большом числе слагаемых случайная величина имеет практически нормальное распределение с матожиданием и дисперсией соответственно:

где - дисперсия искомой случайной величины

Следовательно, справедливо

где - интеграл вероятности.

В некоторых изданиях под интегралом вероятности понимают несколько иное выражение, поэтому целесообразно пользоваться интегралом Лапласа, который связан с интегралом вероятности

так: . - интеграл Лапласа. Из приведенного следует:

Сравнивая это выражение с выражением (4.1), имеем:

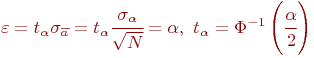
Интеграл Лапласа табулирован, следовательно, задаваясь значением достоверности , определяется аргумент .

Итак, искомая связь между точностью , достоверностью и числом реализаций модели получена:

Из выражений (4.2) следует:

увеличение точности на порядок (уменьшение ошибки на порядок) потребует увеличения числа реализаций на два порядка;
число необходимых реализаций модели не зависит от величины искомого параметра а от дисперсии

Достоверность результата указана значением аргумента функции Лапласа . Связь значения с находится из таблицы значений функции (интеграла) Лапласа. Наиболее употребительные соответствия и приведены в табл. 4.3.

Таблица 4.3. Фрагмент таблицы функции (интеграла) Лапласа
	0.8	0.85	0.9	0.95	0.99	0.995	0.999
	1.28	1.44	1.65	1.96	2.58	2.81	3.30

Чтобы пользоваться формулами (4.2), нужно знать дисперсию . Очень редки случаи, когда значение дисперсии известно до эксперимента, поэтому возможны два способа предварительного определения дисперсии.

Первый способ. Иногда заранее известен размах значений искомой случайной величины:

В предположении нормального распределения случайной величины , можно с использованием "правила трех сигм" получить приближенную оценку :

Второй способ. Надо воспользоваться оценкой дисперсии. Для этого необходимо выполнить предварительный прогон модели в количестве реализаций. С использованием полученного ряда , найдем оценку дисперсии:

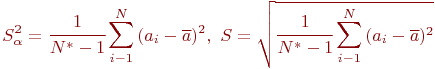
Здесь - среднеарифметическое значение по измерениям. И в этом случае формулы (4.2) имеют вид:

Вычисленную дисперсию подставим в формулу для определения . Если окажется то моделирование должно быть продолжено до выполнения реализаций. Если же , то моделирование заканчивается. Необходимая точность оценки случайной величины (искомого показателя эффективности) при заданной достоверности достигнута.

Если в технических условиях задана относительная точность , то формулы (4.3) принимают вид:

Значение определяется на основании прогонов модели. Все дальнейшие расчеты аналогичны только что рассмотренным аналитическим выражениям.

Вышеприведенные рассуждения и выражения были справедливы в предположении нормального закона распределения случайной величины . Если в этом есть сомнение, то для определения связи , и можно воспользоваться неравенством Чебышева П. Ф.:

С учетом направления знаков неравенств получим:

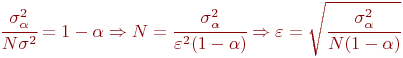
Также как и в предыдущих случаях вместо неизвестной дисперсии следует использовать ее оценку , вычисленную по данным прогонов модели. И еще: обратим внимание, что в данном случае достоверность участвует в формулах в явном виде.

Итак, в выражениях (4.3) мы вместо неизвестной дисперсии используем ее оценку . В этом случае вместо аргумента функции Лапласа надо использовать параметр распределения Стьюдента , значения которого зависят не только от уровня достоверности , но и от числа так называемых степеней свободы . Здесь, как и прежде, - число прогонов модели. Вообще-то, при распределение Стьюдента стремится к нормальному распределению, но при малом числе прогонов модели заметно отличается от .

Для практических целей значения можно взять из табл. 4.4.

Из табл. 4.4 видно, что при значения и практически совпадают. Но при меньших значениях следует пользоваться величиной .

Таблица 4.4. Таблица значений t_{a}

	0.8	0.9	0.95	0.99	0.999
10	1.37	1.81	2.23	3.17	4.6
20	1.33	1.73	2.1	2.85	3.73
30	1.31	1.7	2.04	2.75	3.65
40	1.3	1.68	2.02	2.7	3.55
60	1.3	1.67	2.0	2.67	3.41
120	1.29	1.66	1.98	2.62	3.37

Определение оценки дисперсии

Мы научились находить оценку матожидания некоторой случайной величины с заданными точностью и достоверностью.

Теперь рассмотрим задачу определения оценки дисперсии случайной величины также с заданными точностью и достоверностью.

Опустим вывод и приведем окончательный вид формул для расчета и :

где - эмпирический центральный момент четвертого порядка:

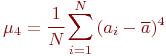
Неизвестное значение заменяется оценкой , как было рассмотрено ранее.

Если определяемая случайная величина имеет нормальное распределение, то и выражения для и принимают вид:

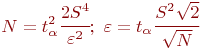
Как и ранее при малых значениях ( ) следует использовать параметр распределения Стьюдента .

Из сопоставления (4.3) и (4.4) следует, что одно и то же количество реализаций модели обеспечит разное значение ошибки при оценке матожидания случайной величины и ее дисперсии - при одинаковой достоверности. И иначе: одинаковую точность определения оценок матожидания и дисперсии случайного параметра при одинаковой достоверности обеспечит разное число реализаций модели.

Пример 4.5. В результате предварительных прогонов модели определена оценка дисперсии .

Определить число реализаций модели и для определения оценок матожидания и дисперсии случайной величины соответственно с точностью и достоверностью

Решение

Ссылки

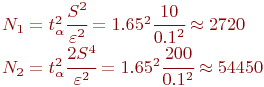
Боев В.Д., Сыпченко Р.П. Компьютерное моделирование

оглавление ДМ экономическая информатика визуальные среды - 4GL Теория и практика обработки информации

Знаете ли Вы, что экономико-математическое моделирование - это концентрированное выражение наиболее существенных взаимосвязей и закономерностей поведения управляемой системы в математической форме (В.С. Немчинов).

НОВОСТИ ФОРУМА

Рыцари теории эфира