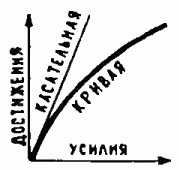
Рис. 1. В законе «Достижения пропорциональны усилиям» отражается фундаментальный принцип математического анализа: всякая гладкая функция в малом (то есть при малых приращениях аргумента) приближенно линейна.
Наука и жизнь, 1989, № 10
С недавних пор термин «катастрофа» начал встречаться не только в газетных текстах, но и в той науке, которую принято считать самой абстрактной из всех,- в математике. Ну а то, какой степени абстракции достигла современная математика, можно продемонстрировать следующим примером: вместо высказывания «Петя вымыл руки» нынешние математики говорят весьма просто - существует такое t1<0, что образ точки t1 при отображении t--> Петя (t) принадлежит множеству грязноруких, и такое t2, что t1<t2<=0 и образ точки t2 при указанном выше отображении принадлежит дополнению к описанному множеству. Но если математики теперь изъясняются на столь эзотерическом языке, то какой смысл они вкладывают в понятие катастрофы? О том, что такое математическая теория катастроф, рассказывает одни из крупнейших математиков современности, член-корреспондент Академии наук СССР Владимир Игоревич АРНОЛЬД.
Сначала мысль, воплощена
В поэму сжатую поэта,
Как дева юная, темна
Для невнимательного света;
Потом, осмелившись, она
Уже увертлива, речиста,
Со всех сторон своих видна.
Как искушенная жена
В свободной прозе романиста;
Болтунья старая, затем
Она, подъемля крик начальный.
Плодит в полемике журнальной
Давно уж ведомое всем.Е. Баратынский
Первые сведения о теории катастроф появились в начале 70-х годов. В массовых журналах типа «Тайм» и «Ньюсуик» сообщалось о перевороте в математике, сравнимом разве что с изобретением Ньютоном интегрального и дифференциального исчисления. Журналисты вдохновенно писали, что новая наука - теория катастроф - для человечества гораздо ценнее, чем классический математический анализ: в то время как ньютоновская теория позволяет исследовать лишь плавные, непрерывные процессы, теория катастроф дает универсальный рецепт для исследования всех скачкообразных переходов, разрывов и внезапных качественных изменений. Появились сотни научных и околонаучных публикаций, в которых теория катастроф применялась, например, к эмбриологии, кардиологии, психологии, лингвистике, экономике, социологии и геологии, не говоря уже о таких «естественных» дисциплинах, как оптика, теория устойчивости упругих конструкций и кораблей при волнении или, например, теория элементарных частиц. Среди публикаций по теории катастроф есть самые экзотические, в частности о психических расстройствах и восстаниях заключённых, о поведении биржевых игроков и влиянии алкоголя на водителей и даже о цензуре на эротическую литературу.
Маяковский заметил как-то, что сущность математики не в том, какие предметы она исследует, а в том, какие законы обнаруживает. Человек, открывший, что дважды два четыре, говорил он, был великим математиком, даже если он открыл это, считая окурки. Тот, кто теперь считает по той же формуле паровозы,- вообще не математик.
В прошлом веке математику делили на чистую - равно применимую к окуркам и паровозам - и прикладную, то есть специально приспособленную к паровозам. А сравнительно недавно, когда потребовалось перейти от паровозов к атомам, самолётам и спутникам, вдруг оказалось, что чистая - «окурочиая» - математика с её необычными объектами, такими, как представления групп, комплексные многообразия, многомерные пространства, и довольно-таки отвлечёнными разделами вроде топологии или функционального анализа гораздо лучше приспособлена к новым задачам, чем созданная для чисто практических нужд «паровозная».
А какова же по этой классификации теория катастроф, к чему она ближе, к чистой математике или прикладной?
|
Рис. 1. В законе «Достижения пропорциональны усилиям» отражается фундаментальный принцип математического анализа: всякая гладкая функция в малом (то есть при малых приращениях аргумента) приближенно линейна. |
Оказывается, что математическим источником теории катастроф служит сравнительно молодой раздел чистой, «настоящей» математики, который называется теорией особенностей гладких отображений. Фактически теория особенностей - смелое обобщение исследования функций на максимумы и минимумы. Почему такое исследование необходимо? Дело в том, что минимумы и максимумы представляют собой критические точки функции, которые во многом определяют её поведение. Известный французский математик Поль Монтель выразил это так: «Функции, как и живые существа, характеризуются своими особенностями». А чтобы понять, как именно, нам придётся рассмотреть несколько типичных примеров.
Современник Ньютона, английский учёный Гук, установил следующий закон, справедливый для упругих тел: удлинение такого тела, например, обычной пружины, почти пропорционально приложенной силе, пока она мала. (Это утверждение впоследствии так и назвали - законом Гука.) Точно так же в нормальных рыночных экономических условиях приращение спроса пропорционально малому уменьшению цены. И вообще очень часто достигаемый эффект оказывается пропорциональным затраченным усилиям. Однако нужно иметь в виду, что это верно лишь при малых приращениях, как часто говорят, локально (скажем, нынешнее уменьшение потребления алкоголя вряд ли пропорционально повышению цены на водку).
Приведенные примеры отражают один из универсальных законов:
I. В окрестности некритической точки приращение функции почти пропорционально приращению аргумента. Фактически этот закон отражает основной принцип классического математического анализа - всякая гладкая, то есть не имеющая изломов и «клювиков», функция на малых участках (как говорят, в малом) приближенно линейна. Иными словами, гладкую кривую можно заменить её касательной (рис. 1). С простейшими универсальными законами такого рода мы встречаемся столь часто, что уже перестали им удивляться. Но как прийти к пониманию этих законов, «прочувствовать» их? Так вот, оказывается, что исследование зависимости всевозможных математических объектов от определяющих их параметров и приводит к универсальным законам. Именно в этом, по существу, основной вывод математической теории особенностей.
|
Рис. 2. Универсальный закон квадратичности: в окрестности точек максимума или минимума приращения функции (соответственно отрицательное или положительное) приблизительно пропорционально квадрату приращения аргумента. Вдобавок типичная кривая переходит в точке касания с одной стороны аппроксимирующей её параболы на другую. |
Если рассматривать функцию не локально, то есть не на малом участке, а в целом, то она может быть и сильно нелинейной, например, иметь максимумы и минимумы. В окрестности точки максимума или минимума график типичной функции можно приближенно заменить параболой (рис. 2). Отсюда следует универсальный закон:
II. В окрестности максимума (минимума) приращение типичной функции почти пропорционально квадрату приращения аргумента.
В частности, небольшое отклонение аргумента от его оптимального значения практически не сказывается на значении функции. Например, малый поворот двигателей реактивного самолета (рис. 3) практически не меняет результирующую силу тяги, но спасает от реактивной струи хвостовое оперение. Действительно, потеря тяги пропорциональна квадрату малого угла поворота, то есть оказывается, как принято говорить, величиной более высокого порядка малости по сравнению с отклонением струи, которое пропорционально величине самого угла. Другой пример: с приближением к оптимальному состоянию затрачиваемые усилия перестают сказываться на достижениях.
Третий универсальный закон можно сформулировать так:
III. Типичная плоская кривая касается прямой не более, чем в двух точках.
Действительно, от касания в трёх точках можно избавиться малым изменением формы кривой (рис. 4), касание же в двух точках устойчиво, то есть не исчезает при малом шевелении кривой. Правда, чтобы сохранить касания в двух точках, придётся пошевелить и саму касательную. Третий универсальный закон имеет фундаментальное значение в теории оптимизации (см. рис. 5).
Универсальные законы, которым подчиняются более сложные системы (описываемые многими функциями многих переменных), уже не столь очевидны. Вот один из примеров:
IV. Типичная поверхность не касается никакой прямой более чем в четырёх точках.
В этом можно убедиться после некоторого экспериментирования с картофелинами и карандашом. Эксперимент показывает также, что касание в 4 точках устойчиво.
Во всех рассмотренных ситуациях речь идет об универсальных законах, которые выполняются для любых гладких объектов (функций, кривых, поверхностей), за исключением лишь некоторых специальных, «нетипичных». Интересно, что такие, казалось бы, простые объекты, как плоскость и цилиндр,- нетипичные поверхности.
Теперь мы, пожалуй, уже готовы к тому, чтобы понять, что имеют в виду математики, произнося слово «катастрофа». Правда, вначале нам придется сделать еще одно небольшое математическое усилие. Представим себе кубическую зависимость - функцию у = х3 (рис. 6). В нуле она имеет «нетипичную» кубическую особенность. Но если задана не индивидуальная функция, а целое семейство функций, зависящих ещё от некоторого параметра, то оказывается, что существует такое значение параметра, при котором кубическая особенность становится устойчивой. Слово «устойчивость» здесь означает, что во всяком близком семействе при некотором близком значении параметра встретится точно такая же особенность.
Универсальный пример такого семейства- множество кубических функций у = х3+рх переменной х, зависящих к тому же от параметра р. Вид графика таких функций при разных значениях параметра показан на рис. 7.
Пока параметр р отрицателен, функция имеет вблизи нуля локальные максимум и минимум. Когда параметр р стремится к нулю, максимум и минимум сближаются, и при нулевом значении параметра возникает кубическая особенность. При положительных значениях параметра и максимум, и минимум исчезают, «убив» друг друга. Все эти явления универсальны и устойчивы, они наблюдаются и в семействах, близких к рассматриваемому. Поэтому такие явления имеют широкую область применимости.
|
Рис. 3. Как спасти хвостовое оперение реактивного самолета от струи раскаленных газов? Небольшое отклонение значения аргумента от оптимального практически не сказывается на значении функции. В частности, малый поворот реактивных двигателей не меняет результирующую силу тяги. |
Пусть, например, наша функция характеризует состояние экономики (скажем, величину дохода правящего класса) в зависимости от какого-либо параметра. (В качестве такого параметра можно взять, к примеру, предприимчивость населения или гласность принятия решений, или правдивость печати.) Если экономика регулируется так, чтобы обеспечивать максимизацию функции, то система будет находиться в точке максимума. А до тех пор, пока с изменением дополнительного параметра этот максимум - локальный оптимум - не исчезнет.
В этот момент система будет вынуждена скачком перейти в далекое от исходного состояние В (рис. 8). Такого рода перескоки и получили название катастроф, так как они связаны с резкими изменениями в состоянии системы и могут приводить к её разрушению.
Если бы мы не ограничивались узкими рамками малых изменений вблизи рассматриваемого локального оптимума, то картина могла бы быть, например, такой. Вначале оптимальное решение единственно (А на рис. 9). По мере развития системы возникает побочный максимум В - новый локально-оптимальный, но вообще-то не наилучший режим. Он рождается вместе с близким локальным минимумом. Кстати, это явление рождения двух экстремумов описывается таким же универсальным законом, как и изображённое на рис. 7 их взаимное уничтожение, меняется только направление изменения параметра. Далее, побочный максимум обгоняет исходный (С). Начиная с этого момента, новый режим уже выгоднее старого. Но переход на него затруднён необходимостью резкого перескока - катастрофы. Отсюда вытекает правило:
V. При плавном переходе от одного локально-оптимального режима к другому необходимо временное ухудшение.
|
Рис. 4. Типичная кривая не имеет тройных касательных. При этом касание в двух точках устойчиво» то есть не исчезает при малом шевелении кривой. |
|
Рис. 5. Выбор пульсирующего оптимального режима. Предположим, что зависимость скорости выпуска продукции каким-либо производством (например, мельницей) от скорости подачи сырья изображается невыпуклой кривой. Как организовать работу, чтобы суммарный выход продукции при заданной средней скорости С подачи сырья (то есть при заданном расходе сырья за большое время) был максимальным? |
Оказывается, оптимальный режим - пульсирующий: он составляется из чередующихся периодов интенсивной загрузки сырья (точка А) и слабой загрузки (точка В). Действительно, требуется так распределить массы по кривой, изображённой на рисунке, чтобы центр тяжести лежал над точкой С и находился возможно выше. Такое распределение масс сосредоточено в двух точках А и В касания кривой с прямой.
Оптимальный режим составляется из смеси двух, а не большего числа режимов, именно потому, что прямая касается типичной кривой не более чем в двух точках (см. рис. 4.).
|
Рис. 6. График функции у=х3. Эта функция имеет при х=0 нетипичную, кубическую особенность. |
|
Рис. 7. Универсальная деформация кубической особенности. При возрастании параметра максимум и минимум функции сближаются и в конце концов исчезают, «убив» друг друга. |
В линейных системах малое изменение параметра в сторону лучшего режима улучшает положение. В отличие от этого, после достижения локального оптимума малые изменения управляющего параметра, направленные в сторону лучшего режима, не улучшают, а ухудшают положение. И если, как это обычно бывает, система сама стремится локально оптимизировать своё состояние, то она будет отвечать на недостаточно радикальные изменения возникновением сильных тенденций возврата к старому режиму. Этим, думается, можно объяснить неудачу многих реформ, в частности экономических.
В живой природе аналогичная трудность, например, необходимость полной перестройки организма гусеницы для образования бабочки преодолевается при помощи специальной стадии - куколки. В этом случае отжившая система (гусеница) сама создаёт в своих недрах новую систему, которая впоследствии уничтожает старую (куколка в конце питается остатками гусеницы).
Наконец, в ходе дальнейшего развития системы исходное локально-оптимальное состояние вообще исчезает (D) и переход на далёкий от первоначального режим становится неизбежным (Е).
Универсальный закон (рис. 7) приводит к выводу:
VI. Расстояние от исчезающего локально-оптимального режима до движущегося ему навстречу локально-минимального - порядка квадратного корня из отличия параметра от катастрофического значения. Поэтому в момент катастрофы оба режима сближаются с бесконечной скоростью. Это, кстати, объясняет, почему так трудно бороться с грозящей катастрофой, когда её признаки сделались уже заметными.
Описанный сценарий оказывается лишь одной из возможных последовательностей локальных метаморфоз, качественных перестроек, или, как выражаются математики, бифуркаций. Все возможные сценарии взаимодействия двух локально-оптимальных режимов даются, как выяснилось, универсальным законом
|
Рис. 8. Катастрофическое изменение режима. Модели, основанные на представлениях теории катастроф» некоторые авторы пробуют применять и социальным системам и экономке. |
|
Рис. 9. Сценарий глобальных перестроек в развивающейся системе. При плановом переходе от одного локально-оптимального режима к другому необходимо временное ухудшение. |
у = х4 + ах2 + bх
с параметрами a и b. На рис. 10 изображён график экстремального значения у как функции параметров a и b.
Сценарий, описанный выше, изображается на этом графике путём I, заканчивающимся катастрофическим скачком. Однако к той же самой конечной цели можно прийти без катастрофы, даже зайдя уже достаточно далеко по катастрофическому пути. Для этого надо вернуться назад и обойти разделяющую конкурирующие режимы точку с другой стороны (путь II).
Поверхность, изображенная на рис. 10, называется «ласточкиным хвостом». Она постоянно встречается в теории особенностей в качестве универсальной модели. Например, такие же «ласточкины хвосты» имеют фронты типичных воли, распространяющихся в трёхмерном пространстве. В местах особенностей волны особенно сильны. Именно этими особенностями объясняются, в частности, радуга на небе и разрушительная ударная волна от сверхзвукового самолёта.
Универсальных законов, подобных приведённым выше, оказалось не так уж много (хотя число их, конечно, растёт с увеличением числа переменных и параметров). Кроме ласточкиного хвоста в трёхмерном пространстве, особенно часто встречается еще зонтик Уитни-Кэли (рис. 11) - поверхность, заданная уравнением у2 = zx2. Зонтиком эта поверхность называется потому, что, кроме нарисованной на рис. 11 поверхности, выписанному уравнению удовлетворяет и отрицательная часть оси z - своего рода «ручка» зонтика.
|
Рис. 10. Ласточкин хвост: универсальный закон зависимости оптимальных значений от параметров.
Рис. 11. Зонтик Уитни - Кэли. Зонтиком эта поверхность называется потому, что уравнению, задающему поверхность, удовлетворяет и отрицательная часть оси Z - своего рода «ручка» зонтика.
Рис. 12. Сборка Уитни: универсальный закон, в соответствии с которым изменяется внутреннее состояние системы в зависимости от параметров.
Рис. 13. Особенность, называемая складкой, возникает, в частности, при проектировании сферы на плоскость в точках экватора.
Рис. 14. Экспериментальное наблюдение сборки Уитни. На поверхности бутылки можно увидеть две сборки. Они устойчивы, в чём можно убедиться, покачивал бутылку. |
Если объекты нашего исследования характеризуются двумя параметрами, а мы, не зная их, измеряем три характеристики объекта и изображаем результат измерений точкой трехмерного пространства, то полученные точки расположатся на некоторой поверхности. И вот оказывается, что, несмотря на полную гладкость зависимости измеряемых характеристик от параметров объекта, получающаяся поверхность, вообще говоря, имеет особенности, а именно зонтики, локально устроенные так, как указано на рис. 11.
Характерная особенность образуется при проектировании гладкой поверхности общего положения на плоскость.
Если соединить графики функций рис. 7 в одну поверхность (рис. 12) и спроектировать эту поверхность на плоскость (p, y) вдоль оси х, то видимый контур поверхности будет иметь остриё (точки возврата). На самой поверхности в этом месте нет никакой особенности. Особенность имеет лишь проектирование. При изменении направления проектирования особенность перемещается по поверхности. Эта особенность называется «сборкой Уитни».
В 1955 году американский математик Хасслер Уитни опубликовал работу «Об отображениях плоскости на плоскость». Фактически именно эта работа и заложила основу теории особенностей гладких отображений, а с нею и теории катастроф. Отображение поверхности на плоскость - это сопоставление каждой точке поверхности точки плоскости. Уитни заметил, что в случаях «общего положения», то есть во всех случаях, кроме некоторых исключительных, встречаются особенности лишь двух видов - все другие разрушаются при малом «шевелении» тел или направлений проектирования, тогда как эти два вида особенностей устойчивы и сохраняются при малых деформациях отображения.
Сборка - одна из таких особенностей, вторую особенность Уитни назвал складкой, она возникает, если проектировать сферу на плоскость в точках экватора (рис. 13). Две сборки можно увидеть на поверхности бутылки (предпочтительнее из-под молока, рис. 14). Покачивая бутылку, мы экспериментально убеждаемся в том, что сборка устойчива. И вообще, отображения гладких поверхностей на плоскость окружают нас со всех сторон. Действительно, большинство окружающих нас тел ограничено гладкими поверхностями, при этом видимые контуры тел - проекции поверхностей, ограничивающих тела, на сетчатку глаза. Приглядываясь к окружающим нас телам, например, к лицам людей, мы можем изучить особенности видимых контуров. Например, точки сборки можно увидеть в чертах окружающих нас лиц там, где линия контура «исчезает» (рис. 15). Если применительно к человеческим лицам говорить на геометрическом языке, то можно заметить, что линия контура имеет касательную вплоть до точки сборки, но с приближением к этой точке кривизна линии растет до бесконечности.
Теорема Уитни стала прообразом многочисленных универсальных законов строения особенностей, открытых в последующие годы. Простейшие из этих законов были уже известны в конкретных примерах специалистам в соответствующих областях. Историки науки недавно подметили, что до появления теории особенностей открытия этого рода особенно часто встречались в работах, удостоенных Нобелевской премии. Положение здесь такое же, как с математическим анализом: Гюйгенс решал без его помощи практически все задачи, решаемые Ньютоном и Лейбницем с помощью анализа, но для этого нужно было иметь гений Гюйгенса. Теперь же такие задачи благодаря анализу легко решает любой студент. Точно так же теория особенностей сделала легкодоступным тонкое искусство построения правильных моделей явлений, когда отбрасываются большие, но «физически несущественные» величины и сохраняются меньшие, но «физически важные» члены.
|
Рис. 15. Складии и сборки на лице Мики Морозова (портрет Валентина Серова). |
Из предшественников теории особенностей упомяну Гюйгенса (теория эволют и эвольвент), Гамильтона (теория систем лучей), Кэли (зонтики, фронты и каустики), Пуанкаре (теория бифуркаций, включая - катастрофисты обычно этого не знают - построение «версальных деформаций»), А. А. Андронова (структурная устойчивость, бифуркации аттракторов), Максвелла (фазовые переходы), Гиббса (правило фаз), Н. Н. Семёнова (тепловой взрыв), Я. Б. Зельдовича (теория горения и космология), Пирси (волновая оптика), Койтера (теория упругости), Л. Д. Ландау (фазовые переходы второго рода) и т. д.
Понимание того, что в основе всех этих (и многих других) исследований лежит одна и та же математическая структура, пришло не сразу, но когда это было осознано, то прогресс в каждой из перечисленных областей начал немедленно приводить к продвижениям во всех остальных. В настоящее время теория особенностей, бифуркаций и катастроф - один из наиболее бурно развивающихся отделов математики.
Термин «катастрофа» был введён в конце 60-х годов французским математиком Р. Томом для обозначения качественного изменения объекта при плавном изменении параметров, от которых объект зависит. Этот термин, призванный заменить использовавшиеся до него термины «бифуркация», «перестройка», «метаморфоза», завоевал широкую известность после того, как в начале 70-х годов английский тополог К. Зиман предложил употребить название «теория катастроф» для соединения теории особенностей, теории бифуркаций и их приложений.
Математику трудно согласиться с тем, что введение нового термина, не сопровождаемое открытием новых фактов, представляет собой значительное достижение. Однако успех «кибернетики», «странных аттракторов», «синергетики» и «теории катастроф» показывает плодотворность словотворчества как метода научной работы. Этот метод, впрочем, известен давно, и Пуанкаре употреблял его уже вполне сознательно.
«Трудно поверить,- говорил он,- какую огромную экономию мысли может осуществить одно хорошо подобранное слово. Часто достаточно изобрести одно новое слово, н это слово становится творцом». Более того, согласно Пуанкаре «математика-это искусство давать одно и то же название различным вещам». «Факт... приобретает свое значение лишь с того дня, когда более проницательный мыслитель подметит сходство, которое он извлечет на свет и символически обозначит тем или иным термином» (все 4 фразы - из «Науки и метода», глава «Будущее математики», стр. 296-301 в книге А. Пуанкаре «О науке», М., 1983). Однако Ньютон, сравнивая математику с теорией типа теории катастроф, писал: «Математики, которые всё открывают и устанавливают и проделывают всю работу, должны довольствоваться ролью сухих вычислителей и чернорабочих. Другой (катастрофист.- В. А.), который всего лишь все схватывает и на всё претендует, присваивает себе всё изобретения как своих последователей, так и предшественников».
При практическом применении теории особенностей и теории катастроф мы встречаемся с такими же трудностями, которыми всегда сопровождаются применения математики. Нет сомнения, что арифметика полезна: умножать и складывать лучше, чем отнимать и делить. Однако даже самое безупречное умножение чисел само по себе еще недостаточно. (С аналогичной трудностью столкнулся Буратиио, когда решал предложенную ему Мальвиной арифметическую задачу. Затруднение вызвала не арифметика, а более важная проблема: «Зачем я отдал некту два яблока?!»)
Таблица умножения полезна для бухгалтерского учета, но не предохраняет от хищений социалистической собственности. Точно так же знание универсальных законов, по которым происходят катастрофы, само по себе ещё не предохраняет от них. И без теории ясно, что несоблюдение техники безопасности, а также падение уровня компетентности специалистов неизбежно повышает вероятность катастроф. Там, где разорвана обратная связь в системе управления, где ответственные решения принимаются лицами или организациями, не несущими материальной ответственности за их последствия («стрелочник виноват»), катастрофы становятся неизбежными, что и наблюдается, к сожалению.
|
Рис. 16. Метаморфоза Н4 на волновом фронте. При распространении воли первоначально гладкий волновой фронт перестраивается и приобретает сложные особенности. Здесь изображена одна из типичных метаморфоз уже особого волнового фронта, огибающего гладкое препятствие в трёхмерном пространстве. Такая перестройка волнового фронта возникает в некотором отдалении от поверхности препятствия. Исследование этой метаморфозы волнового фронта основано на геометрии правильного 600-гранника в четырёхмерном пространстве. Более простая особенность, обозначенная на рисунке Н3, соответствует обычному икосаэдру (правильному двадцатиграннику в трёхмерном пространстве), особое ребро возврата Н2 правильному пятиугольнику на плоскости. |
«Шахта становится слишком глубока,- писал о математике в 1781 году Лагранж Даламберу,- и, если не будут найдены новые жилы, придется совсем её забросить,., иначе места по математике в Академии станут тем, чем уже стали кафедры арабского языка в университете».
Сомнения в полезности математики высказывал и Маяковский («Гимн учёному»):
...И ему не нудно,
что растёт человек глуп и покорен.
Ведь зато он может
ежесекундно
извлекать квадратный корень.
В такой репутации своей науки отчасти виноваты сами математики, «складывающие простые числа, вместо того, чтобы их умножать», как говорил Л. Д. Ландау.
Правда, последнее десятилетне знаменуется крутым поворотом современной математической науки от абстрактно - аксноматических исследований к естествознанию (это проявилось даже в тематике такого форума абстрактной математики, как знаменитый семинар Бурбаки). Теория особенностей - одна из тех жил, о которых говорил Лагранж, и одна из самых живых ветвей современной математики, где её наиболее абстрактные отделы (алгебраическая геометрия, теория групп отражений, теория алгебр Ли) соединяются с самими прикладными (теория динамических систем, геометрическая и физическая оптика, оптимизация и теория управления).
На рис. 16 изображена одна из типичных и устойчивых метаморфоз распространяющегося волнового фронта в задаче об обходе препятствия в трёхмерном пространстве (этот результат был получен в 1984 году советским математиком О. П. Щербаком). Задача относится к теории оптимального управления, решение же её оказывается связанным (довольно таинственным образом) с «калейдоскопом Н4» - правильным 600-гранником в четырёхмерном пространстве. И именно теория таких многогранников (давно построенная в «абстрактной» математике) позволила разобраться в сложных перестройках фронта, изображённых на рис. 16.
В подобных неожиданных проявлениях загадочного единства всего сущего - особая притягательность теории особенностей, да и вообще математики. Как сказал поэт:
Мир создан купно. Целостность его
Не устает показывать планета.
И вот в глаза бросается родство
То тут, то там сияющего света.
Наверно, есть какое-то ядро,
Откуда свет расходится повсюду:
И в зрелый цвет сентябрьских щедрот,
И в нашей жизни трепетное чудо...
Член-корреспондент АН СССР В. АРНОЛЬД
|
|