
УМОВ Николай Алексеевич
ЗАКОНЫ КОЛЕБАНИИ В НЕОГРАНИЧЕННОЙ СРЕДЕ ПОСТОЯННОЙ УПРУГОСТИ
Впервые напечатано в Математическом сборнике, т. 5, 1870 г. (Прим. ред.)
§ 5. Мы переходим к исследованию изотермических
поверхностей. Предположим, что поверхность волны есть поверхность изотермическая и p — её термометрический
параметр. Означая через
ренциалъныи параметр второго порядка функции р
/; имеем: А2р = 0, так как p есть параметр термометрический. Следовательно,
откуда
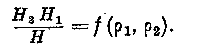
Вставляя в это выражение величины //,, 7/
: из уравнений (12), находим:
Это выражение должно существовать для всяких р, рь р
2. Мы можем удовлетворить ему при двух предположениях :
! g
постоянное.Рассмотрим первое предположение. Мы находим:

Предполагая, что
P и Q ые обращаются в нуль, мы находим из двух последних уравнений:Pl = 0, Q, = 0.
Следовательно, рассматриваемая поверхность есть сфера. Величина //, выраженная термометрическим параметром, б\'пет:

Если же мы примем Т
3 —0, то должны будем принять или JP1 = 0, то-есть Н1 = 0, что невозможно, или Q = 0, но тогда равенство P1Ql = 0 даёт или Рг == 0, или (>1 = 0, то-есть опять или Н1 = 0 или 7/2=0, что невозможно.Рассмотрим второе предположение. Оно влечёт за собою

Здесь возможны два случая:
Р=0,
q! 0 или Q = Q, />i=0.Примем последнее. Из уравнений (12) имеем:

Нг = Р^Нар,
ffa = Qi.Но
Elf // =
е я .Следовательно,
Bi~gPe>.;
Я2 = <?1-
Так как
Q=-0, /^ = 0, то из уравнений (14) находим: 9Р_ ___ n “5Q! __ л- — V/j n — • v/,
<??2 5?!
следовательно,
Обращаясь к уравнениям (7), мы находим следующие выражения для кривизны поверхностей р, р
1( р2:
Отсюда ясно, что рассматриваемая поверхность есть не что иное, как круглый цилиндр.
Итак, из всех изотермических поверхностей только плоскость, сфера и круглый цилиндр могут быть поверхностями волны.
|
|