 Корректирующее устройство можно
включить последовательно, параллельно-согласно или параллельно-встречно (по
схеме с обратной связью).
Корректирующее устройство можно
включить последовательно, параллельно-согласно или параллельно-встречно (по
схеме с обратной связью).В ТАУ можно выделить две характерные задачи: 1) в заданной САУ найти и оценить переходные процессы - это задача анализа САУ; 2) по заданным переходным процессам и основным показателям разработать САУ - это задача синтеза САУ.
Вторая задача сложнее в виду своей неоднозначности, многое определяется творческими способностями проектировщика. Поэтому обычно задачу синтеза САУ ставится ограниченно. Считается, что основная часть системы уже задана, что обычно имеет место. Требуется синтезировать корректирующие звенья, то есть выбрать их схему и параметры. При этом необходимо, чтобы в результате коррекции САУ обеспечивался требуемый запас устойчивости; точность управления в установившихся режимах и качество управления в динамических режимах.
14.1.1. Включение корректирующих устройств
 Корректирующее устройство можно
включить последовательно, параллельно-согласно или параллельно-встречно (по
схеме с обратной связью).
Корректирующее устройство можно
включить последовательно, параллельно-согласно или параллельно-встречно (по
схеме с обратной связью).
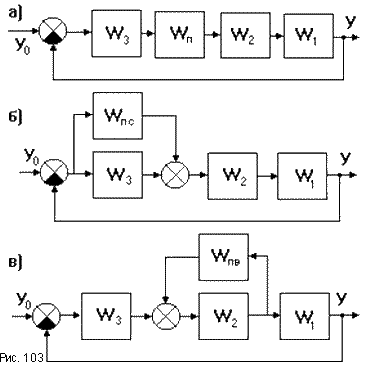
Последовательное корректирующее устройство с передаточной функцией Wп включается обычно после предварительного усилителя. На рис.103а предварительный усилитель имеет передаточную функцию W3, выходной каскад усилителя - W2, исполнительный элемент - W1.
Параллельно-согласное
корректирующее устройство с передаточной функцией Wпс (рис.103б) может
иногда при меньшей сложности обеспечить нужное преобразование сигнала. Например,
для коррекции свойств САУ часто требуются дифференцирующие и форсирующие звенья,
которые конструктивно очень сложны. В то же время параллельно-согласное включение
предварительного усилителя (W3 = K3)
и простого апериодического звена с передаточной функцией Wпс = 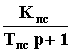 позволяет реализовать функцию
реального форсирующего звена. Такое соединение можно заменить эквивалентным форсирующим
звеном с передаточной функцией
позволяет реализовать функцию
реального форсирующего звена. Такое соединение можно заменить эквивалентным форсирующим
звеном с передаточной функцией
Wф
= W3 + Wпс =  ,
,
где
Tф1 = 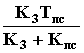 ; Tф2
= Tпс; Kф = K3
+ Kпс.
; Tф2
= Tпс; Kф = K3
+ Kпс.
Наибольшими возможностями в плане коррекции свойств САУ обладает корректирующее устройство с передаточной функцией Wпв, включенное по схеме с отрицательной или положительной обратной связью, охватывающей один из звеньев САУ, как правило исполнительный элемент или выходной каскад усилителя (усилитель мощности)(рис.103в). Такие обратные связи называются местными. При этом передаточная функция эквивалентного звена:
Wэкв
= 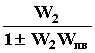 .
.
Обычно передаточную функцию выходного каскада усилителя W2 выбирают из условия |W2.Wпв| >> 1 в широком диапазоне частот, поэтому
Wэкв![]() 1/Wпв.
1/Wпв.
То есть свойства участка цепи с параллельно-встречным включением корректирующего устройства определяются только свойствами данного корректирующего устройства. Это основное достоинство данного способа включения. Влияние плохих свойств какого либо необходимого для САУ звена, например, его нелинейности, могут быть практически полностью устранены.
Местные корректирующие обратные связи делятся на жесткие и гибкие. Жесткая
обратная связь действует на систему как в переходном, так и в установившемся
режиме, то есть Wж(0)![]() 0.
Она реализуется безынерционным или инерционным звеном:
0.
Она реализуется безынерционным или инерционным звеном:
Wж
= Kж или Wж
= 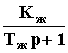 .
.
Гибкая обратная связь действует только в переходном режиме, она реализуется либо дифференцирующим, либо реальным дифференцирующим звеном:
Wг
= Kг pили Wг
=  .
.
Например, если интегрирующее звено Wи = Kи/p охвачено жесткой обратной связью звеном Wж = Kж, то
Wэкв
= 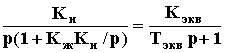 ,
,
где Kэкв = 1/Kж, Tэкв = 1/(Kи KэквKж). То есть жесткая обратная связь превращает интегрирующее звено в апериодическое. В случае гибкой обратной связи звеном Wг = Kгp получаем
Wэкв
= 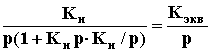 ,
,
где
Kэкв =  . То есть гибкая обратная связь
не изменяет структуру интегрирующего звена, но уменьшает его коэффициент передачи.
. То есть гибкая обратная связь
не изменяет структуру интегрирующего звена, но уменьшает его коэффициент передачи.
Таким образом, даже простейшие обратные связи способны существенно изменить свойства типовых динамических звеньев. Еще больший эффект дают сложные отрицательные и положительные обратные связи. Если основные элементы регулятора по своей природе позволяют создать обратную связь, то динамические свойства этих элементов часто могут быть изменены в нужном направлении.
14.1.2. Синтез корректирующих устройств.
Корректирующие устройства синтезируют на основании требований к свойствам САУ. Для этого необходимо знать передаточную функцию реальной САУ Wреал, которая чем то не удовлетворяет разработчика, и желаемую передаточную функцию Wжел , которой должна обладать САУ в результате корректировки ее свойств.
При синтезе корректирующих устройств сначала определяю передаточную функцию возможного последовательного корректирующего устройства исходя из соотношения: Wп = Wжел /Wреал. Затем выясняют, при каких передаточных функциях параллельно-согласного Wпс и параллельно-встречного Wпв корректирующих устройств будет получен тот же эффект. После этого решают, какое из них более целесообразно и проще создать. При этом исходя из рис.103 можно записать:
Wжел = W![]() Wп
= W1
Wп
= W1![]() W2.(W3
+ Wпс) = W
W2.(W3
+ Wпс) = W![]() (1
+ Wпс/W3) = W/(1 + W2
(1
+ Wпс/W3) = W/(1 + W2![]() Wпв),
Wпв),
где W = W1![]() W2
W2![]() W3.
Из этого соотношения можно определить формулы перехода от одного корректирующего
устройства к другому.
W3.
Из этого соотношения можно определить формулы перехода от одного корректирующего
устройства к другому.
14.2. Коррекция свойств САУ изменением параметров звеньев
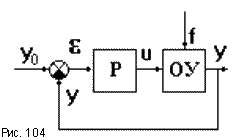 Рассмотрим примеры коррекции свойств
некоторой исходной замкнутой САУ (рис.104), передаточная функция которой в разомкнутом
состоянии:
Рассмотрим примеры коррекции свойств
некоторой исходной замкнутой САУ (рис.104), передаточная функция которой в разомкнутом
состоянии:
W(p) =  .
.
Для этого воспользуемся критерием Найквиста. Значения параметров звеньев в каждом конкретном случае будем оговаривать отдельно.
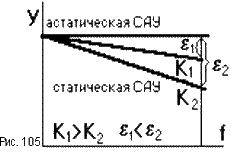
14.2.1. Изменение коэффициента передачи
Для увеличения точности статической САУ надо увеличивать коэффициент передачи K. С ростом K увеличивается жесткость статической характеристики САУ (рис.105), то есть уменьшается статическая ошибка e.
На рис.106 сплошными линиями показаны частотные характеристики исходной разомкнутой САУ при T1 = 0.5c, T2 = 0.02c, T3 = 0.002c, K = 10.
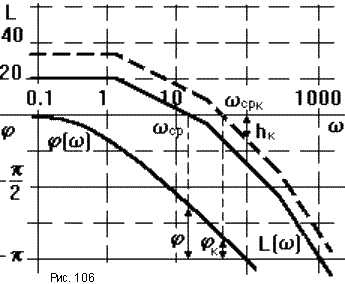
При увеличении коэффициента передачи
K в N раз ЛАЧХ, не меняя своей формы, поднимается вверх на 20lgN
(на рисунке изображена пунктирной линией). При этом ЛФЧХ остается без изменения.
Из рисунка видно, что с увеличением коэффициента передачи запас устойчивости
по модулю уменьшается с h![]() 30дб/дек
до hк
30дб/дек
до hк![]() 15дб/дек,
по фазе - с
15дб/дек,
по фазе - с ![]()
![]() 60o
до
60o
до ![]() к
к![]() 15o
.
15o
.
То есть, при повышении точности САУ путем увеличения коэффициента передачи необходимы мероприятия по повышению запаса устойчивости. Это главный недостаток такой коррекции.
К достоинствам можно отнести повышение быстродействия САУ, так как частота среза wср увеличивается, следовательно постоянная времени САУ - уменьшается.
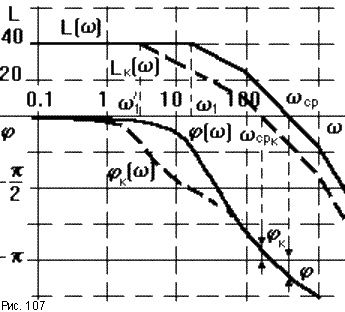
На рис.107 сплошными линиями изображены ЛЧХ разомкнутой САУ с параметрами:
T1 = 0.05c, T2
= 0.01c, T3 = 0.001c, K = 100.
Из рисунка видно, что САУ неустойчива. При увеличении постоянной времени T1
в 5 раз (T1’ = 0.2с) ЛАЧХ и ЛФЧХ приобретают
вид, показанный на рисунке пунктирной линией. При этом видим, что замкнутая
САУ становится устойчивой. Заметим, что сопрягающая частота W1
данного звена располагается левее частоты среза ![]() ср.
Если бы она располагалась правее частоты среза, то есть, если бы мы увеличивали
постоянную времени, например, третьего звена T3,
то это привело бы к уменьшению запаса устойчивости.
ср.
Если бы она располагалась правее частоты среза, то есть, если бы мы увеличивали
постоянную времени, например, третьего звена T3,
то это привело бы к уменьшению запаса устойчивости.
Частотные характеристики для этого случая приведены на рис.108.
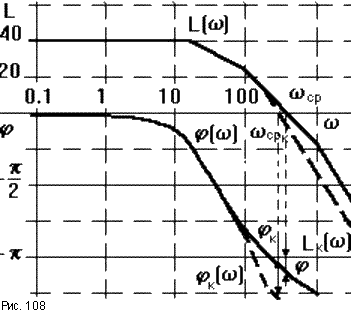
Аналогичное влияние оказывает постоянная времени колебательного звена. Влияние постоянной времени форсирующего звена обратное, то есть, если сопрягающая частота форсирующего звена располагается левее частоты среза, то увеличение его постоянной времени уменьшает запас устойчивости САУ, если правее, то запас устойчивости увеличивается.
Указанные зависимости справедливы лишь при условии, что сопрягающая частота расположена на некотором удалении (около одной декады) от частоты среза. Бывают и исключения из этого правила.
|
|