What is entropy in thermodynamics?

Q = U + pV,                                               (1)

Q must remain constant as the one of the components changes. In fact, in spontaneously occurring processes it decreases. Some of the energy is converted into some other thermodynamic function which Clausius called entropy (transformation in Greek). Equation (1) as amended by correction entropy has been called the second law of thermodynamics:

Q = U + pV-TS,                                                                  (2)

where T - absolute temperature, S - entropy.

With this approach, the entropy is given by:

S = q / T,                                                                      (3)

where q - reduced thermal energy. Equation (3) does not allow a quantitative calculation of the entropy due to the uncertainty the physical meaning of q. So widespread expression of entropy as a measure of the probability of the process:

S = klnW,                                                                       (4)

where k - Boltzmann constant, W - the probability of the process. It is a dimensionless quantity. To give this function the dimension of entropy, it is multiplied by a constant that has the dimension of entropy J / K. This makes the resulting value conditional and the carried out calculation formal, which does not reflect the physical essence of entropy.

The situation with the determination of the thermodynamic concept of entropy seems appropriate to characterize the statement of one of the leading experts on the subject [1]: "Thermodynamic definition of entropy often seems mysterious and arbitrary."

 Apparently, the physical content of the notion of entropy to be found in elementary energy acts (cycles) that occur in the interaction of atoms and molecules. This refers, for example, release or absorption of energy when the electron from one orbit to another or microgravity interaction of molecules and their complexes. Energy analysis of such interactions was made possible after the confirmation of the hypothesis P. Laplace "modification of gravitational forces into molecular ones with increasing density of matter" [2].

We are talking about the phenomenon of microgravity. Objects micron and nano sizes (atoms and molecules) having a density of ~ 10¹² g/cm³, interact in the inverse square law of gravity, but with an unusually large microgravity constant equal 1,847.10²⁸ сm³/gs². Using the laws of dynamics of orbital motion, which are derived from the law of gravity, it was possible to calculate the orbital distance, potential and kinetic energy and radiation energy in the interaction of objects specified dimensions. All this gets you closer to understanding the physical nature of the thermodynamic concept of entropy.

2. Entropy in the elementary energy cycle in the atom

Consider the energy conversion cycle "ionization - neutralization" in the case of a hydrogen atom. At the ionization the electron is transferred from the lower energy level to a higher one lying outside the atom. The potential energy is increased by the amount of ionization energy of 13.6 eV. The transition occurs with the energy level Ep = - 13.6 eV to zero potential energy. If you switch back from the energy level Ep = 0 to the lower level of Ep = -13.6 eV, which occurs spontaneously, in accordance with the virial theorem (5), half of the potential energy is used to increase the kinetic energy of the electron, and the second one to electromagnetic radiation:

Ep = 2Ek = Ek + Er                                                        (5)

Here Ep, Ek and Er potential, kinetic and energy of the radiation, respectively. We can assume that the problem of thermodynamic entropy is hidden in these transitions. If the released energy radiation is available for use, i.e., has not disappeared, the kinetic energy of the electron orbital motion caused by gravitational forces from the nucleus is lost to the outside observer. It can not be used and is more suited to role of the "disappeared" of energy, in other words the entropy.

In Table 1 below are detailed specification considered power cycle. In hydrogen atom selected three energy levels: the level of free electrons, which lies outside the surface of an atom at r> 110 pm, the level corresponding to the van der Waals radius of the atom r = 110 pm and the ionization level, located at r = 4,167 pm.

As mentioned above, the concept of microgravity [2] allows us to calculate the radii of atoms and bind them to the energy levels in an atom. Column 3 shows the reference values of the radiation frequency, which, in accordance with the original Bohr's theory is the frequency revolution of the electron on the orbit. Orbital radius of the electron calculated by the equation third Kepler law, which applied to the atom, has the form [3]:

ν = g^0,5m^0,5/2πr^1,5 ,                                                        (6)

where ν - frequency revolution on the orbit (radiation) s^-1, g - constant of microgravity equal 1,845.10²⁸ sm³/gs², m-proton mass 1,672.10^-24 g, r - orbital radius. For the ionization level and surface atom orbital radius respectively equal to 4.167 and 110.1 pm, see column 4.

Table 1. Parameters of the energy cycle in the hydrogen atom

Calculation of the potential energy Ep was carried out by the classical equation of potential energy in the orbital motion:

Ep = gm_em^p / r,                 (7)

where g - constant microgravity, me-electron mass equal 0,294.10-24 g [2], mp-proton mass 1,672.10^-24 g and r-orbital radius. The obtained values of the potential energy represented in column 7 of Table 1. The potential energy of the ionization level is -13.58 eV, surface of atom -0.51 eV, which practically coincides with the experimental (reference) data, which are, respectively, -13.60 and -0.38 eV.

Column 8 shows the results of the calculation of the kinetic energy for different energy levels. It was assumed that free electrons have zero kinetic energy of the orbital motion. Kinetic energy of the electron orbital motion in the surface layer and the ionization level is calculated by the orbital velocity (see column 5), which in turn is determined by the orbital velocity of the equation:

v_o = (gm_p / r) ^0,5,                                                                 (8)

where vo-orbital velocity, g-the constant microgravity, mp-proton mass, r-orbital radius

   Kinetic energy on the ionization level is 6.79 eV and 0.51 eV surface atom that in both cases is 0.5 Ep. Consequently, at both levels is performed with high accuracy, virial equation (5). The second half of Ep goes on radiation due to the intersection of the field lines.

The kinetic energy of the orbital motion of the electron in contrast to the energy of the radiation can not be used as the orbital motion are strictly defined parameters of the force center (gmp) according to equation (8). Basically, this energy is derived from the treatment, as it is located within an atom. Nevertheless, it is present in the system and the law of conservation of energy is conserved. The kinetic energy of the orbital moving electron immobilized by gravity core and is therefore "disappeared", i.e. entropy component of the total energy of the system.

The kinetic energy of the orbital revolution electron can be used if the electron orbital velocity increase due to the impact of external gravitational forces or radiation to the value of the parabolic velocity vp according to the equation:

v_p = (2gm_p/ r) ^0,5,                                                              (9)

To derive the electron outside the atom and overcome the forces of microgravity orbital velocity of the electron at the ionization level (r = 4,17 pm), it is necessary to raise the level of the parabolic velocity (1,217.10⁷ cm / s), see the column 6 in table1. In this case, the electron becomes "a free electron" and can be used to repeat the power cycle, or for any other purpose (electron conductivity, chemical reaction, etc.)

3. Entropy in the formation of a hydrogen molecule

As shown above, under the thermodynamic entropy should understand the orbital kinetic energy of the moving body, which "disappeared" as controlled power center, causing the orbital motion and is not available to an external observer. A similar situation is also observed in the interaction of two hydrogen atoms to form a diatomic molecule of hydrogen.

Hydrogen atoms have a radius of ~ 110 pm. When approaching the microgravity interaction of atoms occurs by their masses. According to the laws of the dynamics orbital motion the atoms come into orbital motion relative to each other by the type of binary stars A convergence of their nuclei take place, the potential energy decreases, there is emission of electromagnetic energy (heat of reaction), the kinetic energy of the orbital motion of the nuclei is increase and thus should be expected to increase entropy.

A schematic model of the hydrogen molecule, consisting of the two orbital rotating atoms about a common center of mass is presented in Figure 1. Protons (nuclei of atoms) (3) and (4) under the influence of microgravity are rotating on circular orbit (1). Orbital radius rc = 36 pm. Circulation of protons going around a common center of mass (2). Molecular radius rm = 146 pm. It summed up semi of the sum of the intermolecular distance and the radius of the hydrogen atom. The order of magnitude it is close to the experimental (reference) value equal to 124 pm. The direction of rotation indicated by the arrows of the protons

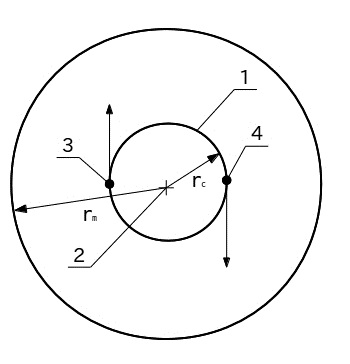
Fig.1. A schematic model of the hydrogen molecule: 1 - orbit motion of the protons, 2 - center of mass, 3 - and 4 - orbital moving protons, 5 - the border of the molecule.

Energy formation of molecule H2 previously discussed [4], where a change in the potential and kinetic energy. With a decrease in the interatomic distance from 157 to 71.2 pm according to equation (7) the potential energy decreases by 935 kJ / mol. Consequently, when such atoms approach taking into account equations (5) and (7) in the form of radiation may stand out 935/2 = 467.5 kJ / mol. This value is quite close to the experimental (reference) the binding energy of H-H 436 kJ / mol, which confirms the approach to the problem

As follows from equation (5) reduction of the interatomic distance with 157 pm to 71.2 also leads to an increase in kinetic energy of 0.5 Ep, that is 467.5 kJ / mol due to the increase of the orbital velocity of the protons. Such an increase in the kinetic energy of protons circulating confirmed by the coincidence estimated of the revolution frequency 0,1295.10¹⁵ s^-1 with the characteristic IR frequency of molecular hydrogen 0,1314.10¹⁵ s^-1. This increment of kinetic energy, as discussed in the previous example, is not available to an external observer, is not detected by the pressure or volume. And at the same time, the law of conservation of energy is conserved, since the kinetic energy within the molecule increased. Therefore, the kinetic energy of the orbital motion is thermodynamic entropy

4. Entropy of the gas

It was previously shown [ 5] that the substance in all three states have orbital motion of their constituent atoms and molecules. Condensed state is characterized by the orbital motion of a closed orbit - circular and elliptical, for gases at open orbits - parabolic and hyperbolic. The kinetic energy of parabolic and hyperbolic orbits has two components: the energy of translational rectilinear motion, initially communicated and kinetic energy due to the force of microgravity. We believe that the proposed definition of entropy as the orbital component of the kinetic energy of a moving particle is also true for the motion in an elliptical, parabolic and hyperbolic orbit. Orbital component of the kinetic energy can be characterized by the degree of deviation from the straight path of orbit.

Figure 2 schematically shows the elliptical (1), parabolic (2) and hyperbolic (3) orbits of the particle motion in a force center O (6) depending on the initial particle velocity v0. At speeds below the parabolic motion occurs in an elliptical orbit (1). If v0 = 2gm / r, the particle has a parabolic orbit (2) and goes into the gas phase. With further increase in the initial velocity movement occurs along a hyperbolic orbit (3), which is more close to the straight path.

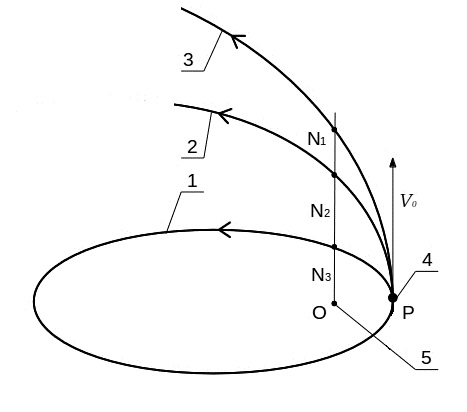
Fig.2. Scheme of particle P motion in an elliptical (1), parabolic (2) and hyperbolic (3) orbit. Orbital particle P with an initial velocity v0 (4), power center gm (5).

Deviation from the straight path, which characterizes the orbital component of the velocity and kinetic energy, respectively, are usually expressed orbital eccentricity. Figure 2 can be represented by the eccentricity of the orbit attitude segments:

    hyperbolic - (N₁O-OP) / OP> 1,
           parabolic - (N₂O-OP) / OP = 1,
           elliptic - (N₃O-OP) / OP <1.

The greater the eccentricity, the smaller the influence of the force center and correspondingly smaller orbital component of the kinetic energy and less entropy. In a straight line trajectory entropy component is completely absent.

The "disappearance" of the entropy component of the kinetic energy at low eccentricity explained blow molecule on the wall at an angle. This accordingly leads to underestimated values of the pressure and works pV compared with theoretical prescribed molecular-kinetic theory.

Conclusions

1. When the electron in a hydrogen atom from orbit r> 110 pm in orbit r = 4,167 pm potential energy decreases from 0 to -13.58 eV and half of the potential energy of 6.79 eV is realized in the form of electromagnetic radiation, and the second half in an amount of 6.79 eV is to increase the orbital kinetic energy of the electron. The latter does not depend on the external observer, "disappear" for him, though in reality it is present in the system, and the law of conservation of energy is conserved. Based on this we can assume that the kinetic energy of the orbital motion is the thermodynamic entropy.
2. When the formation of hydrogen atoms into hydrogen molecules closer ranging from 157 pm to 72 leads to the realization of the potential energy in a volume of 935 kJ / mol. Of this amount, 50%, or 467.5 kJ / mol is released in the form of electromagnetic radiation that is practically coincides with the value of the thermal effect of the formation of molecular hydrogen the reaction equal to 436 kJ / mol. The second half of the potential energy of 467.5 kJ / mol is to increase the orbital kinetic energy of the protons in a circular orbit around a common center of mass. This is confirmed by the coincidence of the calculated frequency of revolution 0,1295.10¹⁵ s^-1 with the characteristic IR frequency of molecular hydrogen 0,1314.10¹⁵ s^-1.
3. In the gas aggregate state, when the motion of the particles is carried out by open-parabolic and hyperbolic orbits, the entropy is an orbital component of the kinetic energy of the particles. This component is proposed to characterize by the deviation from the rectilinear motion of a particle trajectory by eccentricity of the orbit.

In conclusion, it would be desirable note the great insight R. Clausius, predicted need of introduction of function (entropy) into the law of energy conservation, which takes into account the disappearance of a fictitious energy of atoms and molecules. Verification of this function has been made possible only after breakthrough the atomic and molecular structure of the substance, and microgravity interactions of atoms and molecules, including their orbital movement relative to each other.

References

1. P. Atkins, Physical Chemistry,! 980, M. Ed. "Mir", Vol.1, p.146
2. A.T. Serkov, A.A. Serkov, Microgravity, electricity, forces of attraction and repulsion in the atom, http://www.sciteclibrary.ru/rus/catalog/pages/12915.html
3. A. T. Serkov, A. A. Serkov, The wavelength dependence of the characteristic X-ray chemical elements on their atomic radii and masses (third Kepler law in atomic systems)
   http://www.sciteclibrary.ru/rus/catalog/pages/11885.html
   http://www.sciteclibrary.ru/eng/catalog/pages/11886.html

4. AT Serkov, AA Serkov, Energy of chemical and intermolecular bonds, http://sciteclibrary.ru/rus/catalog/pages/12235.html
5. AT Serkov, VN Pokrovsky AA Serkov, About the upcoming change of the scientific paradigm in physics, http://www.sciteclibrary.ru/rus/catalog/pages/10375.html