© В.Н. Самохвалов
доктор технических наук, профессор
Контакт с автором: samohvalov_vn@mail.ru
Аннотация
На основе анализа результатов опытов физиков 18-19 веков по измерению величины отклонение тел при падении, опытов с маятником Фуко, определена причина расхождения результатов опытов и теории. Рассмотрена физическая сущность и особенности этих процессов, определяемые действием массодинамических полей.
____________________________________________________________________
Общепризнанные мнения и то, что считают делом давно решенным,
чаще всего
заслуживают исследования.
Георг Кристоф Лихтенберг (1742-1799)
Многие работы физиков 18-19 веков были посвящены исследованию траектории свободно падающих тел, исследованию поведения маятника Фуко, как экспериментального доказательства вращения земли. По истечению столетий ряд вопросов остались открытыми, т.к. некоторые, многократно наблюдавшиеся результаты этих опытов не находили теоретического объяснения [1].
Причина этого в том, что на движущиеся тела действуют ранее неизвестные массодинамические силы, которые влияют на эти процессы. Физическая сущность возникновения массодинамических полей и сил, а также ряд обусловленных ими физических процессов рассмотрены в [2-7]. Проведенный в этих работах анализ показывает, что действием массодинамических сил определяются многие процессы в природе.
1. Южное отклонение тел при падении
Предсказание Ньютона о восточном отклонении падающих тел от отвесной линии первым проверил Гульемини в 1791г. Однако наблюдая падение шаров с башни, наряду с восточным, он констатировал еще и южное отклонение, правда, незначительное. Лапласу такое отклонение показалось теоретически невозможным, и он сделал вывод, что все эти опыты неточны. Но Бенценберг повторил эти опыты, с возможно большими предосторожностями внутри колокольни в 1802г. Однако в его опытах снова выявилось южное отклонение 3,409 мм, что значительно больше возможного предела ошибок. К подобным же результатам привели опыты, которые провел Бенценберг в 1804 году в каменноугольной шахте. На основании своих исследований он пришел к заключению, что южное отклонение могло произойти только от естественной причины, не принятой в расчёт в теоретических выкладках [1].
В 1831 году Рейх снова занялся опытами с падающим телами с тем, чтобы вновь детально исследовать вызываемые вращением земли отклонения падающих тел от отвесной линии. В результате многочисленных опытов в шахте во Фрейберге он также нашел, что при высоте падения в 158,54 м, кроме восточного, выявилось и необъяснимое южное отклонение в 4,374 мм. По расчетам Гаусса и Ольберса величина южного отклонения, без учета сопротивления воздуха, не должна была превышать 0,01 мм. Поэтому найденное Рейхом южное отклонение осталось по существу дела неразъясненным, хотя оно и не было сведено к ошибкам наблюдения [1]. Результаты вышеописанных опытов представлены в таблице 1.
Причины отклонения расчетных и экспериментальных данных величины восточного отклонения тел при падении рассмотрены в работах автора [2] и [5] и объясняются действием масодинамических сил на движущуюся массу. Южное отклонение тел при падении обусловлено также действием массодинамических сил.
Таблица 1 – Опыты по измерению отклонения падающего тела от вертикали
| Наблюдатель |
Место опытов |
Число опытов |
Высота, h, м |
Наблюдавшееся восточное отклонение, D В, мм |
Наблюдавшееся южное отклонение D Ю, мм |
| Гуглиемини, 1791г. | Болонья | 16 | 78,3 |
19 |
+ |
| Бенценберг, 1802г. | Гамбург | 31 | 76,34 |
9,0 |
3,409 |
| Бенценберг, 1804г. | Шлеебуш | 29 | 85,1 |
11,5 |
+ |
| Рейх, 1831г. | Фрейбург | 106 | 158,5407 |
28,396 |
4,374 |
Основным фактором, приводящим к южному отклонению тел при падении является массодинамическая сила FМ - сила воздействия массодинамического поля Земли - МДП(З) на движущуюся в нем массу [2, 3]:
FМ = m× НВ´ VQ ,
где НВ – вертикальная составляющая массодинамического поля вращения Земли вокруг оси, VQ – окружная скорость движения тела относительно центра Земли в начальной точке, m – масса тела.
По своей физической сущности эта сила аналогична силе Лоренца при движении электрического заряда во внешнем магнитном поле. Вектор массодинамической силы FМ направлен по меридиану в югу. Эта сила и приводит к появлению южного отклонения при свободном падении тел.
Кроме того, наблюдавшееся в вышеприведенных опытах изменение величины наблюдавшегося южного отклонения тел при падении обусловлено наличием переменной широтной составляющей напряженности суммарного массодинамического поля вблизи поверхности земли [2, 3]. Она создает направленную по меридиану, переменную во времени массодинамическую силу FП:
FП = m× НШ(S ) ´ VП,
где НШ(S ) – широтная составляющая суммарного массодинамического поля, VП – скорость падения тела.
Широтная составляющая суммарного массодинамического поля обусловлена, в первую очередь, наложением на массодинамическое поле вращения Земли вокруг своей оси массодинамического поля вращения Земли вокруг Солнца – МДП(З-С).
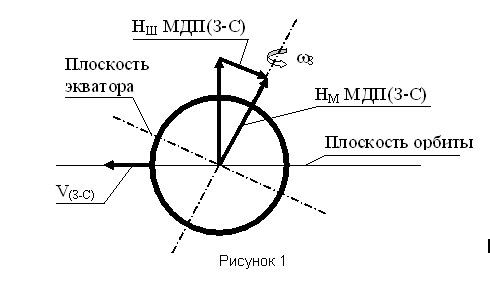
Ось вращения Земли вокруг оси имеет наклон к плоскости орбиты, поэтому силовые линии МДП(З-С) имеют широтную составляющую, зависящую от времени суток и времени года. Величина широтной составляющей напряженности этого массодинамического поля НШ(З-С) максимальна весной и осенью в дневное время, а минимальна летом и зимой в это же время суток (рисунок 1).

Вектор напряженности широтной составляющей от МДП(З-С) – НШ(З-С), весной (днем) направлен с востока на запад и определяемая им массодинамическая сила уменьшает южное отклонение тел при падении. Осенью наоборот – вектор широтной составляющая от МДП(З-С) (днем) направлен с запада на восток, т.е. южное отклонение увеличивает.
В меньшей степени широтную составляющую также дает массодинамическое поле вращения Луны вокруг Земли - МДП(Л-З) – месячный цикл, т.к. есть наклон плоскости орбиты Луны к оси Земли, а также массодинамическое поле вращения Солнца вокруг оси - МДП(С) – годовой цикл [2, 3].
Поскольку величина широтной составляющей напряженности суммарного массодинамического поля околоземного пространства НШ(S ) переменна в течении времени года, времени суток и фаз Луны, то величина южного отклонения падающих тел в проводившихся опытах, определяемая действием массодинамических сил, изменялась в достаточно больших пределах, что и обусловило наблюдавшийся достаточно большой разброс величины южного отклонения тел при падении.
Вектор меридиональной составляющей напряженности МДП(З-С) также меняется в течении времени суток. Днем вектор напряженности НМ(З-С) всегда направлен с юга на север, т.е. совпадает по направлению с вектором напряженность МДП(З), но его величина изменяется в течении времени года. Ночью вектор меридиональной составляющей напряженности МДП(З-С) направлен с севера на юг, утром и вечером его величина переходит через ноль, что приводит к значительному изменению массодинамических сил действующих на свободно падающее тело. Это определяло, при прочих стабильных условиях опытов, наблюдавшийся разброс величины восточного отклонения тел при падении (помимо погрешностей опытов).
Таким образом, действие изменяющихся во времени массодинамических сил объясняет появление южного отклонения при падении тел и разброс величины отклонения тел от вертикали при падении в опытах, представленных в работе [1].
2. Отклонения от закона вращения маятника Фуко
Другим доказательством вращения Земли в 18-19 веках были опыты Фуко. Свои первые опыты Фуко произвел в подвальном помещении с маятником длиной 2 м. По прошествии получаса маятник показывал уже заметное отклонение от первоначального направления своего колебания. Тот же результат, но более заметный, получился при повторении этих опытов в меридианном зале Парижской обсерватории с маятником в 11 м длины. Фуко опубликовал результаты этих исследований и высказал следующий закон: “Видимое вращение плоскости колебания маятника равно произведению углового движения земли на синус географической широты места подвеса маятника”.
Маркс, Кумб, Мариньяк, Юнг, Сильвестр, Таккер, Анстис, Клаузен, Шаар, Габбрайт и Гаутон, Эри, Крэгей, Беллавитис, Вудбург, Эшвейлер и другие уже в 1850 и 1851 гг. дали многочисленные доказательства этого закона, но при этом неоднократно обнаруживались и отклонения от закона вращения Фуко [1].
Т.Бунт путем точных измерений при помощи маятника длиной в 53 фут., подвешенного в церкви св. Николая в Бристоле, нашел, что часовое отклонение маятника составляло от 11°,677 до 11°,814, тогда как теоретически исчисленное отклонение было равно 11°,763. Дюфур, Вартман и Мариньяк нашли, что маятник отклонялся от местного меридиана как начальной плоскости своего колебания медленнее чем от перпендикулярной к меридиану плоскости. Разница была слишком велика, чтобы ее можно было объяснить ошибками наблюдения. Было предположено, что существует какая-то зависящая от общего движения возмущающая причина, которая отклоняет маятник от плоскости, перпендикулярной к меридиану, больше, чем от плоскости этого последнего [1].
Эта возмущающая причина проявляется таким образом, что колебания маятника, начинающиеся в плоскости, перпендикулярной к меридиану, становятся эллиптическими, тогда как обычно они оставались точно в одной плоскости. Дюфур полагал, что этой возмущающей силой может быть центробежная сила вращающейся земли. Эти интересные наблюдения нашли много сторонников, но встретили также немало возражений. Зантедески подтвердил их без всяких оговорок, но Уокер пришел к совершенно противоположным результатам, а Моссоти нашел, что влияние азимута на скорость вращения вообще незаметно. Наблюдавшийся флорентийскими академиками регулярный переход плоских колебаний маятника в эллиптические вызвал удивление наблюдателей, но открыть причин этого явления им не удалось [1].
В результате исследователи пришли к заключению, что вернее всего будет искать объяснение всех неправильностей в ходе колебаний маятника и вращения плоскости качаний не во вращении земли, а в случайных, но, тем не менее, почти всегда действующих причинах, как влияние способа подвеса и пуска маятника, сопротивление воздуха, воздушные потоки и т.п.
У маятниковых часов также наблюдаются циклические вариации ходов, имеющие суточный, лунно-месячный и годичный периоды. Эти эффекты не объясняются в рамках подхода общей теории относительности, поскольку для наземных часов весьма слабо изменяются расстояния до Луны и Солнца, т.е. недостаточно сильно изменяется гравитационный потенциал [8].
Как показано в работах автора [2] и [6], на основе большого числа экспериментальных исследований процесса колебаний короткого маятника с большой относительной амплитудой, причина отклонения движения маятника от закона Фуко прежде всего обусловлена действием на него сил со стороны изменяющегося во времени массодинамического поля. Причем отклонения от закона имеют не только количественный, но и качественный характер – смена направления вращения плоскости маятника и т.п. Действием изменяющихся массодинамических полей (описанных в 1-м разделе) обусловлены вышеуказанные циклические вариации ходов маятниковых часов, так же неоднократно фиксировавшиеся и автором.
Так как маятник жестко связан с землей через нить подвески, то при произвольном начальном положении плоскости качания маятника на него действуют в направлении перпендикулярном плоскости качания кориолисова сила FK:
FK=2mw VГ× sinj ,
где VГ – горизонтальная составляющая скорости движения маятника, j - широта.
На каждом цикле колебаний эта сила вызывает отклонение траектории движения маятника вправо (для северного полушария Земли) от направления горизонтального перемещения маятника и приводит к повороту плоскости качания маятника по часовой стрелке (ПО) - (рисунок 2).
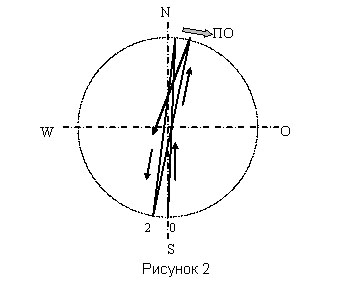
При этом маятнику одновременно, вследствие отклонения траектории от точки отвеса, придается некоторая поперечная скорость, которая приводит к появлению в общем законе движения маятника дополнительных поперечных колебаний. В результате, за счет действия поперечной силы и реакции нити возникает эллиптическое движение маятника и вращение большой полуоси эллипса колебаний маятника против часовой стрелки (Пр) - (рисунок 3).
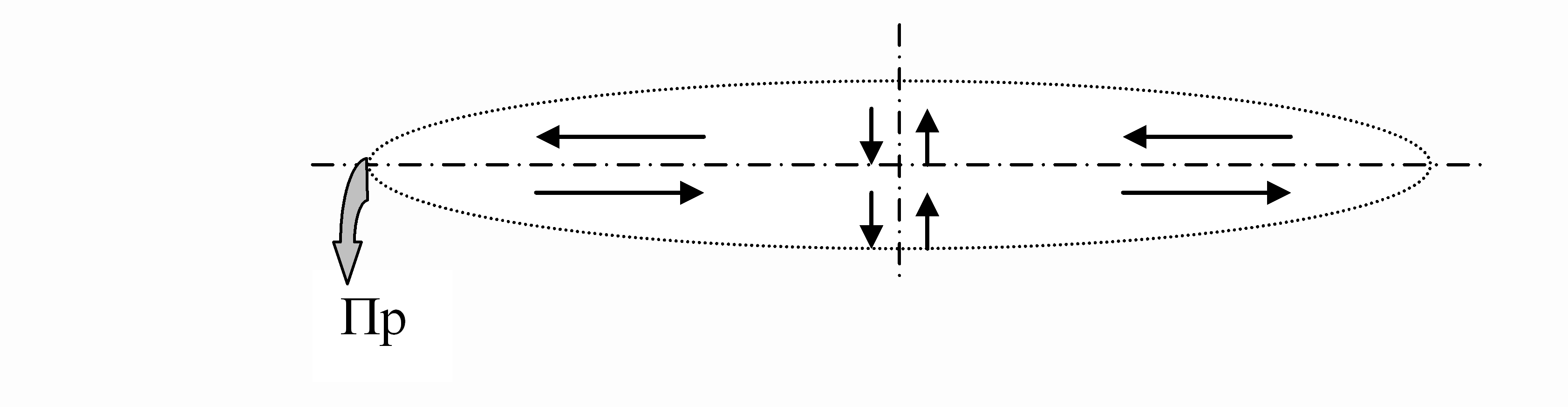
Рисунок 3
Однако эксперименты показали, что при большой начальной относительной амплитуде маятника, в диапазоне больших текущих амплитуд колебаний маятника существуют два сектора “I ” и “I I ” (рисунок 4), в которых поведение маятника, в процессе его колебаний, качественно отличается от вышеописанного.
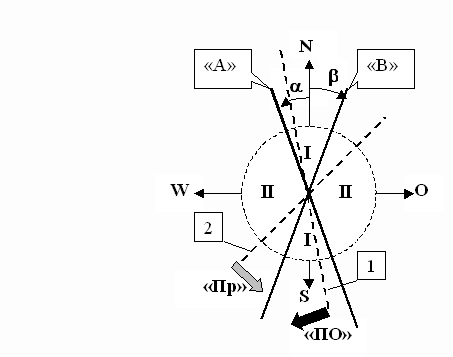
Рисунок 4
Если задавалась начальная плоскость колебаний маятника в секторе “I ”, т.е. между линиями “А” и “В” (поз 1, рисунок 4), то в процессе его колебаний, возникал поворот плоскости качания маятника по часовой стрелке − “ПО”, а также, в ряде случаев, заметный эллипс движения маятника в горизонтальной плоскости с вращением в туже сторону.
Если же начальная плоскость колебаний маятника задавалась в секторе “I I ” (поз.2, рисунок 4), то наблюдался поворот плоскости качания маятника против часовой стрелки “Пр” и значительный эллипс движения маятника также против часовой стрелки.
Если же начальная плоскость колебаний маятника задавалась на границе секторов “I ” и “I I ” (по линии “А” или “В”), то имела место относительно длительная устойчивость заданного начального положения плоскости качания маятника (отсутствие эллипса движения маятника в процессе его колебаний и отсутствие поворота плоскости качания).
В проведенных опытах с коротким маятником была значительная как горизонтальная, так и вертикальная составляющая скорости его движения. В этом случае на маятник действовали значительные массодинамические силы [2, 6].
Со стороны массодинамического поля вращения Земли вокруг оси - МДП(З), на маятник действуют следующие силы [2, 3]:
F1(З) =m[VГ´ НВ(З)], F2(З) =m[VГ´ НМ(З)], F3(З) =m[VВ´ НМ(З)],
где НВ и НМ, соответственно вертикальная и горизонтальная (меридиональная) составляющие напряженности массодинамического поля МДП(З), VГ и VВ – соответственно горизонтальная и вертикальная составляющие скорости движения маятника.
Сила F1(З) действует горизонтально и всегда нормальна мгновенной плоскости качания маятника, но ее действие по направлению противоположно кориолисовой силе FК [2, 6]. Эта сила вызывает отклонение траектории движения маятника вправо от точки его статического равновесия (в северном полушарии) и поворот плоскости качания против часовой стрелки и одновременно возбуждает эллиптическое вращение маятника по часовой стрелке, т.е. противоположно кориолисовой силе.
Сила F2(З) действует по вертикали и максимальна при колебаниях маятника в широтном направлении:
F2(З)=mVГ× НМ(З)siny ,
где y - азимут (угол между меридианом и плоскостью качания маятника).
При движении маятника с запада на восток F2(З) направлена вверх, а при движении с востока на запад − вниз. Она начинает влиять на процесс колебаний при наличии эллиптического движения маятника, когда есть угол между вертикалью и нитью подвески маятника. Таким образом, массодинамическая сила F2(З) вызывает несимметричность траектории движения маятника относительно точки его подвески, возбуждая эллиптическое вращение против часовой стрелки.
Сила F3(З) максимальна при колебаниях маятника в меридиональной плоскости, действует горизонтально и всегда нормальна мгновенной плоскости качания маятника:
F3(З)=mVВ× НМ(З)cosy
С учетом несимметричности траектории маятника от действия силы F2(З), эта сила приводит к возбуждению эллиптического вращения маятника по часовой стрелке.
Наложение вышеуказанных процессов определяет, в частности, результирующее направление поворота плоскости качания маятника.
При малых начальных значениях угла y действие F1(З) и F3(З) значительно нейтрализует возбуждение эллипса вращения маятника против часовой стрелки от действия кориолисовой силы FК. В результате происходит поворот плоскости качания маятника по часовой стрелке, но эллиптическое вращение маятника незначительно.
С увеличением начального значения угла y , массодинамическая сила F3(З) уменьшается, а сила F2(З) растет. В результате увеличивается вращение против часовой стрелки эллипса движения маятника, что приводит к повороту против часовой стрелки плоскости его колебаний.
Поскольку параметры вращения Земли вокруг своей оси неизменны, а, следовательно, массодинамическое поле Земли − МДП(З) постоянное, то при y =const также F1(З)=const и FК=const. Однако, суммарное массодинамическое поле, в пространстве, где расположен маятник, включает так же массодинамические поля вращения Луны вокруг Земли - МДП(Л-З), Земли вокруг Солнца - МДП(З-С) и собственного вращения Солнца вокруг оси - МДП(С) [2, 3]. Эти поля на поверхности земли переменны в течение времени, вследствие изменения взаимного положения Земли, Солнца и Луны, а, следовательно, изменяется величина и направление силовых линий этих массодинамических полей относительно плоскости качания маятника (при y =const).
Вследствие суточного вращения Земли, наклона оси Земли к плоскости ее солнечной орбиты и плоскости лунной орбиты происходит непрерывное изменение параметров суммарного массодинамического поля - МДП(S ). При этом изменяется как величина меридиональной и вертикальной составляющей напряженности суммарного массодинамического поля, так и возникает ее широтная составляющая.
Следствием этого является изменение во времени массодинамических сил, при неизменности FК (для фиксированного значения y и параметров маятника), а также появления дополнительных, переменных во времени, массодинамических сил от широтной составляющей НШ напряженности суммарного массодинамического поля:
F1(S )=m[VГ´ НВ(S )], F2(S )=m[VГ´ НМ(S )], F3(S )=m[VВ´ НМ(S )]
F4(S )=m[VГ´ НШ(S )], F5(S )=m[VВ´ НШ(S )],
где НВ(S ), НМ(S ) и НШ(S ), соответственно, вертикальная, меридиональная и широтная составляющая суммарного массодинамического поля.
Характер воздействия на маятник массодинамических сил F1(S ), F2(S ) и F3(S ) аналогичен, соответственно, описанному выше действию сил F1(З), F2(З) и F3(З), но эти силы переменны во времени по величине и направлению, т.к. переменна величина и направление вектора меридиональной составляющей напряженности суммарного массодинамического поля, что показано в 1-м разделе.
Воздействия на маятник массодинамических сил F4(S ) и F5(S ), определяемых переменной во времени широтной составляющей напряженности суммарного массодинамического поля (см. раздел 1), аналогично по характеру действия, соответственно, действию массодинамических сил F2(S ) и F3(S ). Эти силы также изменяют во времени свою величину и направление при неизменных начальных параметрах колебаний маятника.
Таким образом, действие изменяющихся во времени массодинамических сил определяет особенности процесса вращения плоскости колебаний маятника, его качественные и количественные отличия от закона Фуко, что зафиксировано в опытах представленных в работе [1] и в проведенных опытах автора [2, 6].
Литература
1. Электромагнитная волна (в религиозной терминологии релятивизма - "свет") имеет строго постоянную скорость 300 тыс.км/с, абсурдно не отсчитываемую ни от чего. Реально ЭМ-волны имеют разную скорость в веществе (например, ~200 тыс км/с в стекле и ~3 млн. км/с в поверхностных слоях металлов, разную скорость в эфире (см. статью "Температура эфира и красные смещения"), разную скорость для разных частот (см. статью "О скорости ЭМ-волн")
2. В релятивизме "свет" есть мифическое явление само по себе, а не физическая волна, являющаяся волнением определенной физической среды. Релятивистский "свет" - это волнение ничего в ничем. У него нет среды-носителя колебаний.
3. В релятивизме возможны манипуляции со временем (замедление), поэтому там нарушаются основополагающие для любой науки принцип причинности и принцип строгой логичности. В релятивизме при скорости света время останавливается (поэтому в нем абсурдно говорить о частоте фотона). В релятивизме возможны такие насилия над разумом, как утверждение о взаимном превышении возраста близнецов, движущихся с субсветовой скоростью, и прочие издевательства над логикой, присущие любой религии.
4. В гравитационном релятивизме (ОТО) вопреки наблюдаемым фактам утверждается об угловом отклонении ЭМ-волн в пустом пространстве под действием гравитации. Однако астрономам известно, что свет от затменных двойных звезд не подвержен такому отклонению, а те "подтверждающие теорию Эйнштейна факты", которые якобы наблюдались А. Эддингтоном в 1919 году в отношении Солнца, являются фальсификацией. Подробнее читайте в FAQ по эфирной физике.
|
|