В стоячей волне в отличие от бегущей средние по времени значения кинетической
и потенциальной энергий не равны друг другу в каждой точке:
При наличии в среде нескольких гармонических волн разных частот плотности
энергии складываются; для волн же одинаковой частоты плотности энергии не
аддитивны; например, при сложении двух одинаковых волн, когда амплитуды во всех
точках среды удваиваются, плотность энергии учетверяется.
Знаете ли Вы, что такое мысленный эксперимент, gedanken experiment?
Это несуществующая практика, потусторонний опыт, воображение того, чего нет на самом деле. Мысленные эксперименты подобны снам наяву. Они рождают чудовищ. В отличие от физического эксперимента, который является опытной проверкой гипотез, "мысленный эксперимент" фокуснически подменяет экспериментальную проверку желаемыми, не проверенными на практике выводами, манипулируя логикообразными построениями, реально нарушающими саму логику путем использования недоказанных посылок в качестве доказанных, то есть путем подмены. Таким образом, основной задачей заявителей "мысленных экспериментов" является обман слушателя или читателя путем замены настоящего физического эксперимента его "куклой" - фиктивными рассуждениями под честное слово без самой физической проверки.
Заполнение физики воображаемыми, "мысленными экспериментами" привело к возникновению абсурдной сюрреалистической, спутанно-запутанной картины мира. Настоящий исследователь должен отличать такие "фантики" от настоящих ценностей.
Релятивисты и позитивисты утверждают, что "мысленный эксперимент" весьма полезный интрумент для проверки теорий (также возникающих в нашем уме) на непротиворечивость. В этом они обманывают людей, так как любая проверка может осуществляться только независимым от объекта проверки источником. Сам заявитель гипотезы не может быть проверкой своего же заявления, так как причина самого этого заявления есть отсутствие видимых для заявителя противоречий в заявлении.
Это мы видим на примере СТО и ОТО, превратившихся в своеобразный вид религии, управляющей наукой и общественным мнением. Никакое количество фактов, противоречащих им, не может преодолеть формулу Эйнштейна: "Если факт не соответствует теории - измените факт" (В другом варианте " - Факт не соответствует теории? - Тем хуже для факта").
Максимально, на что может претендовать "мысленный эксперимент" - это только на внутреннюю непротиворечивость гипотезы в рамках собственной, часто отнюдь не истинной логики заявителя. Соответсвие практике это не проверяет. Настоящая проверка может состояться только в действительном физическом эксперименте.
Эксперимент на то и эксперимент, что он есть не изощрение мысли, а проверка мысли. Непротиворечивая внутри себя мысль не может сама себя проверить. Это доказано Куртом Гёделем.
Понятие "мысленный эксперимент" придумано специально спекулянтами - релятивистами для шулерской подмены реальной проверки мысли на практике (эксперимента) своим "честным словом". Подробнее читайте в FAQ по эфирной физике.
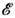 и равна
и равна
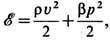
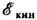 ,
а второй - плотность потенциальной энергии
,
а второй - плотность потенциальной энергии 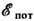 ; ρ - плотность среды; β = 1/ρс2 - сжимаемость
среды, с - скорость звука; u - колебательная скорость частиц; р - звуковое
давление.
; ρ - плотность среды; β = 1/ρс2 - сжимаемость
среды, с - скорость звука; u - колебательная скорость частиц; р - звуковое
давление.
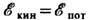 и плотность полной энергии
и плотность полной энергии
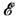 = ρu2
= βр2. В произвольной
= ρu2
= βр2. В произвольной 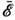 =
(λ/2)ρu20 = (λ/2)bp20, где u0
и p0 - амплитуды колебательной скорости и давления.
=
(λ/2)ρu20 = (λ/2)bp20, где u0
и p0 - амплитуды колебательной скорости и давления.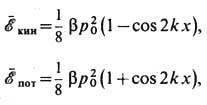
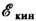 достигает максимума в узлах, а
достигает максимума в узлах, а  - в
пучностях давления. Средняя по времени (или по пространству) плотность полной
звуковой энергии в
- в
пучностях давления. Средняя по времени (или по пространству) плотность полной
звуковой энергии в 
