Эллипсометрия - метод неразрушающего измерения и контроля оптич. параметров
веществ по поляризац.
характеристикам отражённого (реже - проходящего) света. Поскольку наиб. общим
случаем (полной) поляризации является эллиптическая, метод и называется Э.
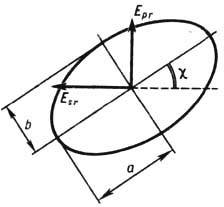
Рис. 1. Эллипс поляризации отражённой волны.
Эллипсометрия отражения. Если на плоскую поверхность однородной изотропной (в общем случае поглощающей)
среды падает линейно поляризованная плоская волна, имеющая электрич. вектор
E (составляющая Ер лежит в плоскости падения,
а перпендикулярная ей - Es ), то при зеркальном отражении
возникает плоская волна Er с компонентами
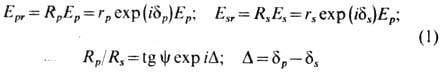
(см. Отражение света). В результате вектор Er будет описывать эллипс,
определяемый углами g и c (рис. 1):
где g-эллиптичность; c - азимут эллипса; а, b - его полуоси. Эти параметры легко связать с параметрами (1) соотношениями
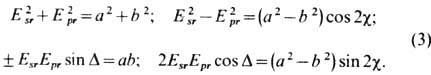
Значения Rp и Rs определяются углом падения f и оптич. свойствами
(коэф. преломления n и показателем поглощения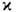 
[1-4], см. также Френеля формулы, Металлоопти-ка). T. о., зная f
и измеряя g и c (или y и D). можно определить указанные
оптич. свойства. [Знак " + " в (2) и (3) соответствует левому вращению,
если смотреть навстречу лучу, знак " -" - правому.]
Анализ формул Френеля показывает,
что фазовые характеристики отражённой световой волны чувствительнее к изменениям
оптич. параметров, чем амплитудные, к тому же измерения фазовых характеристик
могут быть проведены с большей точностью, чем амплитудных. Это обусловливает
широкое применение Э. отражения. Для анизотропных сред необходимы измерения
в неск. плоскостях падения. Для поглощающих кристаллов любых симметрии наиб.
общий метод заключается в измерении на одном аншлифе параметров эллипсов при
одном угле падения для трёх плоскостей падения и при другом для одной плоскости
[5]. Более простые методы пригодны лишь для высоких симметрии без поглощения.
Если объект представляет
собой плоский слой, толщина к-рого d сравнима с глубиной проникновения
света, учитывают многократные отражения внутри слоя. Применяются расчёты по
методам парциальных волн [2], образующих выходящую волну, или решения волнового
ур-ния в данных граничных условиях [1 ]. Макроскопич. расчёт пригоден при d>>a,
где а - характерный микроскопич. размер среды, напр. постоянная решётки,
длина пробега электрона и т. п. Для слоя с переменными по толщине параметрами
макроскопич. расчёт был дан П. Друде (P. I. Drude, 1898), но лишь для d<<l. Знание двух параметров эллипса позволяет определить два параметра среды.
В формулы, связывающие эллиптичность с оптич. параметрами слоя, входит его толщина;
разработаны методики измерений и расчётов, позволяющие определить все три параметра.
Так, напр., проводят измерения при двух определ. образом выбранных углах падения
или при двух разл. иммерсиях и т. п.
Особенно подробно разработана
Э. тонких слоев на массивной подложке. Здесь g и c зависят от 7 переменных
- n1, n2,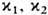 
, j, d, l.
Для многослойных сред теория
сложнее; в совр. Э. используется чаще всего Джонса матричный метод (рассеянием
в системе обычно пренебрегают). Решение прямой задачи (вычисление параметров
эллипса поляризации по параметрам среды) математически менее трудно, чем обратной
(определение параметров среды по параметрам эллипса), к-рая обычно требует численных
расчётов разл. методами [2, 4, 7]. Поэтому Э. получила особенное развитие после
применения ЭВМ, решающих матем. проблемы.
Физ. проблема совр. Э.
заключается в уточнении связи параметров поляризации со свойствами среды. Формулы
Френеля получены из граничных условий на геом. плоскости, разделяющей однородные
сплошные среды, и поэтому являются первым приближением. Микроскопич. расчёты
показывают, что отражённая волна формируется в неск. приповерхностных молекулярных
слоях и содержит информацию именно о них; связь с параметрами вещества в объёме
должна устанавливаться теоретически (см. Поверхность ).Так, при отражении
от поверхности металла необходимо иметь в виду, что здесь имеется два физически
выделенных поверхностных слоя: один обусловлен шириной потенциального барьера
и областью пробега отражённых от него электронов, а другой - текстурой, возникшей
при обработке поверхности. Второй может быть устранён спец. приёмами, напр.
ионной бомбардировкой, электрополировкой и др.; связь свойств первого со свойствами
в толще определяется уже теоретич. соображениями. Из формул Френеля следует,
что линейно поляризованный свет, отражаясь от поверхности прозрачной среды,
остаётся линейно поляризованным, однако сам факт дискретности структуры среды
влечёт за собой возникновение нек-рой, очень небольшой (b/а~ 10-5),
эллиптичности. Теоретически и экспериментально [3] было показано, что на поверхности
чистой жидкости под вакуумом, т. е. находящейся в равновесии со своим паром,
имеется моно- или бимолекулярный слой ориентированных молекул, что и создаёт
эллиптичность (b/а~10-3). Для открытой поверхности
на это указал ещё P. Рэлей (R. Rayleigh, 1882) и А. Буэ (A. Bouhet, 1931). Теории
возникновения эллиптичности для тонких слоев металлов см. в [6]; для моно-,
бимолекулярных и подобных им слоев также разработаны нек-рые теоретич. подходы
[2, 3, 7].
Преимуществом эллипсометрии отражения является возможность исследования именно поверхностных слоев, недостатком - трудности неизбежно косвенного определения свойств в объёме.
Эллипсометры. Существует
большое разнообразие их конструкций [2]. Источник света, как правило,- лазер,
приёмник - фотоэлектрический. Принципиальная схема нек-рых вариантов дана на
рис. 2. В одном из них падающий свет поляризован линейно (линейный поляризатор
П), в отражённом луче эллиптически поляризованный свет компенсатором оптическим К превращается (подбором ориентации и разности фаз компенсатора) в поляризованный
линейно, азимут колебаний к-рого определяется линейным анализатором А по погашению
сигнала в приёмнике. В др. варианте (пунктир) падающий свет поляризован эллиптически,
а параметры эллипса устанавливаются так, чтобы после отражения поляризация была
линейной и сигнал гасился А (нулевые схемы). В др. конструкциях в обоих вариантах
добиваются в отражении циркулярной поляризации, получение к-рой устанавливается
по неизменности сигнала при вращающемся анализаторе.
Рис. 2. Принципиальная
схема эллипсометра: Л - лазер; F
- фотоэлектрический приёмник света; П - поляризатор;
А - анализатор; К - компенсатор; M - модулятор света.
Обычно для повышения точности
измерений используется модуляция света (напр., небольшим качанием плоскости
поляризации) с помощью пьезооптич., электрооптич. или магнитооптич. модуляторов
света.
Иногда параметры эллипса
меняют изменением угла падения. Часто в приборах предусматривается сканирование
по длинам волн. В 90-х гг. разработаны нелинейные эллипсометры, в к-рых мощная
накачка создаёт в среде нелинейные эффекты, а слабый пробный луч используется
для эллипсометрич. измерений.
Методы отражат. Э. применяются
для исследования веществ с большим поглощением (металлы, полупроводники), ибо
исследования в таких слоях, к-рые ещё дают пропускание (для металлов- 10-50
нм), в силу структурных особенностей таких слоев не дают сведений о свойствах
в объёме. Особенно широко исследуются тонкие слои - эпитаксиальные слои, слои
окислов, адсорбционные и адгезионные, слои, создаваемые ионной имплантацией,
всякого рода металлич. и диэлектрич. покрытия и т. д. Разработаны методы исследования
кинетики роста слоев и плёнок; Э. даёт возможность контроля непосредственно
в течение процесса.
Э. пропускания основана на тех же принципах - измерении параметров эллипса прошедшего через вещество света (при полной поляризации). В Э. пропускания практически не выделяется влияние поверхностных слоев на фоне влияния основной толщи; она применяется для измерения оп-тич. параметров слабо поглощающих кристаллов, для измерения естеств. и магн. вращения плоскости поляризации, естеств. и магн. кругового дихроизма, поскольку для этих параметров теория отражения слабо разработана и трудна для вычислений, и измерения по отражению дают малую точность. Для таких измерений чаще используются поляриметры и рефрактометры .Приборы для Э. пропускания чаще наз. кристаллорефрактометрами, дихрографами и др. Существует термин "Э. рассеяния" - измерение частичной поляризации света при прохождении мутных сред, аэрозолей, коллоидов - однако он малоупотребителен.
В. А. Кизель.
|
|
 |
