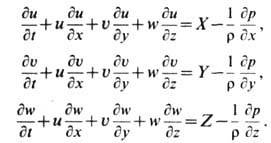
Эйлера уравнение в гидромеханике - дифференц. ур-ние движения идеальной жидкости в переменных Эйлера. Если давление р, плотность р, проекции скоростей частиц жидкости и, v, w к проекции
действующей объёмной силы X, Y, Z рассматривать как функции координат х,
у, z точек пространства и времени t (переменные Эйлера), то
Э. у. в проекциях на оси прямоуг. декартовой системы координат принимает вид
системы ур-ний:
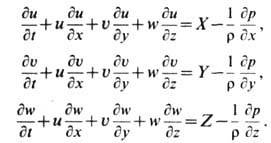
Решение общей задачи гидромеханики в переменных
Эйлера сводится к тому, чтобы, зная X, Y, Z, а также начальные и граничные
условия, определить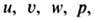
р как функции х, у, z и t. Для этого к Э. у. присоединяют ур-ние
неразрывности в переменных Эйлера:
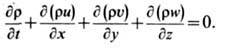
В случае баротропной жидкости, у к-рой плотность
зависит только от давления, 5-м ур-нием будет ур-ние состояния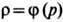 
(или
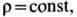когда
жидкость несжимаема).
Э. у. пользуются при решении разнообразных
задач гидромеханики.
|
|
 |
