Фурье-оптика - раздел оптики, в к-ром преобразование световых полей оптич. системами исследуется с
помощью фурье-анализа (спектрального разложения) и теории линейной фильтрации.
Начало использования в оптике идей спектрального разложения связано с именами
Дж. Рэлея (J. Rayleigh) и Э. Аббе (Е. Abbe). Первые работы, к-рые легли в основу
совр. Ф--о., принадлежат Мандельштаму [1], Горелику [2], Рытову [3]. В последней
проводится аналогия между задачами радиоэлектроники и теории связи, с одной
стороны (в к-рых речь идёт о преобразовании сигналов-функций времени-изменяющихся
токов, напряжений и т. д. и о системах радиоэлектроники, регистрирующих эти
преобразования), и задачами оптики- с другой, в к-рых рассматривается преобразование
световых полей-функций координат-оптич. системами.
Общность методов исследования
систем, служащих для преобразования сигналов - функций времени (временных фильтров),
и оптич. систем, служащих для преобразования световых полей - функций координат
(пространств. фильтров), обусловлена общностью закономерностей, управляющих
процессами в системах радиоэлектроники и оптики, общностью, заложенной в универсальности
максвеллов-ских ур-ний электродинамики. И тем и другим системам присущи (в достаточно
широкой области применений) такие фундаментальные свойства, как линейность и
инвариантность. Это позволяет удобно и просто описывать их поведение единым
образом, используя универсальный аппарат теории линейной фильтрации и преобразования
Фурье.
Основные понятия и соотношения
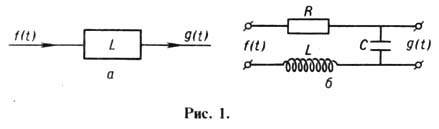
Ф--о. В радиоэлектронике систему, преобразующую сигналы, принято изображать
в виде схемы (рис. 1, а), где внеш. воздействие f(t) есть
входной сигнал фильтра, а результат этого воздействия g(t) - выходной
сигнал (или отклик) фильтра. Примером временного фильтра является колебат. контур
(рис. 1, б), в к-ром внеш. эдс - входной сигнал, а возникающие
изменения напряжения на обкладках конденсатора- отклик фильтра. Тот факт, что
функция g(t)является откликом на входное воздействие f(t),
записывают в виде операторного равенства
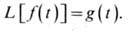
Волновые (в частности,
оптические) явления характеризуются как временной зависимостью, так и пространственной,
т. е. зависимостью от координат. В Ф--о. интерес представляет именно пространств.
структура волны, к-рая описывается (в случае гармонич. волн фиксированной частоты
w) комплексной амплитудой волны f(x, у, z), являющейся решением ур-ния
Гельмгольца:
(k = w/c- волновое
число). [Комплексная амплитуда, определяющая распределение амплитуд и фаз колебаний
является входным и выходным сигналом когерентной оптич. системы. При некогерентном
освещении говорят о картинах интенсивности (а не об амплитудах) во входной и
выходной плоскостях.]
В процессе распространения
волны через оптич. систему её пространств. структура изменяется. Такая система
рассматривается как пространственный фильтр, преобразующий входной сигнал (комплексную
амплитуду волны во входной плоскости оптич. системы) в выходной сигнал (комплексную
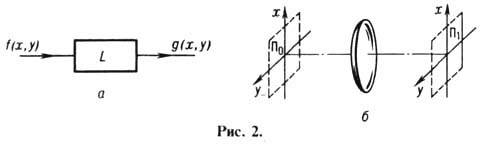
амплитуду волны в выходной плоскости оптич. системы). На рис. 2 представлена
схема пространств. фильтра (а)и пример простейшей оптич. системы (б), где f(x, у) - комплексная амплитуда волны во входной
плоскости П0, g(x, у) - комплексная амплитуда в выходной плоскости
П1. Соответствующее операторное равенство имеет вид
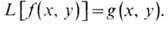
В радиоэлектронике свойства
линейного фильтра характеризуются импульсным откликом h(t, t)
- откликом фильтра на входной d-импульс:
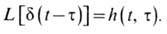
Здесь h(t, t) -
функция времени t, параметр t указывает, что речь идёт об отклике на d-импульс,
возникающий на входе в момент времени t = t.
Аналогом d-импульса, возбуждающего
колебания в линейном фильтре, в задачах пространств. фильтрации является точечный
источник света d(x -x, у - h), расположенный в точке x
= x, у = h входной плоскости ху. При этом в выходной плоскости
возникает нек-рое световое поле с комплексной амплитудой h(x, у; x, h), являющейся функцией координат х, у в выходной плоскости. Поле
h(x, у; x, h) наз. ф у н к ц и е й р а с с е я н и я т о ч к и
и является аналогом импульсного отклика линейного временного фильтра.
Временные фильтры подчиняются
принципу причинности: сигнал на выходе фильтра не может появиться раньше входного
сигнала, импульсный отклик h(t, t) отличен от нуля лишь при t>=t.
Различие в физ. смысле переменных (времени t и координат х, у)приводит
к важному различию временных и пространств. фильтров: принцип причинности в
задачах пространств. фильтрации не выполняется: точечный источник света, расположенный
в начале координат х = 0, у = 0 входной плоскости, приводит
к возникновению светового поля в выходной плоскости как при х,у>0, так и при х,у<0.
Если изменение момента
появления d-импульса на входе не меняет вид функции импульсного отклика, а лишь
сдвигает её во времени h(t, t) = h(t - t), то временной фильтр
наз. с т а ц и о н а р н ы м. Примером является колебат. контур с постоянными,
не зависящими от времени параметрами L, С, R.
Аналогичное свойство пространств.
фильтра наз. и з о-п л а н а т и ч н о с т ь ю: сдвиг точечного источника во
входной плоскости приводит лишь к сдвигу функции рассеяния в выходной плоскости:
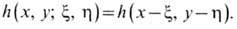
Как правило, изопланатичность
оптич. систем выполняется лишь при малых значениях параметров x, h. Стационарный
временной фильтр, а также изопланатичный пространств. фильтр наз. и н в а р
и а н т н ы м и ф и л ь т р а м и.
Если известен импульсный
отклик временного линейного фильтра, то задача фильтрации (нахождение отклика
по заданному входному сигналу) решается с помощью интеграла суперпозиции:
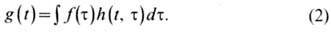
Аналогично решается задача
пространственной фильтрации- нахождение комплексной амплитуды волны в
выходной плоскости по заданному полю во входной плоскости:
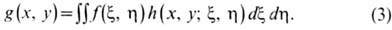
Если речь идёт об инвариантных
фильтрах, то вместо (2) и (3) имеем
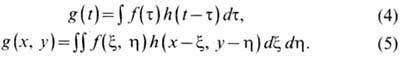
Интегральная операция в
(4) или (5)наз. свёрткой функций f(t) и h(t)в (4) или
д в у м е р н о й свёрткой функций f(x, у)и п(х, у)в (5). Символически
операции свёртки (4) и (5) записываются в виде
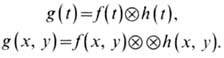
Инвариантность линейных
фильтров позволяет перейти к спектральному описанию. Используя известную теорему
фурье-анализа о фурье-образе свёртки, связь между спектрами (фурье-преобразованиями)
входного и выходного сигналов можно записать в виде
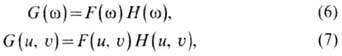
где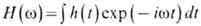 
-частотная характеристика временного фильтра, а Н(и, u) - частотная
характеристика пространств. фильтра, являющаяся фурье-преобразова-нием функции
рассеяния точки:
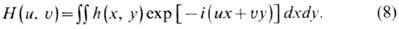
Одно из важнейших преимуществ
спектрального подхода- простота операции, связывающей спектры сигналов на входе
и выходе фильтра. Представление сигнала f(t) в виде интеграла
Фурье
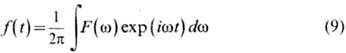
имеет ясный физ. смысл:
равенство (9) утверждает, что сигнал f(t)может быть представлен суммой
гармонич. колебаний, причём спектр F(w) = A(w)ехр ij(w)
определяет вклады гармоник разл. частот - их амплитуды A(w) и нач. фазы
j(w).
Гармонич. колебания ехр
iwt имеют особое значение в задачах линейной фильтрации: при возбуждении
ими линейного стационарного фильтра в последнем возникают вынужденные гармонич.
колебания той же частоты w. Др. словами, гармонич. функции ехр iwt
являются собств. функци-ями линейной стационарной системы. Это можно записать
в виде операторного равенства
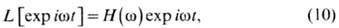
где H(w) = В(w)ехр
ia(w)-частотная характеристика фильтра, определяющая амплитуду В (w)
и сдвиг по фазе a(w) вынужденных колебаний относительно внеш. воздействия.
Пространственное фурье-разложение. Комплексную амплитуду волны f(х, у)можно представить в виде
интеграла Фурье [двумерный аналог ф-лы (9)]:
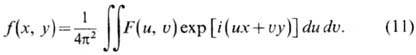
Физ. смысл разложения (11)
состоит в следующем. Можно проверить, что функция
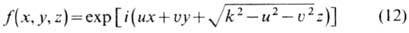
является решением ур-ния
Гельмгольца (1), удовлетворяющего на плоскости z = 0 граничному условию
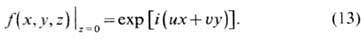
Это утверждение справедливо
при любых значениях параметров и, u. функция (12) есть комплексная
амплитуда плоской волны, причём параметры и, u - проекции волнового
вектора k этой волны на оси х, у, если |u2
+ u2|<= <=(w/c)2 = k2. Если же |u2 + u2|>k2, выражение (12) также является решением (1) и наз. н е о д н о р о д н о
й в о л н о й (амплитуда волны спадает с ростом z экспоненциально, поскольку
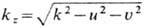-в этом
случае мнимое число).
Т. о., выражение (11) есть
представление произвольной волны, заданной в нек-рой плоскости z = const, в
виде суперпозиции плоских волн, как бегущих, так и неоднородных.
Плоская волна ехр[i(ux
+ uy)] в задачах пространств. фильтрации является аналогом гармонич.
колебания ехр iwt. Поэтому пару чисел и, u наз.
пространственными частотами.
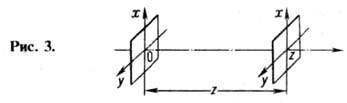
Частотная характеристика
свободного пространства. Участок свободного пространства между двумя плоскостями
z = 0 и z = const > 0 (рис. 3) является простейшим пространств. фильтром.
Согласно (12) и (13), распространение плоской волны между двумя плоскостями
приводит лишь к появлению множителя ехр [i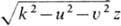
], определяющего
набег фазы волны (при |u2 + u2|<=k2)или экспо-ненц. уменьшение амплитуды (при |u2 + u2|>k2). Это утверждение можно записать в виде операторного равенства:
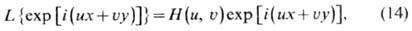
где Н(и, u) = ехр(i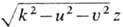
) - частотная характеристика свободного пространства. Экспоненц. функции ехр[i(ux+uy)]
при любых (и, u)являются, согласно (14), собственными функциями
пространств. фильтра.
Пространственная модуляция. В радиоэлектронике модуляция сигнала записывается как операция перемножения
модулируемого колебания f(t) и модулирующего сигнала m(t), в результате к-рой на выходе модулятора имеем модулированный сигнал g(t)=f(t)m(t). Различают два вида модуляции: амплитудную, когда m(t) - действительная
положит. функция a(t), и фазовую: m(t) = ехр ij(t).
Если несущее (модулируемое) колебание - гармонич. функция f(t) =
= ехр iwt, то в первом случае на выходе имеем амплитуд-но-модулированное
колебание g(t) = a(t)exp iwt, а во
втором- колебание, модулированное по фазе g(t) = = ехр{i[wt+j(t)]}.
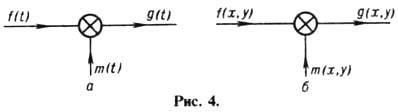
Операцию модуляции изображают символически с помощью блок-схемы (рис. 4, а).
Пространств. модуляция
осуществляется в оптике с помощью тонких пластинок-транспарантов,- обладающих
в разных точках разл. поглощательной способностью и (или) показателем преломления.
При освещении пластинки плоской волной expi(ux + uy)это приводит
к тому, что амплитуда волны на выходе из пластинки оказывается различной в разных
точках (в соответствии с изменением поглощат. способности), т. е. имеем амплитудную
модуляцию волны:
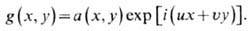
Если пластинка имеет различный
в разных точках показатель преломления п(х,у)[или толщину h(x,y)], то набег фазы волны при прохождении пластинки оказывается в разных местах
различным: j(х, y) = kn(x,y)h(x,у) - получается фазовая модуляция:
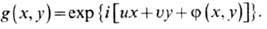
В общем случае с помощью
транспаранта осуществляется как амплитудная, так и фазовая пространств. модуляция.
функция m(x,y) = a(x,y)exp
ij(x,y), определяющая характер пространств. модуляции и связывающая
комплексную амплитуду волны на входе и выходе транспаранта g(x,y) = =
т (х, y)f(x, у), наз. функцией п р о п у с к а н и я (или модуляц. характеристикой)
транспаранта. Операция пространств. модуляции изображается с помощью блок-схемы,
изображённой на рис. 4(б). Для осуществления пространств. модуляции в
оптике используют различного вида маски, пластинки, амплитудные и фазовые решётки.
Преобразование Фурье,
осуществляемое линзой. Осн. элементом любого оптич. устройства является
линза. Идеальная безаберрационная линза осуществляет фазовую модуляцию вида
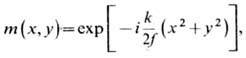
где f-фокусное расстояние
линзы. В оптике пространств. спектральное разложение тесно связано со свойством
линзы фокусировать параллельный пучок света: падающая на линзу плоская волна
expi(ux+uy)с пространств. частотой (и, u)фокусируется
линзой в точку фокальной плоскости с координатами x=fu/k и y=fu/k (рис. 5). Падающая на линзу произвольная волна с комплексной амплитудой
f(x,y)может быть представлена, согласно (11), суперпозицией плоских
волн разных направлений (т. е. разных пространств. частот и, u), и
каждая из плоских волн в этой суперпозиции фокусируется линзой в свою определ.
точку фокальной плоскости, создавая в ней световое поле с амплитудой, пропорциональной
амплитуде соответствующей волны, и с фазой, определяемой фазой соответствующей
волны, т. е. создавая в ней колебание, пропорциональное величине F(kx/f,
ky/f), где F(u, u) - преобразование Фурье функции f(х,
у). Т. о., световое поле, возникающее в фокальной плоскости линзы, представляет
собой пространств. спектральное разложение волны, падающей на линзу.
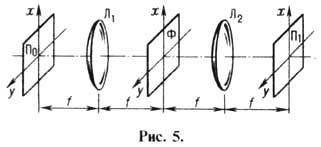
Теория Аббе формирования
изображения (принцип двойной дифракции). На рис. 5 в качестве примера оптич.
системы, формирующей изображение, приведена система, состоящая из двух линз
Л1 и Л2 с общей фокальной плоскостью Ф; входной плоскостью
П0 (где размещается предмет) служит передняя фокальная плоскость
линзы Л1, а выходной плоскостью, где возникает изображение,- задняя
фокальная плоскость линзы Л2 - плоскость Пt.
Формирование изображения
в оптич. системе, согласно теории Аббе,- двухэтапный процесс. Первый этап (первая
"дифракция")-это распространение света от входной плоскости до плоскости
Ф, где формируется пространств. спектр предметной волны. На этом этапе линза
Л1 осуществляет первое пространств. фурье-преобразова-ние.
Второй этап (вторая дифракция) - распространение света от плоскости Ф (к-рая
наз. фурье-плоскостью оптич. системы) до плоскости изображения. На этом этапе
линза Л2 осуществляет ещё одно преобразование Фурье. В результате
двух последоват. преобразований Фурье возникает перевёрнутое изображение-поле
с комплексной амплитудой g(x,y)=f(-x, -у), тождественное с точностью
до инверсии предметному полю f(х, у).
Частотная характеристика
оптической системы формирования изображения. Описанная выше оптич. система
является идеальной: изображение, тождественное предмету, создаётся системой
с частотной характеристикой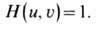 
В действительности же оптич.
система вносит искажения. Принципиальными являются дифракц. искажения, обусловленные
конечностью размеров линз. Влияние конечных размеров линз моделируется диафрагмой,
расположенной в фурье-плоскости оптич. системы (рис. 6) (диаметр диа-
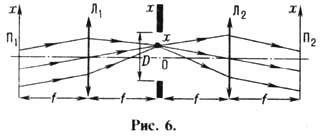
фрагмы D равен диаметру
меньшего из объективов). В формировании изображения в такой модели принимают
участие лишь те плоские волны, к-рые фокусируются линзой
Л1 внутрь диафрагмы, т. е. волны с пространств. частотами
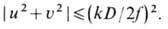
Эти волны приходят к плоскости
изображения П2 без искажений по амплитуде и фазе. Все прочие волны,
задерживаясь диафрагмой, не достигают плоскости изображения, т. е. оптич. система
имеет частотную характеристику:
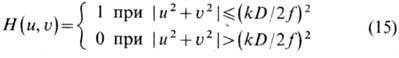
(т. н. дифракционно-ограниченная
система). функция рассеяния [обратное фурье-преобразование функции (15)] имеет вид
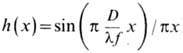(одномерный случай);
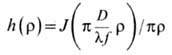(круглая диафрагма).
Принцип корреляционной
фильтрации. Т. к. плоские волны разных пространств. частот, фокусируясь
линзой Л1 в разные точки фурье-плоскости, пространственно разделяются,
то можно избирательно воздействовать на разл. пространств. гармоники. Если маленькую
пластинку-транспарант, вносящую определ. поглощение и (или) определ. фазовую
задержку, поместить в точку (х, у)фурье-плоскости, то эта пластинка
изменит амплитуду и (или) фазу только той плоской волны, к-рая в эту точку фокусируется
(т. е. волны с частотой u= kx/f, u=ky/f). При этом все др. волны
достигают плоскость изображения без искажений по амплитуде и фазе. Помещая в
фурье-плоскость разл. маски-транспаранты, можно непосредственно влиять на пространств.
спектр изображения.
Маска с функцией пропускания
т(х,у), помещённая в фурье-плоскость, приводит к частотной характеристике
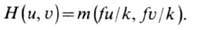
Метод управления частотной
характеристикой оптич. системы с помощью транспарантов, устанавливаемых в фурье-плоскости,
наз. принципом корреляц. фильтрации. С его помощью решаются разнообразные задачи,
такие, как улучшение разрешающей способности оптич. системы, связанное, напр.,
с сужением гл. максимума функции рассеяния; уменьшение боковых лепестков функции
рассеяния (апо-дизация), выполняемое с помощью т. н. мягких диафрагм- плавного
уменьшения пропускаемости диафрагмы от центра к краям (напр., по линейному закону);
устранение пространственно-периодич. шума в изображении; апостериорная обработка
изображений.
С помощью оптич. системы
можно совершать ряд ма-тем. преобразований. Для этого функция, подлежащая преобразованию
(в общем случае функция двух переменных), записывается в виде комплексной пропускаемости
транспаранта, к-рый располагается во входной плоскости. При освещении такого
транспаранта параллельным пучком лазера получаем на выходе транспаранта требуемое
поле f(x,y), преобразуемое затем в оптич. системе. Таким способом можно
проводить двумерное преобразование Фурье, операции свёртки и корреляции, дифференцирование
функций одной переменной с помощью частотной характеристики H(u) = iu [1]
и т. д. Многоканальный анализатор спектра, выполняемый с помощью комбинации
сфе-рич. и цилиндрич. линз, позволяет проводить одномерное преобразование Фурье
в большом числе каналов одновременно.
Преобразование пространственно-случайных (спекл-по-лей) в оптических системах. Из теории фильтрации случайных сигналов линейными колебат. системами хорошо известна связь между спектрами мощности (фурье-образами корреляц. функций) сигналов на входе и выходе фильтра Gk(w) = Fk(w)|H(w)|2, где H(w)-частотная характеристика фильтра. Аналогичное равенство справедливо для решения задачи фильтрации спекл-полей в оптич. (пространств.) фильтрах:
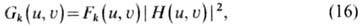
где Gk(u, u)и Fk(u, u) - пространств. спектры мощности
(фурье-образы автокорреляц. функций) спекл-полей во входной и выходной плоскостях
оптич. системы.
В соответствии с (16) управление
характеристиками системы для фильтрации спекл-полей осуществляется с помощью
амплитудных транспарантов.
Некогерентные оптические
системы. В некогерентных системах входным и выходным сигналами являются
интенсивности света Iвx (х, у)и Iвых
(х, у)во входной и выходной плоскостях. Связь между ними определяется
равенством
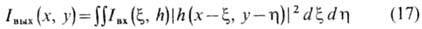
(при выполнении условия
изопланатичности).
Из (17) следует связь между
нормированными спектрами (фурье-преобразованиями) функций Iвх
(х, у)и Iвых (х, у):
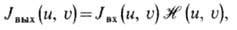
где Jвх(u,
u)и Jвых(u, u) -фурье-образы функций Jвх(x,
у)и Iвых(x, y);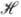 
(u, u)-п е р е д а т о ч н а я ф у н к ц и я оптич. системы, определяющая
свойства некогерентной оптич. системы.
Связь между когерентной
частотной характеристикой H (и, u)и передаточной функцией оптич.
системы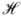 
(и, u)для одномерного случая имеет вид
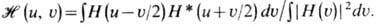
Возможности использования идей и методов Ф--о. существенно расширяются с применением динамически управляемых ячеек и транспарантов, располагаемых в фурье-плоскости оптич. системы: жидких кристаллов, ультразвуковых ячеек, эл--оптич. ячеек Керра и т. д.
Релятивисты и позитивисты утверждают, что "мысленный эксперимент" весьма полезный интрумент для проверки теорий (также возникающих в нашем уме) на непротиворечивость. В этом они обманывают людей, так как любая проверка может осуществляться только независимым от объекта проверки источником. Сам заявитель гипотезы не может быть проверкой своего же заявления, так как причина самого этого заявления есть отсутствие видимых для заявителя противоречий в заявлении.
Это мы видим на примере СТО и ОТО, превратившихся в своеобразный вид религии, управляющей наукой и общественным мнением. Никакое количество фактов, противоречащих им, не может преодолеть формулу Эйнштейна: "Если факт не соответствует теории - измените факт" (В другом варианте " - Факт не соответствует теории? - Тем хуже для факта").
Максимально, на что может претендовать "мысленный эксперимент" - это только на внутреннюю непротиворечивость гипотезы в рамках собственной, часто отнюдь не истинной логики заявителя. Соответсвие практике это не проверяет. Настоящая проверка может состояться только в действительном физическом эксперименте.
Эксперимент на то и эксперимент, что он есть не изощрение мысли, а проверка мысли. Непротиворечивая внутри себя мысль не может сама себя проверить. Это доказано Куртом Гёделем.
Понятие "мысленный эксперимент" придумано специально спекулянтами - релятивистами для шулерской подмены реальной проверки мысли на практике (эксперимента) своим "честным словом". Подробнее читайте в FAQ по эфирной физике.
|
|
 |
