
Фракталы - множества с крайне нерегулярной разветвлённой или изрезанной структурой. Термин "Фракталы"
предложен Б. Мандельбротом (В. Mandelbrot) [1], хотя подобные объекты изучались
в математике с кон. 19 в. Простейшим примером Ф. является канторово множество,
к-рое строится следующим образом. Из отрезка [О, 1] выбрасывается центр. часть
длиной 1/3. Из полученных двух отрезков [0, 1/3] и [2/3,
1] также выбрасываются центр. части, составляющие 1/3
длины отрезков, и т. д. В пределе получается нигде не плотное множество, имеющее
мощность континуума и нулевую длину (меру Лебега). Процесс построения
канторова множества допускает многомерные обобщения. В двумерном случае единичный
квадрат разбивается на первом шаге на девять квадратов со стороной 1/3
и центр. квадрат выбрасывается. Затем та же процедура повторяется с каждым из
оставшихся квадратов. Полученный в пределе Ф. наз. ковром Серпинского (см. рис.,
показаны первые 3 этапа построения).

Осн. характеристикой Фракталов служит хаусдорфова, или фрактальная, размерность (ФР). По одному из определений
Ф. наз. множество, для к-рого ФР строго больше топологич. размерности (см. также
Топология ).ФР строится следующим образом. Рассматривается произвольное
покрытие x Ф. М конечным или бесконечным набором шаров {Oi} радиуса ri<e.
Размерность Ф. М наз. такое число d>=0, что при
 для всех
g>d и
для всех
g>d и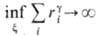 при e->0
при e->0 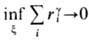 для всех g<d Можно
показать, что такое пограничное d существует и единственно. Для канторова множества
ФР d =ln2/ln3, а для двумерного ковра Серпинского d=ln8/ln3. Примерами естеств.
Ф. являются береговая линия материков и островов, снежинки, броуновские кривые
и т. д. Соответствующие ФР либо вычисляются, либо определяются экспериментально.
для всех g<d Можно
показать, что такое пограничное d существует и единственно. Для канторова множества
ФР d =ln2/ln3, а для двумерного ковра Серпинского d=ln8/ln3. Примерами естеств.
Ф. являются береговая линия материков и островов, снежинки, броуновские кривые
и т. д. Соответствующие ФР либо вычисляются, либо определяются экспериментально.
Большой интерес к Фракталам в физ. литературе связан с тем, что Фракталы возникают в реальных физ. задачах, причём в типичных, а не экзотич. ситуациях. Наиб. часто Фракталы встречаются в задачах нелинейной динамики, гидродинамики, статистич. механики, и в частности в теории фазовых переходов, в теории полимеров, в хим. кинетике и др.
В нелинейной динамике Фракталов возникают как аттракторы у диссипативных динамических систем. Аттракторами
наз. множества в фазовом пространстве, притягивающие траектории динамич. системы.
При этом, если аттрактор является Фракталом, его наз. странным аттрактором. Существование
странных аттракторов является типичным свойством диссипативных динамич. систем.
В случае дискретных отображений примером может служить аттрактор Фейгенба-ума
(см. Фейгенбаума универсальность). Хорошо изучен механизм образования
и свойства аттрактора Лоренца (Е. Lorenz), отвечающего системе ур-ний Лоренца
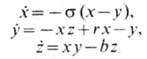
при значениях параметров
r=28, b=8/3, s=10[2]. Локально аттрактор
Лоренца имеет структуру прямого произведения канторова множества на двумерную
плоскость (т. н. книга Лоренца). Наиб. важным примером фрактальных аттракторов
являются странные аттракторы, возникающие в ур-ниях Навье - Стокса ([3], [4]).
Примером Фрактала в статистич. механике может служить критич. бесконечный проводящий кластер, возникающий в
задачах протекания теории. В наиб. характерных случаях проводящий кластер
состоит из связного набора рёбер d-мерной целочисленной решётки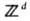 ,
поэтому определение ФР, данное выше, требует уточнения, к-рое делается следующим
образом. Введём число рёбер N(R)кластера, находящихся внутри шара радиусом
R. Тогда N(R)~const Rv где константа
v и выбирается в качестве ФР или размерности подобия. Значение v
зависит от размерности решётки d и определяется численно:
,
поэтому определение ФР, данное выше, требует уточнения, к-рое делается следующим
образом. Введём число рёбер N(R)кластера, находящихся внутри шара радиусом
R. Тогда N(R)~const Rv где константа
v и выбирается в качестве ФР или размерности подобия. Значение v
зависит от размерности решётки d и определяется численно: 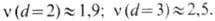 Отдельно изучают остов или "скелет" проводящего кластера, т. е.
ту часть кластера, по к-рой течёт ток (отбрасываются "мёртвые концы").
ФР v1 "скелета" бесконечного кластера
также определяется численно:
Отдельно изучают остов или "скелет" проводящего кластера, т. е.
ту часть кластера, по к-рой течёт ток (отбрасываются "мёртвые концы").
ФР v1 "скелета" бесконечного кластера
также определяется численно: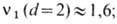
v1(d=3)=2[5].
Своеобразные Ф. возникают
в теории агрегации. В простейшей ситуации процесс агрегации можно описать так:
в начале координат решётки  помещается затравочная частица, к к-рой прилипают др. частицы, броуновски блуждающие
по решётке. Прилипшие частицы приклеивают к себе новые частицы и т. д. В результате
такого процесса возникает сильно разветвлённый фрактальный кластер - дендрит.
В каждый момент времени дендрит конечен, однако его ФР можно определить с помощью
асимптотики M(R)~constRv2, где М-число
частиц дендрита, находящихся внутри шара радиусом R. Численные эксперименты
дают значения
помещается затравочная частица, к к-рой прилипают др. частицы, броуновски блуждающие
по решётке. Прилипшие частицы приклеивают к себе новые частицы и т. д. В результате
такого процесса возникает сильно разветвлённый фрактальный кластер - дендрит.
В каждый момент времени дендрит конечен, однако его ФР можно определить с помощью
асимптотики M(R)~constRv2, где М-число
частиц дендрита, находящихся внутри шара радиусом R. Численные эксперименты
дают значения 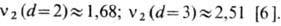
Все рассмотренные выше
Ф. обладают определ. свойствами масштабной инвариантности (скейлингом).
Так, кан-торово множество и ковёр Серпинского можно представить в виде объединения
соответственно двух и восьми подмножеств, линейные размеры к-рых в 3 раза меньше
размеров исходных множеств. Заметим, что в случае, когда множество разбивается
на N подмножеств, каждое из к-рых в R раз меньше всего множества,
ФР d=lnN/lnR. В этой ситуации скейлинговая структура определяется
одним масштабным множителем R. Однако в большинстве реальных случаев
масштабные множители неоднородны, т.е. во Ф. имеется целый спектр скейлингов.
Такие Ф. наз. мультифракталами. Типичным примером является аттрактор Фейгенбаума.
Обычно мультифракталы характеризуют спектром размерностей f(a) определяемым
следующим образом [7 ]. Рассматривается покрытие x Ф. М набором N шаров радиусом ri, 1<=i<=N. Вначале
определяются функция
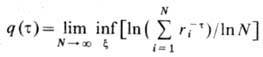
и обратная функция t=t(q).
Спектр размерностей f(a) является преобразованием Лежандра от функции t(q),
т. е.
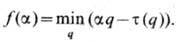
Макс. значение f(a) совпадает с ФР множества.

К. М. Ханин.
Когда тот или иной физик использует понятие "физический вакуум", он либо не понимает абсурдности этого термина, либо лукавит, являясь скрытым или явным приверженцем релятивистской идеологии.
Понять абсурдность этого понятия легче всего обратившись к истокам его возникновения. Рождено оно было Полем Дираком в 1930-х, когда стало ясно, что отрицание эфира в чистом виде, как это делал великий математик, но посредственный физик Анри Пуанкаре, уже нельзя. Слишком много фактов противоречит этому.
Для защиты релятивизма Поль Дирак ввел афизическое и алогичное понятие отрицательной энергии, а затем и существование "моря" двух компенсирующих друг друга энергий в вакууме - положительной и отрицательной, а также "моря" компенсирующих друг друга частиц - виртуальных (то есть кажущихся) электронов и позитронов в вакууме.
Однако такая постановка является внутренне противоречивой (виртуальные частицы ненаблюдаемы и их по произволу можно считать в одном случае отсутствующими, а в другом - присутствующими) и противоречащей релятивизму (то есть отрицанию эфира, так как при наличии таких частиц в вакууме релятивизм уже просто невозможен). Подробнее читайте в FAQ по эфирной физике.
|
|