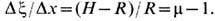
Томография. РЕАЛЬНАЯ ФИЗИКА. Глоссарий по физике

Томография (от греч. tomos - сечение, слой) - метод исследования внутр. структуры разл. объектов (промышленных изделий, минералов, биол. тел и др.), заключающийся в получении послойных изображений объекта при облучении его рентг. лучами, ультразвуком или др. излучениями. Соответственно различают рентгеновскую томографию (радиационную), ультразвуковую, оптическую, магниторезонансную томографию и др.

Техника получения изображений отд. слоев пространственных объектов разнообразна. Существуют методы продольного, поперечного, панорамного, симультанного томографирования с разл. вариантами проекц. облучения объектов. Особенно совершенное изображение получают в компьютерной (вычислительной) томографии.

При томографич. регистрации изображения к--л. слоя объекта источник излучения (напр., рентг. трубка) движется прямолинейно или по кругу в плоскости X₀, параллельной регистрируемому слою X₁, над объектом. Регистрирующий материал, обычно фотоплёнка, движется позади объекта в плоскости X₂, также параллельной плоскости движения источника, по аналогичным (подобным) траекториям, но в обратном направлении. Этим достигается стабилизация положения изображения регистрируемого слоя на фотоматериале, с одновременным размазыванием очертаний др. слоев.

Интересна возможность одноврем. получения изображений мн. параллельных слоев объекта (тела) на ряде фотоплёнок, расположенных одна над другой. Такой метод регистрации наз. симультанным. Симультанная томография открывает возможность отображать в объёмной регистрирующей среде полное трёхмерное теневое изображение объекта, просвечиваемого рентг. лучами.

Принципиальная схема симультанного томографа показана на рис. 1. Точечный источник излучения S(x, z = 0) находится в плоскости X₀(Z = 0). Точка объекта A(x = 0, Z=R)лежит в плоскости X₁, удалённой на расстояние R от X₀ (z = R), на оси OZ, нормальной к обеим плоскостям X₀ и X₁. Теневое изображение точки А точка A'(-x, z=H) лежит в плоскости X₂(z = H), удалённой на расстояние H от X₀ и тоже нормальной к оси OZ.

Для того чтобы при перемещении источника S на величину Dx изображение точки объекта А проецировалось на прежний участок регистрирующей среды, её нужно передвинуть на расстояние Dx в сторону, противоположную направлению движения источника. Обозначив H/R=m, из проекц. соотношений имеем: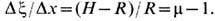

Соотношение скоростей движения источника излучения u₀ в плоскости X₀ и движения регистрирующей среды u₂ в плоскости X₂ должно быть: u₂=-u₀(m-1).

Величина m показывает также масштаб регистрируемого изображения A'D' относительно размера объекта AD. Из геом. соотношений, представленных на рис. 1, очевидно, что для точки В справедливы такие же соотношения, как и для точки А, т. е. масштаб томографич. изображения в продольном направлении

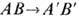таков же, как и в поперечном, т. е. получаемое объёмное изображение A'B'C'D' оказывается ортоморфичным объекту ABCD и увеличенным в m раз.

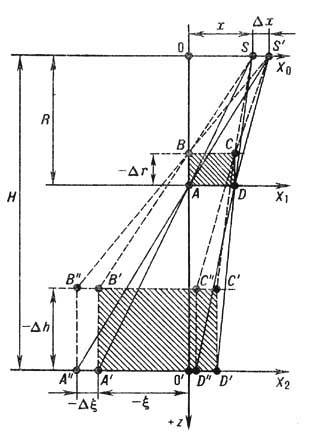
Рис. 1. Принципиальная схема симультан-ной томографической записи.

В качестве объёмной регистрирующей среды можно использовать, напр., многослойный набор фотоплёнок, заключённых в общую кассету и расположенных любым образом. Напр., как показано на рис. 2, слои фотоплёнок 1',2',3' могут быть расположены наклонно к направлению движения кассеты. В этом случае на плёнках будут симуль-танно (одновременно) зарегистрированы изображения, соответствующие косым сечениям объекта 1, 2, 3.

Кинематическая схема осуществления проекционной томографии возможна в 3 вариантах. Первый вариант, описанный выше, заключается в том, что просвечиваемый объект стоит неподвижно, а движется источник облучения и в противоположном направлении перемещается регистрирующая среда. Второй вариант может быть осуществлён с неподвижной регистрирующей средой и перемещающимися источниками и объектом. Третий вариант возможно осуществить с неподвижным источником и перемещающимися объектом и регистрирующей средой.

При обработке на ЭВМ, сравнивая оптич. плотности томографич. изображений смежных слоев объекта, можно на изображении регистрируемого слоя в значительной мере ослабить паразитные засветки и тени от структурных элементов др. слоев объекта и выделить слабоконтрастные детали регистрируемого слоя.

Применяя в качестве регистрирующей среды флюорес-центный экран и используя телевизионную систему для ввода изображения в ЭВМ, можно, последовательно перемещая экран по глубине томографич. изображения, непосредственно наблюдать на экране дисплея глубинное строение регистрируемых объектов.

Компьютерная томография

Компьютерная томография основана на том, что при просвечивании рентг. излучением объекта со сложной внутр. структурой информация об этой структуре может быть восстановлена по вычислению пространственного распределения интенсивности излучения, прошедшего через объект. Для получения картины распределения вещества в тонком слое тела просвечивают данное сечение тела пучками параллельно или веерообразно идущих коллими-рованных рентг. лучей, проходящих через исследуемый слой с разных сторон. В каждом из последоват. положений измеряется интенсивность излучения, прошедшего сквозь контролируемый слой, с помощью детекторов, расположенных по периферии контролируемого сечения объекта. Измерения интенсивности излучения подаются в память ЭВМ, где накапливается массив данных, по к-рым затем вычисляются коэф. ослабления излучения или значения плотности материала (вещества) объекта во всех ячейках сетки, образованной пересечениями разнонаправленных лучей в данном слое. По рассчитанным коэф. ослабления излучения на экране дисплея компьютером формируется двумерное полутоновое изображение исследуемого сечения объекта.

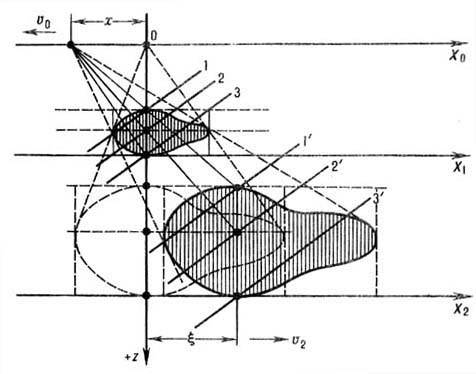
Рис. 2. Многослойная регистрация объёмного томографического изображения.

Задача реконструкции изображения состоит в нахождении двумерного распределения линейного коэф. ослабления излучения m(x, y) по известным экспериментально измеренным оценкам набора одномерных проекций (лучевых сумм вдоль прямых линий) p(r, j). Эта задача формально сводится к решению интегрального ур-ния для нормализованной величины линейной проекции вида

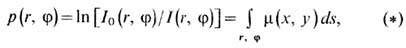
где координата каждого отдельного луча в проекции определяется как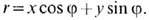

Здесь I₀ и I-интенсивности излучения, к-рые детектор измерил бы в отсутствие объекта и в его присутствии соответственно. На рис. 3 представлена система кооодинат при реконструкции двумерного распределения m(x, y) по известным параллельным проекциям p(r, j) Параллельным рядом прямых показано направление лучей от источника излучения S к детектору Д. Искомое распределение m(x, y) можно восстановить с необходимой точностью, используя известные алгоритмы, к-рые подразделяют на 2 осн. группы: алгебраические и аналитические.

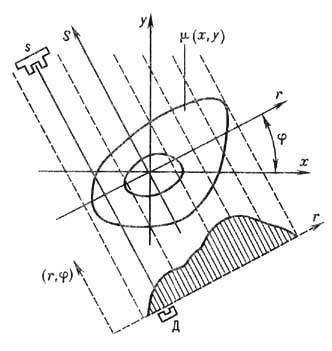
Рис. 3. Система координат при реконструкции плотности томографического изображения m (x,y) по известным параллельным проекциям.

В рамках алгебраич. методов распределение m(x, y) ищут в виде квадратной матрицы из n столбцов и n строк элементарных ячеек с постоянной, в пределах ячейки, рентг. плотностью m. Осн. ур-ние принимает вид:

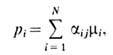
где a_ij-весовой коэф., отражающий вклад i-й ячейки в j-ю лучевую сумму; N- общее число ячеек в изображении (для круглого объекта).

Аналитич. методы реконструкции наиболее строги, они базируются на преобразованиях Фурье, обычно их разделяют на 2 группы, отличающиеся процедурой решения: двумерная реконструкция Фурье и обратная проекция с фильтрацией. В последнем случае применимы 3 разновидности фильтрации: Фурье, по Радону и свёрткой.

К достоинствам метода компьютерной томографии относится то, что томографич. изображение представляет объективное распределение величины линейного коэф. ослабления излучения по воспроизводимому сечению. Это создаёт предпосылки для автоматизации расшифровки результатов и анализа контролируемых объектов. Получаемое изображение данного сечения не имеет теней или помех от структур, неоднородностей и деталей, содержащихся в др. слоях объекта. Высокая точность измерений и вычислений позволяет при анализе изображений различать вещества и ткани, весьма мало отличающиеся друг от друга по плотности. Совр. средства компьютерной томографии обеспечивают пространственное разрешение 0,5-0,2 мм; продольное разрешение соответствует толщине слоя (обычно 5- 10 мм); разрешение по плотности контролируемого вещества (тканей) доведено до 0,1%.

Литература по томографии

Знаете ли Вы, что электромагнитное и другие поля есть различные типы колебаний, деформаций и вариаций давления в эфире.

Понятие же "физического вакуума" в релятивистской квантовой теории поля подразумевает, что во-первых, он не имеет физической природы, в нем лишь виртуальные частицы у которых нет физической системы отсчета, это "фантомы", во-вторых, "физический вакуум" - это наинизшее состояние поля, "нуль-точка", что противоречит реальным фактам, так как, на самом деле, вся энергия материи содержится в эфире и нет иной энергии и иного носителя полей и вещества кроме самого эфира.

В отличие от лукавого понятия "физический вакуум", как бы совместимого с релятивизмом, понятие "эфир" подразумевает наличие базового уровня всей физической материи, имеющего как собственную систему отсчета (обнаруживаемую экспериментально, например, через фоновое космичекое излучение, - тепловое излучение самого эфира), так и являющимся носителем 100% энергии вселенной, а не "нуль-точкой" или "остаточными", "нулевыми колебаниями пространства". Подробнее читайте в FAQ по эфирной физике.